感悟高考 突破高考 引领高考
——2014年安徽省数学高考理科第18题阅卷感悟
●
(淮北市第一中学 安徽淮北 235000)
1 背景分析
2014年6月10日~19日,笔者有幸参加了安徽省网上阅卷工作,所阅的是数学理科卷第18题(即文科卷第20题).从阅卷结果来看,本题安徽省理科平均分约4.5分,文科约2.1分.在阅卷之余,笔者思考:面对这样的答题情况,教师该如何教学?由此,笔者对学生的答题情况进行了分析,并把学生所犯的错误进行了归纳,以期为我们的教学提供借鉴与帮助.
2 试题回顾
例1设函数f(x)=1+(1+a)x-x2-x3(其中a>0).
(1)讨论f(x)在其定义域上的单调性;
(2)当x∈[0,1]时,求f(x)取得最大值和最小值时x的值.
(2014年安徽省数学高考理科试题第18题)
解(1)f(x)的定义域为(-∞,+∞),对f(x)求导得
f′(x)=1+a-2x-3x2.
令f′(x)=0,得

方法1可知f′(x)=-3(x-x1)(x-x2).当x
方法2对x,f′(x)和f(x)进行讨论(如表1所示):

表1 对x,f ′(x)和f (x)的分析
由表1可知:f(x)在(-∞,x1)和(x2,+∞)上单调递减,在(x1,x2)上单调递增.
(2)因为a>0,所以x1<0,x2>0.
①当a≥4时,x2≥1.结合第(1)小题知,f(x)在[0,1]上单调递增,从而当x=0时,f(x)取得最小值,当x=1时,f(x)取得最大值.

本题是函数与导数问题的综合题,紧扣考纲要求,主要考查了三次函数的图像与性质、导数运算及其应用、函数单调性及最值的求法,以及函数与方程的思想、转化化归的思想和分类讨论的思想.纵观安徽省近几年的考题,在函数与方程的考查中,多以有理函数、指数、对数函数、三角函数等有关的参数问题为主,考查导数在解决函数单调性、极值、最值等问题中的应用,注重基本思想和基本方法的考查.本题的难度不大,但是从阅卷情况来看,学生得分情况却不容乐观,主要在于求导不正确、计算与化简错误、审题不清等方面.
3 考生出现的错误及其分析
从阅卷情况来看,学生的错误主要有以下几种类型:
(1)方法性错误.
有的考生直接任取x1 (2)函数定义域求错. 有些考生受思维定式的影响,没有认真看题,见到a>0就误以为函数的定义域是(0,+∞),在判定函数单调性及解决第(2)小题时,把a的范围当成了R来讨论,于是就出现了对Δ=4+12(a+1)=12a+16进行讨论,这是学生审题不清所致.在平时的教学中,教师应该增强学生的审题意识.笔者在教学中发现总有一部分学生习惯于剪下题目贴到笔记本上,这其实是一种很不好的学习习惯.笔者认为记笔记时把题目手抄一遍有利于学生审题能力的培养. (3)求导错误. 常见的有以下几种错误求导方式: ①f′(x)=1+(1+a)-2x-3x2=2+a-2x-3x2; ②f′(x)=(1+a)-2x-2x2=1+a-2x-2x2; ③f′(x)=1+a-2x-3x=1+a-5x; ④f′(x)=1+a-x-x2; ⑤f′(x)=1+a-2x-x2; ⑥f′(x)=1+a-2x-3x2=-(3x2+2x+1-a); 等等. 本题考查了最常用的幂函数求导公式,并不难掌握,平时教学中也是经常强调,但学生仍然犯这种低级的错误:一方面是紧张的考试环境,导致学生思维“短路”;另一方面也给我们的复习指导找到了方向,这个方向就是高考前期要回归课本,要追本溯源,多看看教材中的基本概念、基本公式、基本定理以及知识的产生过程. (4)方程f′(x)=1+a-2x-3x2=0的根求错. 一些学生采用配方法解方程1+a-2x-3x2=0或不等式1+a-2x-3x2<0(>0),但是在配方时出现一些错误,常数配错或符号写反. 还有些考生对求根公式记忆模糊不清、公式代入错误、化简不正确等,比如阅卷中发现了以下结果: 化简时没有注意到正负号的变化规律. 代入公式时没有弄清楚二次项、一次项及常数项.若考生能够将方程式按照x的降幂排列,再代入公式,则可以避免该类错误. 错把二次函数顶点的纵坐标当成了求根公式. 化简时出错. 或 根的判别式代入错误. 从阅卷情况来看,相当一部分考生对最后的结果都没有化简,真正能把结论化简、问题完成的少之又少. 通过凡此种种的错误,我们发现:学生的基本运算能力有待于进一步提高,学生的思维能力相对于计算能力而言已经达到了一定的水平,制约学生得分的关键因素仍然是运算能力! (5)语言表述不规范. 值得说明的是,单调区间在x1,x2一端写成开区间或闭区间没有关系,写成f′(x)>0(<0)或f′(x)≥0(≤0)也不作追究. (6)单调区间求错. 单调区间写错的考生主要有2种类型: ①考生是把单调区间写反了,主要是因为考生在解不等式f′(x)<0时进行了以下的运算: 由f′(x)<0得 1+a-2x-3x2<0, 即 3x2+2x-(a+1)>0, 解得(-∞,x1)∪(x2,+∞).由于受到3x2+2x-(a+1)>0的影响,而忽视了前提是f′(x)<0,于是就得到递增区间为(-∞,x1)和(x2,+∞),同时得到递减区间为(x1,x2),这是学生解题习惯所致的错误. 负号写到分母上去了,这样x1就写成了x2! 由于第(1)小题的计算错误,使得很多考生在第(2)小题中的得分很低,甚至不得分.如在第(1)小题中,考生将f′(x)的2个零点写成 则得到当a>0时, 从而f(x)在x∈[0,1]上单调递增,这种情况下考生是得不到分的. 再如:有考生求导错误,求得f′(x)=2+a-2x-3x2,在接下来的做题中,思路和方法都和原问题相同,只是计算的数据错误,按照评分要求,考生只能得到思路分,很可惜. 一部分学生在第(1)小题正确解方程的基础上,也能够在第(2)小题中拿到一定的分数.这时犯错的考生主要表现在以下几个方面: ①讨论不够准确.没有注意到x1<0,x2>0,从而错误地对x1,x2与0的大小关系进行讨论. ③在回答问题时没有注意到题目所问.要求的是“取得最大值和最小值时x的值”,而不是函数的“最大值和最小值”! ④语言表述上不够规范.如f(x)取得最小值时x=1写成“xmin=1,f(x)取得最小值”或“最小值为f(1)min”. ⑤没有对a=1进行单独讨论. 还有些考生书写混乱:数学答题强调有理有据,但总有部分考生随心所欲,天马行空,书写没有层次感,严重缺乏逻辑性,不利于考生有条理地思考与解答,也不利于阅卷教师采分. 针对以上问题,笔者认为在日常教学中,教师要做到: (1)常规工作做扎实,查漏补缺.在平时的教学中,学生一听就会的问题,可以在习题课上板书1~2个题目,课后适当留下练习,让学生当作测验去做,及时认真批改作业,并根据学生做的情况,对于学生出错较多的问题集中点评. (2)给学生足够的时间与爱.对学生提出的问题及时解答,并与其一起讨论,激发学生对数学的求知欲及兴趣,为学生解疑答惑. (3)有效措施助力高考: ①回归课本.近几年安徽省的考题区分度较大,针对数学学科的特点,教师不可能靠猜题去打高考这场仗,而应该回归课本.这几年大纲强调课本,2013年、2014年的试题也充分反映了这一趋势.学校可以给每个教师配一套人教版和沪科版的教材,教师讲新课时,同步把课后一些较好的题目进行讲解. ②专项专攻.如晚自习之前利用一节课只考小题或只有大题,及时面改.这样学习的效果较好,或者尽量在晚自习前,找学生到办公室做几个题目,有利于提高学生的学习积极性和做题的正确率. ③大胆创新,引进先进经验.高中数学重在学生能力的培养,因此教师应该多教会学生如何分析问题、简化问题,讲课时可以让学生展示一下题目的思路. 另外,教师也可以自己大胆地创题,多走出去学习和交流. 总之,机会总是留给有准备的人.引领高考,需要我们做一个有理想、有目标、有胆识、勇于学习、努力钻研的有心人.


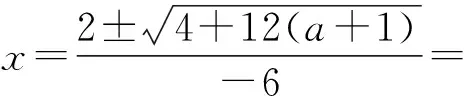
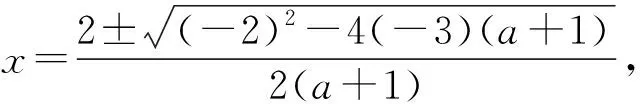



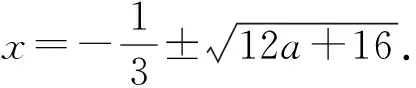




4 几点建议

