基于等效深度法的永磁涡流联轴器的涡电流分析与传递转矩计算
高庆忠,佟金锴,代 康
(1.沈阳工程学院 a.自动化学院;b.学报编辑部,辽宁 沈阳110136;2.太平湾发电厂 检修部,辽宁 丹东118000)
永磁涡流联轴器已广泛应用在发电企业的水泵和风机等设备上,该装置具有节能环保,免维护,安装方便,转矩传输效率高,抗负载冲击,震动小和软启动等特性。
永磁涡流联轴器通过导体盘产生的磁场与铜盘涡电流感应出的磁场进行场耦合以实现转矩的传递。其中,铜盘上的涡电流一部分产生感应磁场,作为磁传递转矩的动力,另一部分产生热量。因此,永磁涡流联轴器涡电流的准确计算及特征分析,为永磁涡流联轴器的设计提供了有效的理论依据。传递转矩的数学模型能反映出传动性能和相关参数之间的相互关系。因此,准确传递转矩数学模型可指导永磁涡流联轴器产品的改进和效率的提高。
1 永磁涡流联轴器的工作原理及结构
永磁涡流联轴器的结构如图1所示,主要由2个部分组成:一是连接电机的导体转子(铜盘),二是连接负载端的永磁转子(永磁盘)。导体转子与永磁转子间无任何连接可独立旋转,当电机带动导体转子旋转时,导体盘切割永磁转子中永磁体的磁力线,在导体表面产生涡电流,进而形成感应磁场,根据异性相吸、同性相斥的原理,相邻感应磁场对永磁体产生耦合力,这两种力在旋转方向上相叠加,在负载输出轴上产生转矩,从而带动负载做旋转运动。
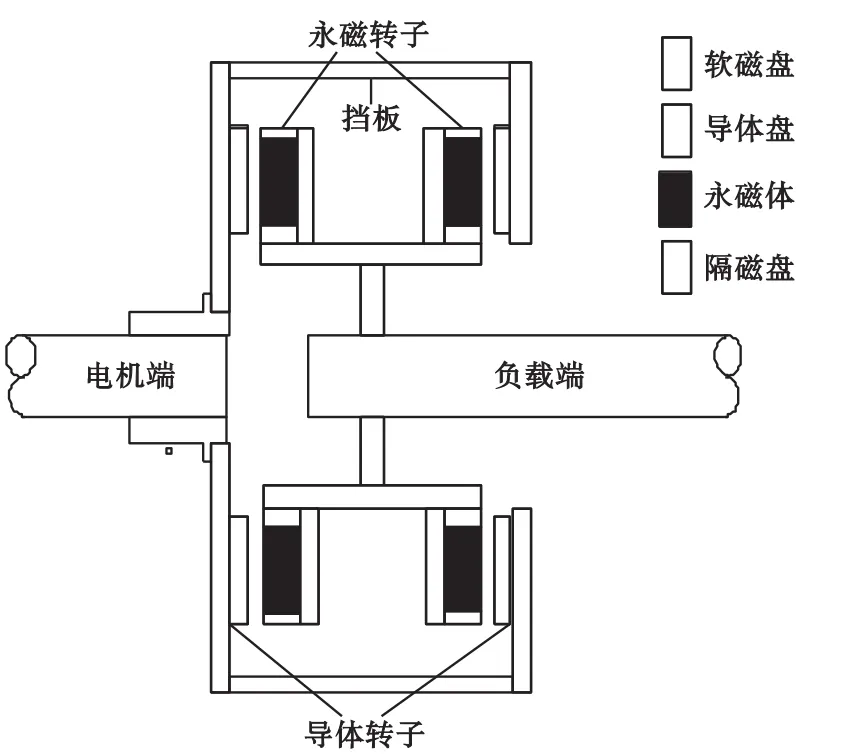
图1 永磁涡流联轴器的机械结构
2 涡电流密度的计算
2.1 涡电流分析
永磁涡流联轴器静止时,内部永磁体产生磁场。当电机带动铜盘转动时,铜盘做切割磁力线的运动,铜盘表面及一定深度内产生感应电动势,并产生涡电流。涡电流受集肤效应影响,使涡电流主要分布在铜盘的表层中。根据电磁学理论,涡电流的电流密度在轴向的分布是不均匀的,通常以等效透入深度Δh来表示,其等效透入深度的表达式为
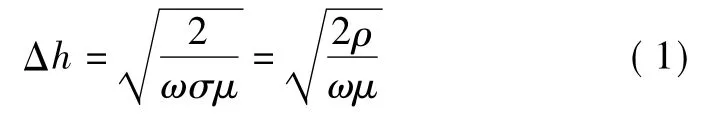
式中,μ = μ0μr,μ 为铜盘的磁导率,H/m;μr为铜盘的相对磁导率;μ0=4π×10-7H/m ,μ0为真空磁导率;ω=πnNp/30,ω为永磁体磁场变化的角频率;σ=1/ρ,σ为铜盘的电导率,s/m。
在研究永磁涡流联轴器铜盘表面的涡电流时,为简化计算,作以下假设:①仅考虑铜盘径向上的涡电流,且电流密度分布均匀;②电导率 σ和磁导率 μ为常数;③铜盘的磁滞损耗忽略不计,且所选用材料均匀同性;④仅考虑铜盘周向的磁感应强度变化;⑤忽略铜盘上的位移电流D和传导电流J;⑥忽略端部效应。
2.2 涡电流计算
按照上述假设在分析涡电流密度的分布时,采用直角坐标系(见图2)。铜盘径向用x轴表示,铜盘切向用y轴表示,铜盘轴向用z轴表示,电流正向为沿圆心指向外侧,反之为负。其中,h为铜盘的厚度,m;ωn为永磁盘和铜盘之间的相对角速度;B为转子盘表面处的磁感应强度,T;r1为铜盘内径、r2为铜盘外径,m;永磁盘和铜盘之间的相对转速为n,r/min。
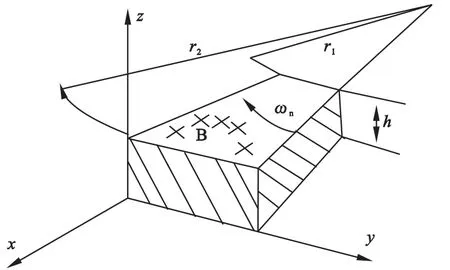
图2 涡电流密度分布
在计算涡电流密度时,由于不存在静止电荷,则麦克斯韦方程组可化简为以下形式
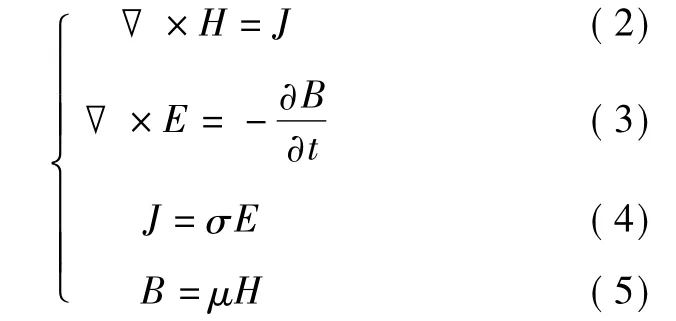
由假设可知,沿坐标轴方向的电磁场强度分量的麦克斯韦方程为
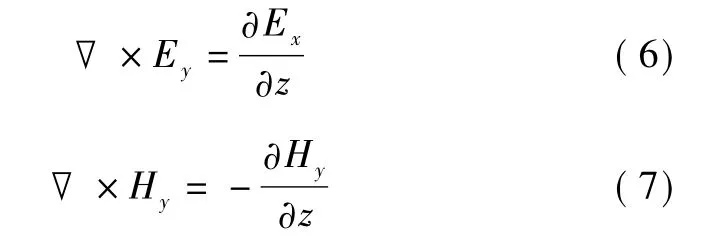
将式(6)代入式(2),式(7)代入式(3)得
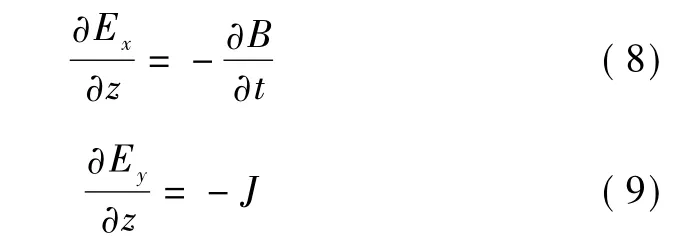
将式(5)代入式(8),式(4)代入式(9)得
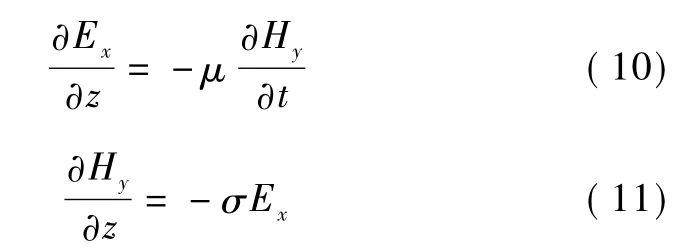
将式(10)对z取微分得
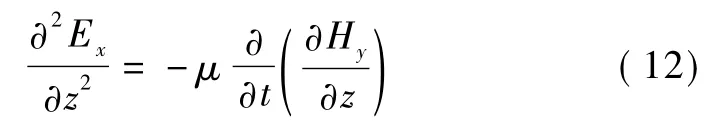
将式(11)代入式(12)得
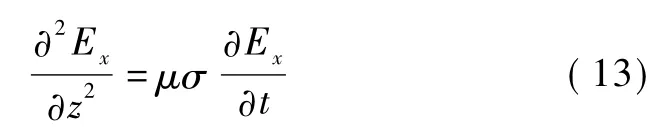
将式(11)对z微分得
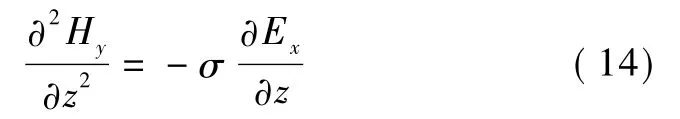
将式(10)代入式(14)得
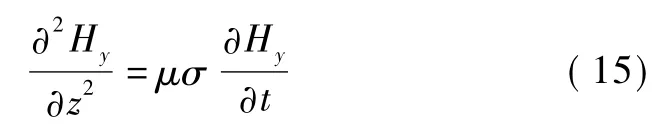
由假设可知,电磁场强度分量随时间按正弦波形式变化,故可用复数形式表示为
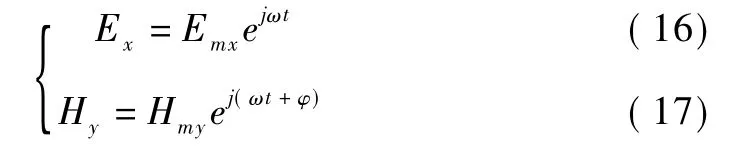
式中,φ为Ex与 Hy之间的相位差;ω=πnNp/30,ω为永磁体磁场变化的角频率。
将式(16)代入式(13)得

将式(17)代入式(15)得
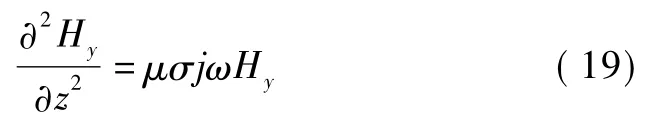
令 μσjw= λ2,则式(18)、(19)可化简为
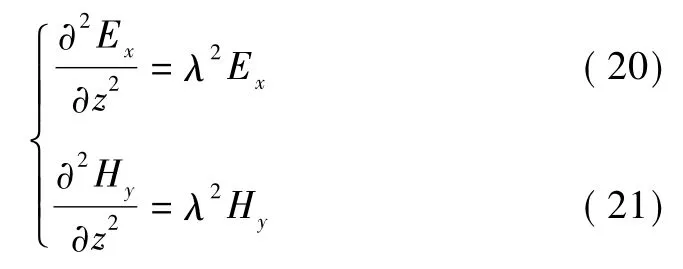
常系数方程组式(20)、(21)的通解为
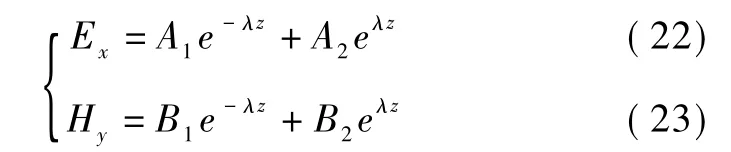
由于涡电流透入深度与铜盘厚度相比可忽略,则上式可简化为

式中,系数A1、B1可由铜盘表面处(z=0)的边界条件求出,得到铜盘表面处电场强度为E0,磁场强度为H0,可得到下式

由楞次定律,铜盘表面处电场强度E0为

式中,V=ωn(r2+r1)/2,为铜盘和永磁盘的相对线速度;由式(4)、(26)、(28)可得出铜盘的涡电流密度表达式为
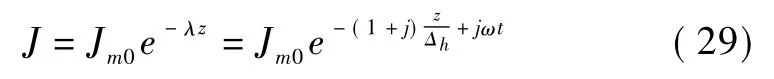
上式中,盘表面处涡电流密度幅值为

则涡电流的有效值为
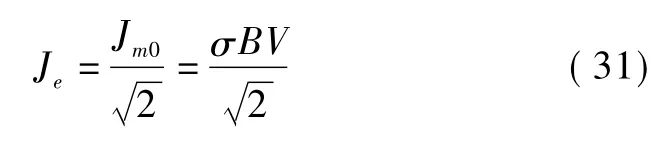
3 传递转矩的计算
取下限和上限分别为z=0、z=+∞,对式(29)沿铜盘轴向积分得到涡电流
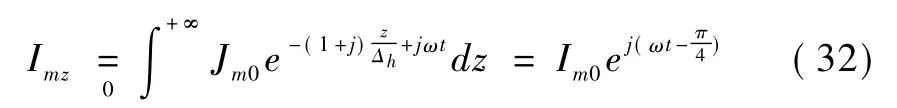
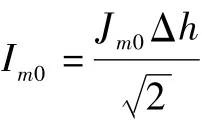
按照假设可以得到铜盘上所通过的涡电流的有效值Ie为
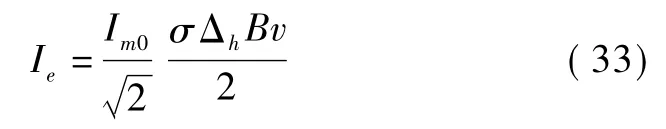
式中,v=ωnl,v为铜盘和永磁盘的相对线速度,m/s。根据假设主动轴相对于负载轴做匀速运动,所以铜盘上dθ弧度内涡电流 di为

式中,dθ为铜盘的周向微元,rad。
当涡电流产生退磁效应时,可得到盘间气隙中的磁感应强度为
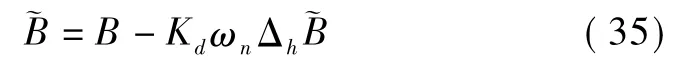
式中,Kd为线性关系的比例系数,取值范围为[1.12,1.65],将式(35)化简可得到气隙磁感应强度 ~B的表达式为
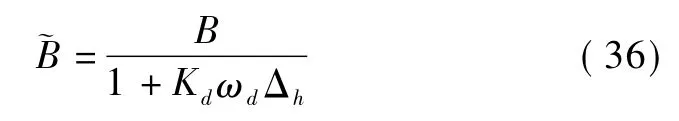
将式(36)代入式(33)可以求得磁感应强度 ~B所产生的涡电流的有效值Ie为
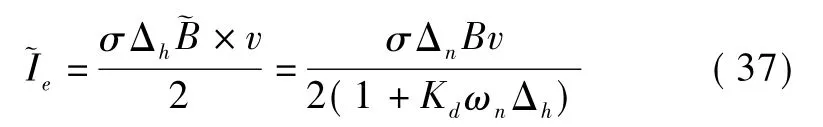
由安培定律,可以求得铜盘上dl段长度上所产生的安培力dF与磁传递转矩dT分别为

式中,dl为铜盘的径向微元,m;l为微元的的径向转矩,m;将式(34)、(38)代入式(39)得

对式(40)积分得到磁传递转矩T为
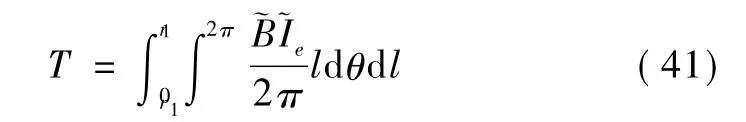
将式(36)、(37)代入式(41)并化简得
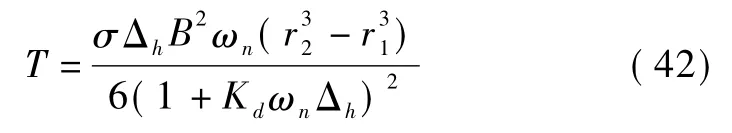
4 试验分析
试验台如图3所示,永磁体采用钕铁硼,性能参数为:剩余磁感应强度 Br为 1.294 T,矫顽力 HCB为1 529 kA/m,最大磁能积(BH)max为 318 kJ/m3,相对磁导率 μr为1.05。磁盘结构参数为:内径 R1为90 mm,外径R2为140 mm。驱动盘参数为:电导率 σ为1.408 5 ×107S/m,相对磁导率μ为0.999 99,内径r1为90 mm,外径r2为140 mm,厚度H为30 mm。输入相关技术参数 σ、r1、r2、B、Δh及工况相对转速 n,且线性关系的比例系数Kd取1.4,计算出传递转矩。测试永磁涡流联轴器输出转矩与转子转速的关系,并最终确定永磁涡流联轴器的最大转矩和临界转速。计算结果如图4所示。

图3 永磁涡流联轴器实验台
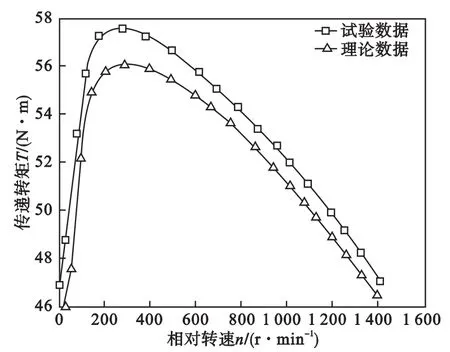
图4 永磁涡流联轴器试验与理论数据
从图4可以看出,在低转速的情况下,传递转矩随转速增大而增大,当转速达到临界转速后,随着转速的提高,传递转矩开始逐渐减小,这是因为铜盘上电涡流产生去磁效应所致。从图4还可以看出,计算值略小于试验值,产生原因是忽略了磁滞损耗、径向和切向的电涡流密度的影响。理论计算值与实验值虽存在一定误差,但误差在可接受的范围内,误差主要来源于理论分析中进行了相应的简化和假设,以及温度升高对材料磁导率和电导率的影响。
5 结论
1)分析了电涡流透入深度和涡流去磁效应,在此基础上推导了永磁涡流联轴器的涡流密度和传递转矩的计算公式,公式可以有效地反映出各参数之间的关系。
2)电涡流所产生的去磁效应影响了转矩的传递,铜盘与永磁盘相对转速越大,传递转矩越小。
3)影响计算值的因素较多,导致与试验值存在一定偏差,需要通过进一步试验研究来修正计算公式。所提出的计算方法可为永磁涡流联轴器结构设计和特性分析的提供依据。
[1] Wallace A,Von Jouanne A,Williamson S,et al.Performance prediction and test of adjustable,permanent-magnet,load transmission systems[C]//IEEE Industry Applications Conference 36th IAS Annual Meeting.Chicago,2001:1648-1655.
[2] Wallace A,Von Jouanne A,Ramme A,et al.A permanentmagnet coupling with rapid disconnect capability[C]//Proceedings of International Conference on Power Electronics Machines and Drives.Bath,2002:286-291.
[3] Smith A C,El-Wakeel A,Wallace A.Formal design optimization of PM drive couplings[C]//IEEE Industry Applications Society Annual Meeting.Pittsburgh,2002:205-211.
[4] Gholizad H,Mirsalim M,Mirzayee M.Motional eddy currents analysis in moving solid iron using magnetic equivalent circuits method[C]//IEEE/ACES International Conference on Wireless Communications and Applied Computational Electromagnetics.Honolulu,2005:535-538.
[5] Peng Ying,Ruan Jianqiun,Zhang Yu,et al.A composite grid method for moving conductor eddy-current problem[J].IEEE Transactions on Magnetics,2007,43(7):3259-3265.
[6] Wallace A,Wohlgemuth C,Lamb K.A high efficiency,alignment and vibration tolerant,couplerusing high energyproduct permanent magnets[C]//Seventh International Conference on Electrical Machines and Drives.Durham,1995:232-236.
[7] Wallace A,Von Jouanne A.Industrial speed control:are PM couplings an alternative to VFDs [J].IEEE Industry Applications Magazine,2001,7(5):57-63.
[8] Wallace A,von Jouanne A,Jeffreys R,et al.Comparison testing of an adjustable-speed permanent-magnet eddy-current coupling[C]//Proceedings of IEEE Pulp and Paper Conference.Atlanta,2000:73-78.
[9] Wang Xu,Wang Da-Zhi.Magnetic Circuit Structural Design of Permanent Magnetic Drive[J].ElectricDrive,2011,41(10):55-58.
[10] Wang Xu,Wang Da-Zhi,Liu Zhen.Eddy current field analysis and performance calculations for adjustable permanent magnetic coupler [J].Chinese Journal of Scientific Instrument,2012,33(01) :155-160.
[11]苏洪伟.永磁涡流联轴器性能分析[D].长春:吉林大学,2013.

