超高速磨床结构建模的研究

朱 爽

(沈阳工程学院机械学院，辽宁沈阳110136)

超高速磨削技术是指加工速度不低于150 m·s-1的磨削方法。由于加工速度的提高，使得超高速磨床具有磨削力小、磨削稳定、加工表面完整性好等优点，这使得零件的加工效率和表面质量有所提高，而且有助于实现磨削加工的自动化。超高速磨削加工方法使得磨削技术得以向难加工材料进行挑战。超高速磨削加工零件的精度与超高速磨床的整机动态性能密切相关，确保超高速磨床具有良好的动态性能是提高加工精度的必要条件。因此，在机床投入生产前要分析机床结构动态性能并积极改进机床的设计，而分析机床动态特性的首要任务是建立正确的动力学模型。

1 整机几何模型的建立

作为研究对象的超高速磨床由7大部分组成:床身、立柱、主轴箱、大工作台、小工作台、主轴和砂轮。对该超高速磨机床进行实地测绘，根据各部件的实际结构和尺寸在pro/E软件中进行三维CAD模型的建立。为了更好地对机床进行有限元分析，需要对CAD模型进行简化。化简时遵循以下原则:

1)模型尽量精确，以保证CAD模型能正确地反映结构特征和动、静态特性。

2)对于模型中的细小特征和影响较小的零部件可以忽略。

3)简化模型中的小锥度平面和小曲率曲面。

4)利用结构对称性进行建模。

完成所有部件的三维建模以后，对超高速磨床进行装配，获得超高速磨床的虚拟样机模型，如图1所示。

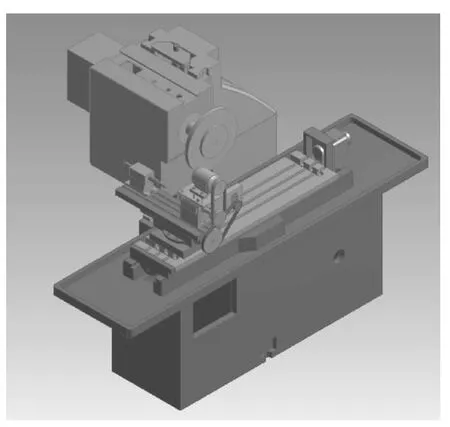
图1 超高速磨床CAD模型

2 结合部的建模

机械结构是由许多零件按照一定的功能要求组合起来的整体。2个零件间相互接触的部位称为结合部，其特性对机床结构的动态特性有很大的影响。研究表明，机床刚度中的60% ～80%来源于结合部，而机床总阻尼的来源更多，高达90%以上源于结合面。所以，研究机床动态特性的重点在于研究结合部的动力学特性。

2.1 等效动力学模型

机床结合面的相互接触可以视为无数个结合点的相互接触，因此在受到外力作用时，结合面处弹性和阻尼并存，储存能量的同时又消耗能量。考虑到结合面的上述特性，在建立结合部的等效动力学模型时是采用弹簧和阻尼器来组成等效果的结合部。等效后的结合部由3部分组成，如图2所示。

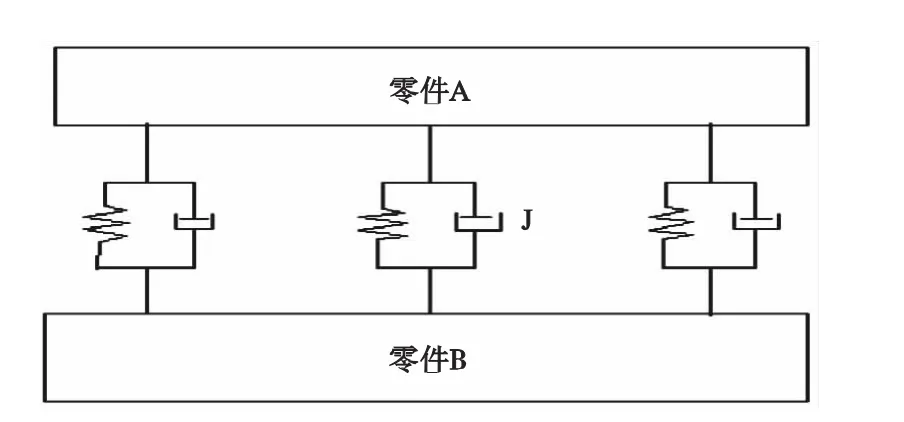
图2 结合部简化模型

其系统动力学方程可表示为

式中，Ma、Mb为零件的质量矩阵，Ca、Cb为零件阻尼矩阵，Ka、Kb为零件刚度矩阵，Cj、Kj分别是结合部J的阻尼矩阵和刚度矩阵，xa、xb为零件的坐标向量，也表示系统的坐标向量。

超高速磨床的主轴箱与立柱之间为矩形导轨结合部，主轴箱可以沿导轨做z方向移动，即对z方向移动自由度没有限制。分别用x方向和y方向的等效弹簧和阻尼器来等效矩形导轨结合部，其模型如图3所示。大工作台与床身之间为燕尾槽导轨结合部，大工作台可沿导轨做x方向的移动，即对x方向移动自由度没有限制。分别有y方向和z方向的等效弹簧和虚拟器来等效燕尾槽导轨结合部，其模型如图4所示。同理小工作台与底座之间的燕尾槽导轨结合部分别用x方向和z方向的弹簧和阻尼器来等效替代，如图5所示。

2.2 参数识别

确定了结合部的动力参数才能准确建立结合部的动力学模型，因此参数识别是必不可少的步骤。为了能够准确地识别参数，在很多参数识别方法当中，最常用的有理论计算法、试验测试法和理论建模与试验测试相结合的方法。

图3 主轴箱与立柱结合面等效结构

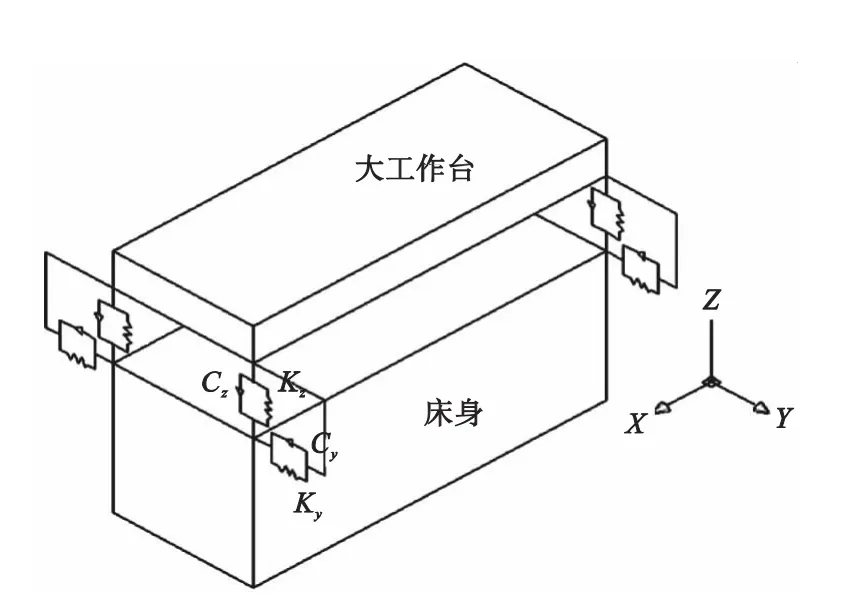
图4 大工作台与床身结合面等效结构

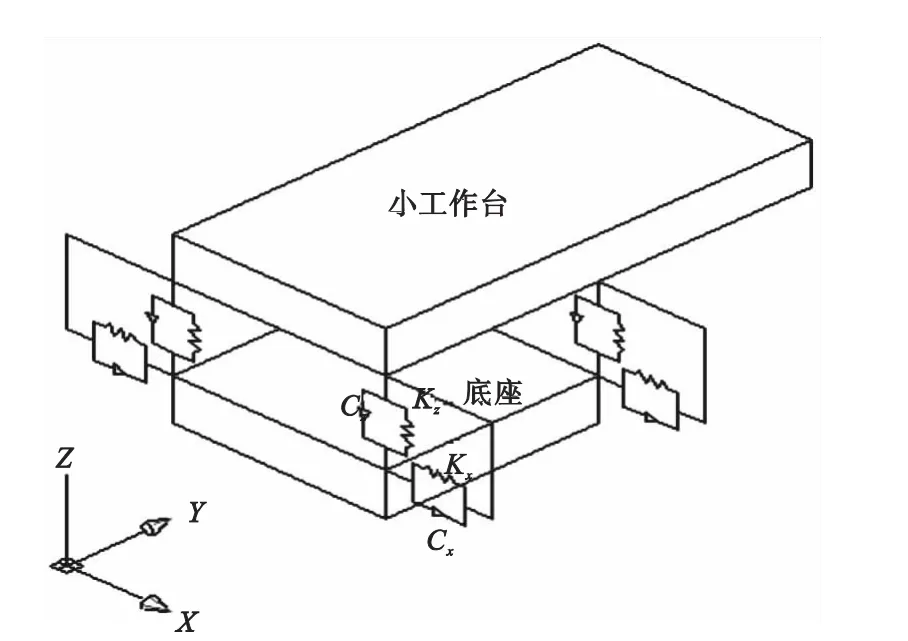
图5 小工作台图底座结合面等效结构

超高速磨床结合部的参数采用吉村允孝法来确定。吉村允孝法(结合面面积积分法)是吉村允孝通过测量结合部在结合条件不同时的等效刚度和等效阻尼，然后利用不同的结合条件、正压力下单位结合面面积上的刚度和阻尼计算出整个结合面在正压力下的刚度和阻尼的方法。这种方法可以将结合面的动态特性参数的研究简化为单位面积、相同条件的研究，降低了研究的难度。

吉村允孝的计算公式为

其中，Pn为结合面的法向压力;k1(Pn)为切向单位面积的等效刚度;k2(Pn)为法向单位面积的等效刚度;c1(Pn)为切向单位面积的等效阻尼;c2(Pn)为法向单位面积的等效阻尼。

压力分布均匀时上式可化简为

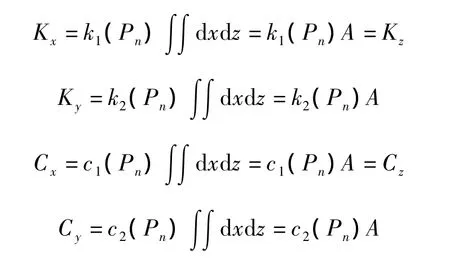
其中，A为结合面的面积。其计算结果如表1所示。

表1 超高速磨床主要结合部动力学参数表

3 有限元模型的建立

有限元模型建立的是否正确是分析结构动态特性和改进结构的基础。因为在Ansys软件中建立模型比较麻烦，所以在pro/E软件中对超高速磨床进行三维实体建模，再将建好的模型导入Ansys软件中进行网格划分。

在网格划分中，床身、立柱等实体采用实体单元solid187来划分，为了模拟结合面既有刚度又有阻尼的特点，导轨结合面采用弹簧阻尼单元sprin-damper14来划分。采用弹簧阻尼单元模拟结合面，首先在导轨的外表面及滑块内表面相应位置建立硬度，连接两个硬度建立直线，让后将直线划分为弹簧阻尼单元即可，如图6所示。其中每根直线只能划分为1个弹簧阻尼单元。

在划分网格过程中采用智能划分与手动划分相结合的方法，每个部件划分完网格后，对网格的单元质量进行了检查，及时修正质量不佳的网格，避免造成分析结构误差较大或计算失败的结果。与此同时，需要定义机床各部件的弹性模量、泊松比和密度，最后完成对超高速磨削平台的有限元模型建立，如图7所示。

图6 导轨滑块弹簧阻尼单元布置

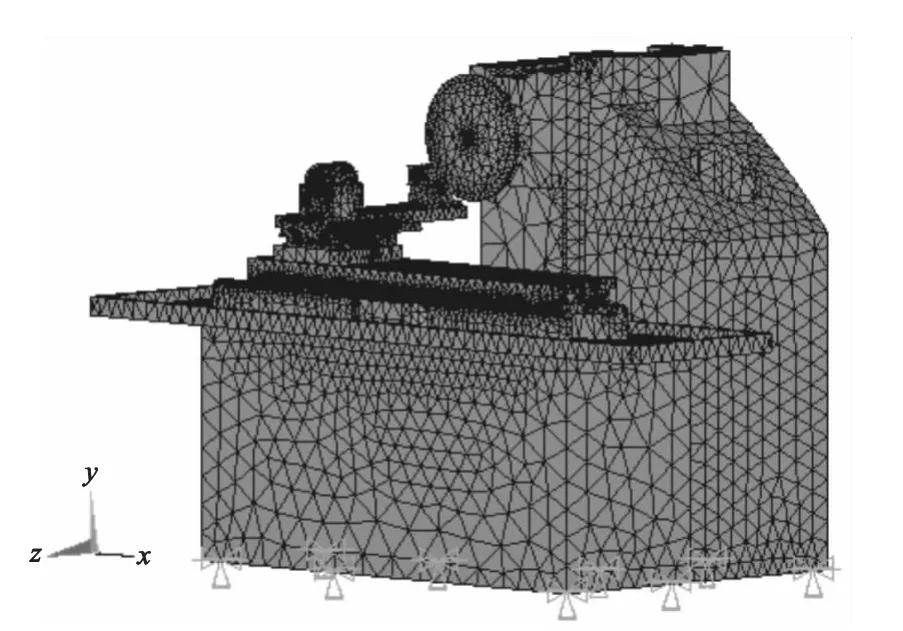
图7 超高速磨床有限元模型

4 整机模态分析

模态分析是近代研究结构动力特性的1种方法，是系统辨别方法在工程振动领域中的应用。模态分析的方法是通过模态参数来分析、预测、评价和优化其动态特性，其核心问题是解决多自由度系统运动方程组的内部耦合，及所谓的解耦。

1个具有粘性比例阻尼的自由度系统在1组激振力作用下，其运动微分方程为

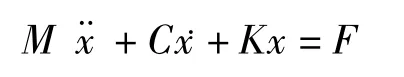
式中M是质量矩阵，C是阻尼矩阵，K是刚度矩阵，x是系统中各点的位移向量，F是各点的激励向量。

结构的固有频率只取决于结构本身的属性，不收外部载荷的影响;阻尼对结构的固有频率和振型影响不大，因此在分析过程中忽略阻尼的影响。上述结构的动力学方程简化为无阻尼自由振动方程为

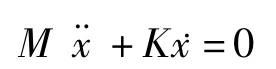
如果振动是简谐振动，方程式可简化为

模态分析选用 Ansys软件来运行，采用 Block Lanczos方法来提取分析结果。超高速磨床前22阶固有频率值如表2所示。

表2 模态分析结果

5 动态特性实验

实验测试流程如图8所示。

图8 测试流程

此实验采用的是锤击激振法，由于在实验过程中锤击位置、锤击力的大小、方向存在差异，以及周围环境造成的影响，导致该方法具有不可重复的特点。故在实验过程中，每次测量的实验结果都不完全相同。为了最大限度保证实验的准确性和合理性，采用多次测量的方法。超高速磨床4阶实验频谱如图9所示。

图9 超高速磨床4阶实验频谱

从表3可以看出，仿真分析所获得的固有频率与实验所得固有频率相近，可以认为超高速磨床的有限元分析方法合理，通过该方法分析机床的动态特性具有可靠性。

表3 有限元仿真与测试固有频率比较

6 结语

机床的加工精度与其动态特性密切相关，而机床建模是动力学研究中的关键，准确的建立模型有助于动力学研究。以超高速磨床为例建立模型过程，为机床建模提供了方法，为模态分析奠定了基础。

［1］朱从容.超高速磨削及其关键技术［J］.磨床与磨削，2000(4):51-52.

［2］孙燕华.超高速磨削技术［M］.北京:机械工业出版社，2010.

［3］ Schulz H，Wurz T.Balancing Requirements for Fast Rotating Tools and Spindle Systems.Annals of the CIRP，1998，47(1):321-324.

［4］于 洋，张建润，泸 熹，等.五轴联动加工中心主轴系统的结构优化［J］.精密制造与自动化，2006，166(2):23-25.

［5］张学良，温淑花，徐格宁，等.结合部切向接触刚度分形模型研究［J］.应用力学学报，2003(1):70-72.

［6］ Huang Yumei，Fu Weiping，Tong Junxian.A Method of Acquering Applied Tangential Damping Parameters of Joint Surfaces［J］.Jornal of Xi’an University，1996(1):1-5.

［7］李德葆，陆秋海.实验模态分析及其应用［M］.北京:科学出版社，2001.

［8］王学林，徐 岷，胡于进.机床模态特性的有限元分析［J］.机床与液压，2005(2):48-49.