节块法部分插棒显式表示法及数值结果
李志勇
(深圳中广核工程设计有限公司 上海分公司,上海 200030)
基于中子扩散横向积分技术的节块法经几十年的发展,演化出很多不同方法[1-2],如节块展开法(NEM)、解析节块法(ANM)、半解析节块法(SANM)。一般而言,基于横向积分方程的节块法其理论模型有一基本假设——节块内中子截面参数为常数。由于节块一般不大,这种假设在大多数情况下是有效的。但在某些情况下,如计算控制棒微分价值及控制棒相关动力学问题模拟等这类节块内截面随节块空间剧烈变化的问题,为满足上述基本假定一般采用体积权重均匀化,会出现数值结果明显发生偏差的情况,即锯齿效应[3]。
为缓解锯齿效应对节块法计算结果的影响,本文通过在横向积分方程中显式引入节块内随高度变化截面的方式,研究一种节块法显式表示法。
1 理论模型
1.1 中子截面分析
控制棒作为强吸收体,对燃料节块的分群中子宏观截面造成很大影响。一般而言,控制棒主要对吸收截面(特别是热群截面)有显著影响。表1列出典型PWR燃料组件中控制棒对中子截面的影响。由表1可见,控制棒插入对吸收截面的影响较大,对其他中子截面影响较小,如能谱的变化对裂变截面产生轻微的影响。
考虑到后续提出的方法模型要求,并基于控制棒对中子截面的影响,对扩散系数可不进行显式处理,即采用传统的体积权重(或体积通量权重)。因此,在显式模型中不对控制棒部分插入引起的对扩散系数的影响进行处理,这种处理方式也能使本文提出的显式表示方法在理论模型上避免过于繁杂。
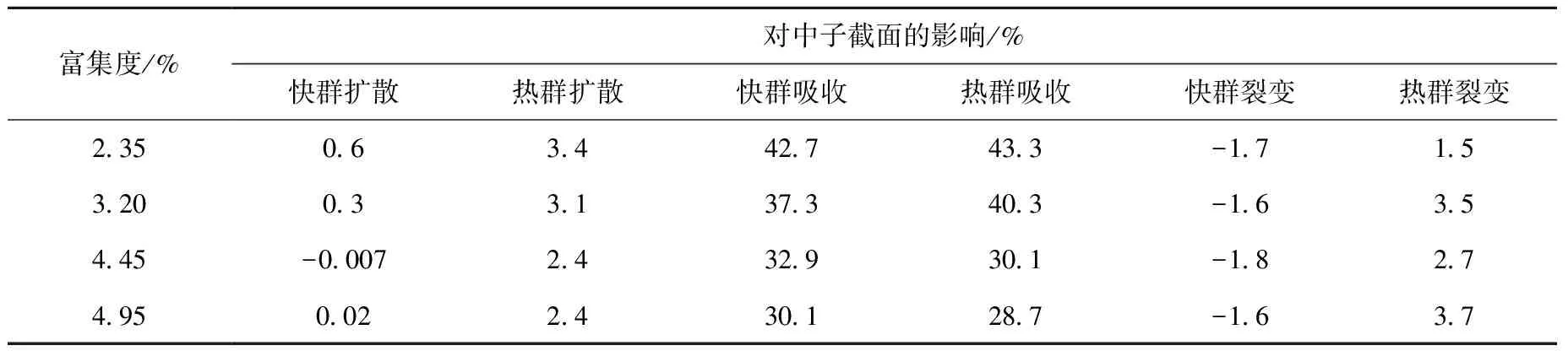
表1 控制棒对中子截面的影响
注:上述数值为典型值,具体数值与燃料组件类型有关
1.2 基本方程
基本中子扩散方程的积分形式为:
(1)
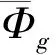
那么,中子扩散方程在u坐标方向上的横向积分方程为:
(2)
其中:Dg为中子扩散系数;φg为横向积分中子通量;Qg为横向积分中子源项;Lgu为中子横向泄漏。
由式(2)可看出,基于对中子截面的分析,在中子扩散方程横向积分方程的推导中,可显式地将控制棒部分插入引起的截面变化进行考虑,这将导致横向积分方程较一般情况下略复杂一些。
1.3 部分插棒截面表达
在节块法中部分插棒对节块中子截面产生影响(节块轴向影响)是一阶跃变化函数,且经处理后可进一步简化为阶跃函数。考虑到控制棒对中子扩散系数的影响非常小(实际上对除吸收截面外的其他截面影响均很小),因此可不考虑扩散系数的影响,且对其他截面的影响均移至方程右端(这可作为一额外源项附加到原一般源项上)。
因此,本文主要考虑部分插棒在轴向对节块吸收、散射和裂变中子截面的影响,具体部分插棒节块轴向中子截面阶跃函数的形式示于图1。图1中:p为控制棒归一化插入点,p=2u/Δu,p∈[-1,1];ΔΣ为由于控制棒插入导致的截面阶跃,即ΔΣ=Σrod-Σunrod,Σrod和Σunrod分别为插棒和不插棒部分中子截面相对于节块平均截面的差值。
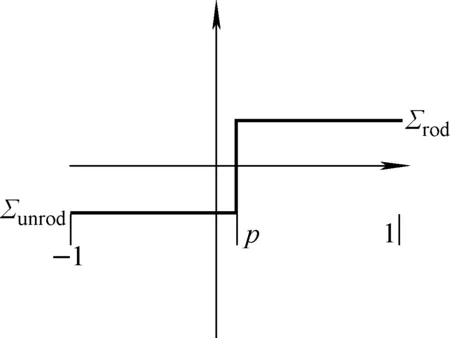
图1 部分插棒节块轴向中子截面表示
节块在轴向的截面可将部分插棒导致的与节块平均截面的差值分为两个部分:Bias项,该项即为不插棒部分截面相对体积(通量)权重平均截面的偏差,此项与轴向位置无关;Delta项,该项即为与轴向位置相关的截面随高度的变化(同时考虑减去Bias项后的截面),可认为是一个阶跃函数。
控制棒部分插入节块的中子截面可由式(3)表示:
ΔΣx=Σx-Σx,avg=
(3)
其中:Σx,avg为节块平均截面,下标x表示吸收、散射或裂变中子截面;h为节块轴向归一化高度;Σx,rod、Σx,unrod分别为含控制棒节块部分和不含控制棒节块部分的中子截面。
1.4 节块法模型
由于将部分插棒节块内中子截面表示为与平均中子截面的差值形式,因此原模型中包括的横向积分通量和基本公式还是适用的,这里仅需考虑部分插棒对横向积分方程的影响。考虑阶跃变化函数后,原通量展开函数失去正交性(但Bias项还具有正交关系),需较为繁琐的推导。
对于轴向,考虑具有非均匀截面后,节块内分群中子扩散方程可写为:
-DgΔφg+ΣR,g(h)φg=Qg
(4)
其中,φg、φg′为中子通量。
可发现,式(4)与一般节块法方程类似,因而一般方程的中子平衡方程和横向积分方程均可沿用,只是中子截面是与轴向位置有关的函数,因此在积分过程中复杂一些。这里考虑与位置有关的中子截面,并作为额外的源附加到横向积分方程的右端,称该源项为非均匀截面源,其具体形式为:
(5)
其中:φg为横向积分(展开)中子通量;QXS为非均匀截面源。
显然,由于考虑阶跃函数后权重函数不再正交,那么在原方程基础上将产生附加项(包括0~2次矩方程),这就需显式的求解。这里按一般勒让德多项式节块展开法为例给出各阶对区间[p,1]的积分结果,以便为后续横向积分方程附加非均匀截面源。需说明的是,符号“〈 〉”表示在区间上的积分。
0次矩为:
1次矩为:
2次矩为:
其中,W为展开函数。
由于与Bias项相关的源项与一般节块法的源项无区别,因此这里重点考查Delta项引起的源项(非均匀截面源)。基于上述权重函数在区间[p,1]积分结果给出该项的表示形式,可发现仅需要将附加的非均匀截面源附加到原各阶源项上即可,具体形式示于式(6):
(6)
需要说明的是,上述的理论推导不限于特定节块法横向积分中子通量展开形式,具有一定的通用性,即同样适用于半解析节块法。
1.5 动力学模型
基于文献[4]的刚性限制方法,研究显式表示方法在动力学中的应用。基本的三维动力学扩散方程为:
(7)
其中:vg为中子速率;β为缓发中子份额;χp,g为瞬发中子裂变谱;i为缓发中子群;Ci为缓发中子先驱核;λi为衰变常量。
假定:
则动力学方程可转化为如下形式:
其中:
其中,DG为缓发中子的群。
可看出,本文提出的控制棒部分插入显式表示方法由于未破坏原有的堆芯三维节块几何划分,动态频率还可依照原方法进行计算,因而上述刚性限制法还是适用的。采用刚性限制法结合控制棒部分插入显式表示方法,进行基准问题的数值计算并验证本文提出方法的有效性。
2 数值结果
2.1 IAEA 3D基准问题
IAEA 3D基准问题[3]是一广泛用于验证堆芯扩散问题的基准问题,它是一典型PWR问题,堆芯内成分复杂,包括调节控制棒和停堆控制棒。轴向和径向含有水反射层,外边界条件为真空边界。由于堆芯含有控制棒,可采用该基准问题计算控制棒微分价值并进行验证。
采用1/4堆芯位于(3,3)组件位置的一束控制棒(整个堆芯共计4束)计算控制棒微分价值随堆芯高度的变化,具体数值结果示于图2。其中:参考解结果为采用轴向节块宽度为1 cm进行的计算;体积权重法结果为采用一般体积权重法计算含有部分插入控制棒的节块平均截面并进行节块计算,且轴向节块宽度为20 cm;显式表示法的轴向节块宽度仍为20 cm。
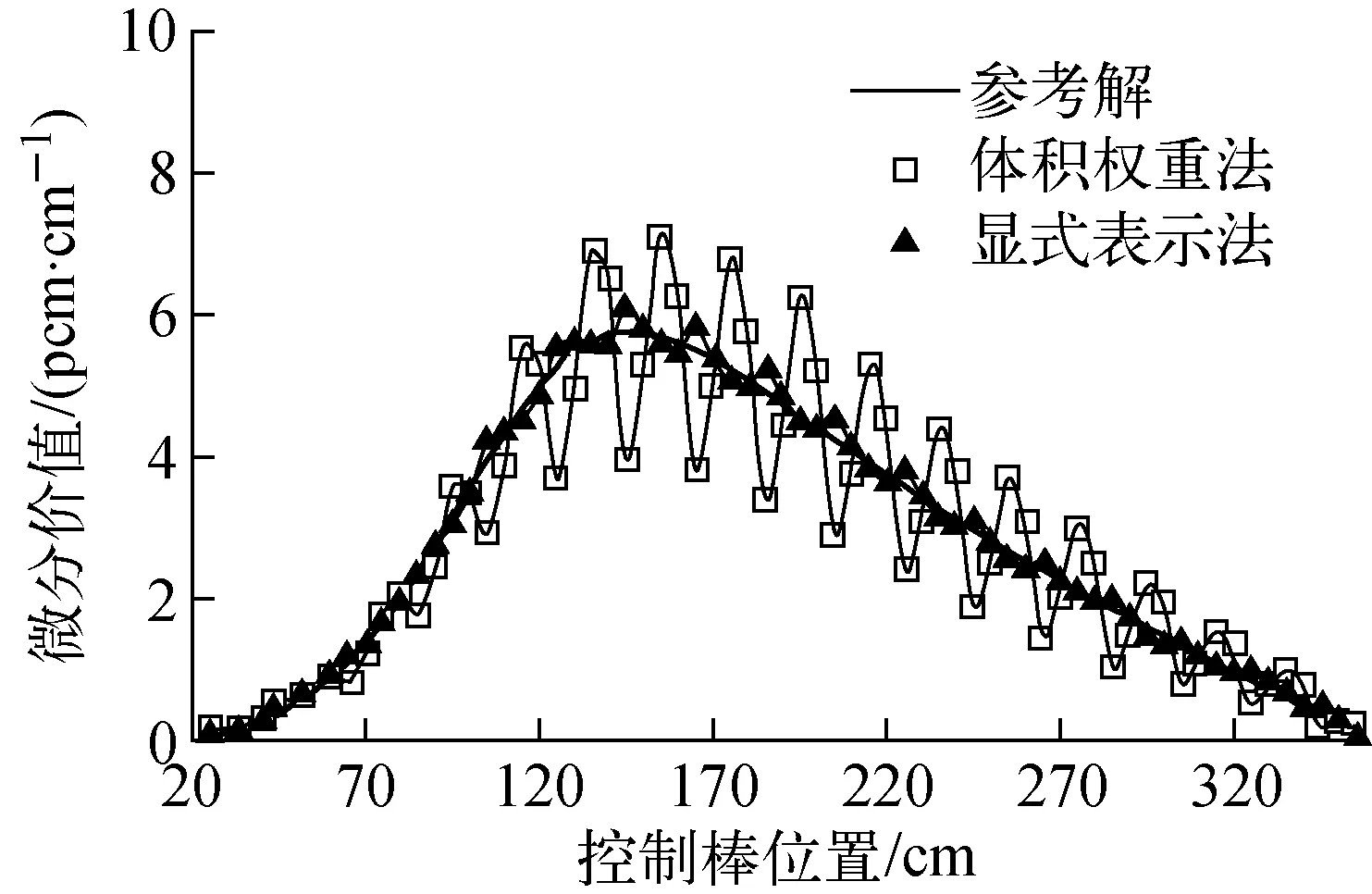
图2 IAEA 3D基准问题控制棒微分价值
从图2可见,显式表示法大幅缓解了锯齿效应带来的对于控制棒微分价值的影响(即体积权重法相对于参考解的偏差),基本达到工程应用的要求。
2.2 LMW三维瞬态基准问题
LMW三维瞬态基准问题[3]是一高度简化的压水堆瞬态问题,堆芯内共有77个燃料组件,组件尺寸为20 cm×20 cm,活性区高度为160 cm,径向和轴向含有厚度为20 cm的水反射层,且堆芯内的控制棒在瞬态过程以相同的速度分别提出和插入堆芯。
采用控制棒部分插入显式表示法及体积权重法,对LMW三维瞬态基准问题进行数值计算,计算结果示于图3。
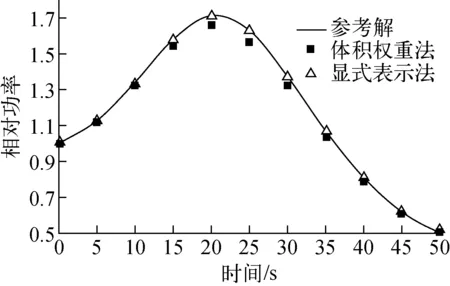
图3 LMW基准问题数值结果
从图3可看出,采用一般的体积权重法进行计算会引入较大偏差(即锯齿效应),功率的最大相对偏差可达4%左右,且在瞬态功率峰值附近。采用显式表示法后,这种偏差基本上完全消除,因而本方法在动力学计算中取得了非常好的效果。需要说明的是,文献[5]通过更复杂的模型取得了类似的结果。
3 结论和建议
针对锯齿效应,本文提出了一种在节块法中对部分插入控制棒节块的显式表示方法,即在对节块法横向积分方程的推导中显式考虑轴向含部分插入控制棒节块的非控制棒区截面和控制棒区截面(即中子截面阶跃函数)。通过稳态控制棒微分价值计算和瞬态动力学数值计算,表明本文提出的方法大幅缓解了锯齿效应,特别是在瞬态动力学问题中基本上完全消除了该效应带来的偏差,取得了很好的效果。
此外,本文提出的显式表示方法不仅可用于考虑部分插入控制棒这种节块内截面不均匀的问题,同样也可考虑如燃料组件格架(甚至多个格架)引起的节块内截面不均匀问题,这有待进一步进行研究。
感谢赵荣安教授在本文研究中给予的帮助和有益讨论。
参考文献:
[1]CHO N. Fundamentals and recent developments of reactor physics methods[J]. Nuclear Engineering and Technology, 2005, 37(1): 25-78.
[2]ZIMIN V G, NINOKATA H, POGOSBEKYAN L R. Polynomial and semi-analytic nodal methods for nonlinear iteration procedure[C]∥PHYSOR-98. Long Island: [s. n.], 1998: 994-1 002.
[3]SMITH K S. An analytic nodal method for solving the two-group, multidimensional, static and transient neutron diffusion equations[D]. USA: Massachusetts Institute of Technology, 1979.
[4]CHAO Y A, HUANG P. Theory and performance of the fast-running multidimensional pressurized water reactor kinetics code, SPNOVA-K[J]. Nucl Sci Eng, 1989, 103: 415-419.
[5]de LIMA Z R, MARTINEZ A S, da SILVA F C, et al. Correcting the cusping problem in three-dimensional transients through NEM modification[J]. Nucl Sci Eng, 2012, 170: 66-74.

