屏蔽式核主泵动静转子间的压力脉动特性
朱 跃,张继革,尹俊连,程 辉,王德忠
(上海交通大学 机械与动力工程学院,上海 200240)
反应堆冷却剂循环泵(简称核主泵),其主要用途是给反应堆供给冷却剂,实现冷却剂在一回路系统内循环,以保证将反应堆的热量带走。其长时间稳定安全的运行对冷却堆芯、防止核电站事故的发生及恶化极为重要,因此,核主泵常被喻为核电站的“心脏”。核主泵由于其空间结构的不对称性、高速旋转的叶轮与静止的导叶和蜗壳之间的动静干涉相互作用、正常运行过程中核主泵内部复杂的三维非定常湍流等,会引起主泵内的压力波动,这不仅会对核主泵的扬程、流量和效率等外特性产生影响,而且会引起机组设备的振动和噪声。因此,研究核主泵内部的压力脉动对降低机组的振动、提高泵长期运行稳定性具有重要意义。
国内外学者对泵的压力脉动进行了相关研究。徐朝晖等[1]采用三维RNG湍流模型及滑移网格技术建立动静交界面,对高速离心泵中的动静干扰引起的非定常流场进行了计算,并分析了流体诱发的压力脉动特性。刘阳等[2]对离心泵压力脉动进行了分类,得出压力脉动主要包括轴频倍频压力脉动、叶频倍频压力脉动和随机压力脉动。Fortes-Patleea等[3]应用重叠网格和相位滞后的周期边界条件,对蜗壳泵内叶轮和蜗壳的动静干扰进行了二维非定常计算。尹俊连等[4]采用分离涡模拟(DES)方法对小流量下水泵水轮机导叶处的压力脉动进行了预测,发现固定导叶内部的压力脉动未受到叶轮的影响。因此,本文对某缩尺比为1∶4的屏蔽式核主泵模型泵内部压力脉动进行研究。
1 数值计算模型及方法
1.1 泵的基本参数
本研究的计算模型为某屏蔽式核主泵模型泵,模型泵缩尺比为1∶4,其参数列于表1。

表1 模型泵主要参数
1.2 计算区域和计算网格
模型泵全流道共有4个组成部分:叶轮、导叶、进口和出口。将模型泵4个部分几何模型导入网格划分软件ICEM进行网格划分。由于六面体网格较四面体网格更易收敛;同样网格尺寸,数量更少,计算时间更短等优点,因此对模型泵进行全流道六面体网格划分。图1为模型泵的网格模型。其中,叶轮的网格数为601 757,导叶的网格数为578 325,进口的网格数为224 585,蜗壳及出口的网格数为584 029,总的网格数为1 988 699。并对边界层网格进行了加密。
1.3 计算方法
本研究选用商业软件CFX运用有限体积法进行求解。进口边界条件设置为质量流量,出口边界条件设置为平均静压,壁面选用无滑移壁面。
为预估模型泵的扬程、轴功率和效率与流量的关系,首先对其进行定转速稳态计算。模型泵性能计算的工况点选择为额定流量的20%、40%、60%、80%、100%、120%,计算曲线均布于整条曲线上。定转速稳态计算的实现采用旋转参考坐标系(MRF),该方法将旋转部分定义为1个域,该域内增加由于旋转引起的非惯性力,包括离心力和科氏力,而外部可以是静态的。
为求解模型泵的压力脉动,需对其进行定转速瞬态计算。定转速瞬态计算的基本思想是旋转态滑移面的思想[5],通过滑移网格模型模拟动静转子之间的流场,即在叶轮进口前和叶轮出口后形成两套滑移网格,转轮部件的网格相对于导叶和进口的网格转动,交界面两侧的网格节点不相互重合[6]。将定转速稳态计算结果作为瞬态计算的初场,转速设定为额定转速1 780 r/min。为精确模拟模型泵的瞬态流场,时间步长选择叶轮旋转2°所需的时间,即0.000 186 s,叶轮旋转总的计算时间为叶轮旋转15圈所需的时间,即0.500 5 s。如图2所示,在模型泵动静转子1周每隔30°角度设置1个检测点,1周共24个监测点。分别计算额定流量的60%、80%、100%、120%和140%等5种典型工况下的压力脉动特征。

图1 模型泵全流道六面体网格(a)、叶轮六面体网格(b)及导叶六面体网格(c)
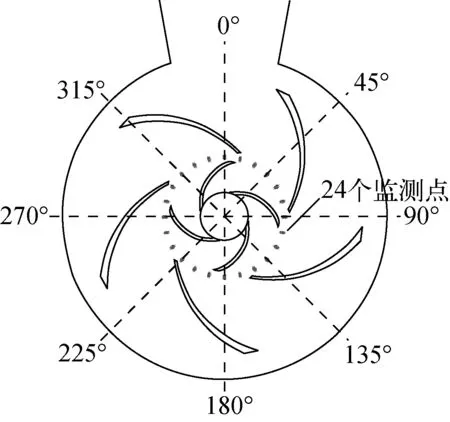
图2 模型泵动静转子间监测点布置
1.4 湍流模型的选取
在定转速稳态计算的湍流模型选取上,主要有标准k-ε模型、RNGk-ε模型、k-ω模型和SST模型。相关文献[7]研究表明,上述模型对泵稳态性能模拟结果的相对误差在1%以内。为了兼顾计算资源和收敛难度,本研究选用标准k-ε模型作为稳态计算使用的湍流模型。
在定转速瞬态计算的湍流模型选取上,理论界已发展了雷诺平均N-S方程(RANS)、大涡模拟(LES)以及结合两种模式的分离涡模拟(DES)。RANS模型由于其对计算资源要求相对较低、收敛难度低等优点,在流体机械的工程计算中得到了大量应用[8]。计算时间表明,RANS模型可满足求解无叶区压力脉动的需要,但捕捉的压力脉动的频率有限[9]。这是由于RANS模型在多尺度流动模拟中还不是很成熟。而DES模型在各种复杂工况下均有较好的表现。DES模型在近壁面采用LES模型进行模拟,其他区域采用RANS模型。采用DES模型计算模型泵瞬态流动在计算精度和计算资源之间得到了较好的平衡。张宇宁等[10]在尾水管的涡带演化及压力脉动预测中,发现DES模型得到的流态及压力脉动的幅频特性优于RNGk-ε模型。因此,定转速瞬态计算选择DES模型。
2 数值模拟结果及分析
2.1 网格无关性分析
为验证网格数量无关性,分别选取不同网格数量进行计算,计算的工况为额定工况,运行流量为280 m3/h。选择模型泵的扬程和轴功率作为网格无关性计算的目标参数,观察其随不同网格数量的变化情况(图3)。从图3可看出,扬程和轴功率随网格数量的增大而减小。当网格数量达200万后,扬程和轴功率基本保持不变,此时可认为与网格数量无关。因此,选取200万的网格数量作为数值模拟计算的网格数量,以保证计算结果的可靠性和最大程度降低计算资源。
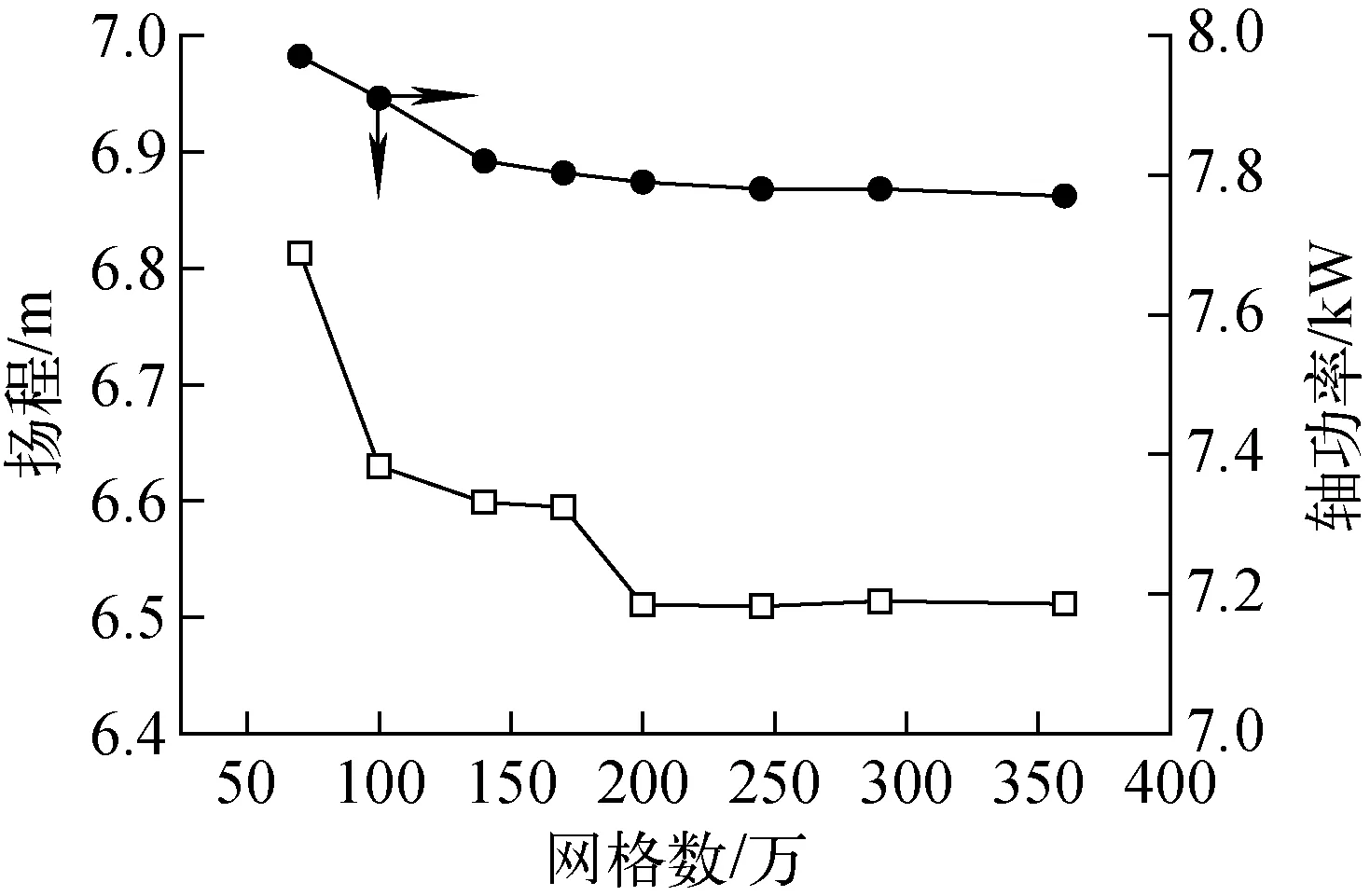
图3 扬程和轴功率的网格无关性分析
2.2 模型泵外特性验证
为验证数值模拟的准确性,对模型泵外特性参数进行了实验验证。图4示出实验得到的扬程-流量、效率-流量曲线与数值模拟结果的对比。从图4可看出,实验结果与数值模拟结果在趋势上一致,且在靠近额定工况点,两者的结果基本相等。在小于额定工况点时,扬程和效率的数值模拟结果略小于实验结果,这是因为湍流模型对小流量下泵内部复杂流场表现不够精确,但数值模拟结果和实验结果的偏差在可接受范围内;而在额定工况点及其附近结果吻合较好,数值模拟得到的扬程和效率较实验结果偏大,这是因为数值模拟中未考虑泵的容积泄漏、摩擦损失等因素。可见,数值模拟较为准确地预测了模型泵的外特性,也为进一步预测压力脉动提供了保证。
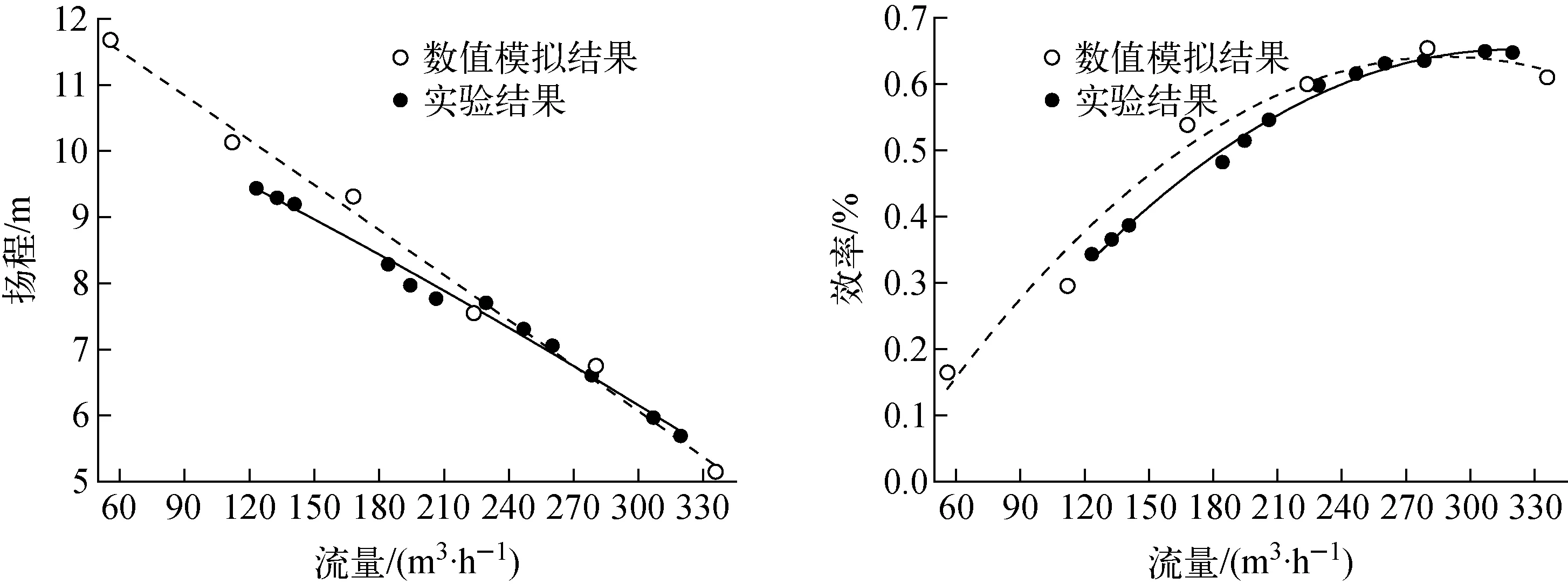
图4 扬程和效率的实验结果与数值模拟结果对比
2.3 动静转子之间压力脉动分析
1) 动静转子不同部位的压力脉动特性
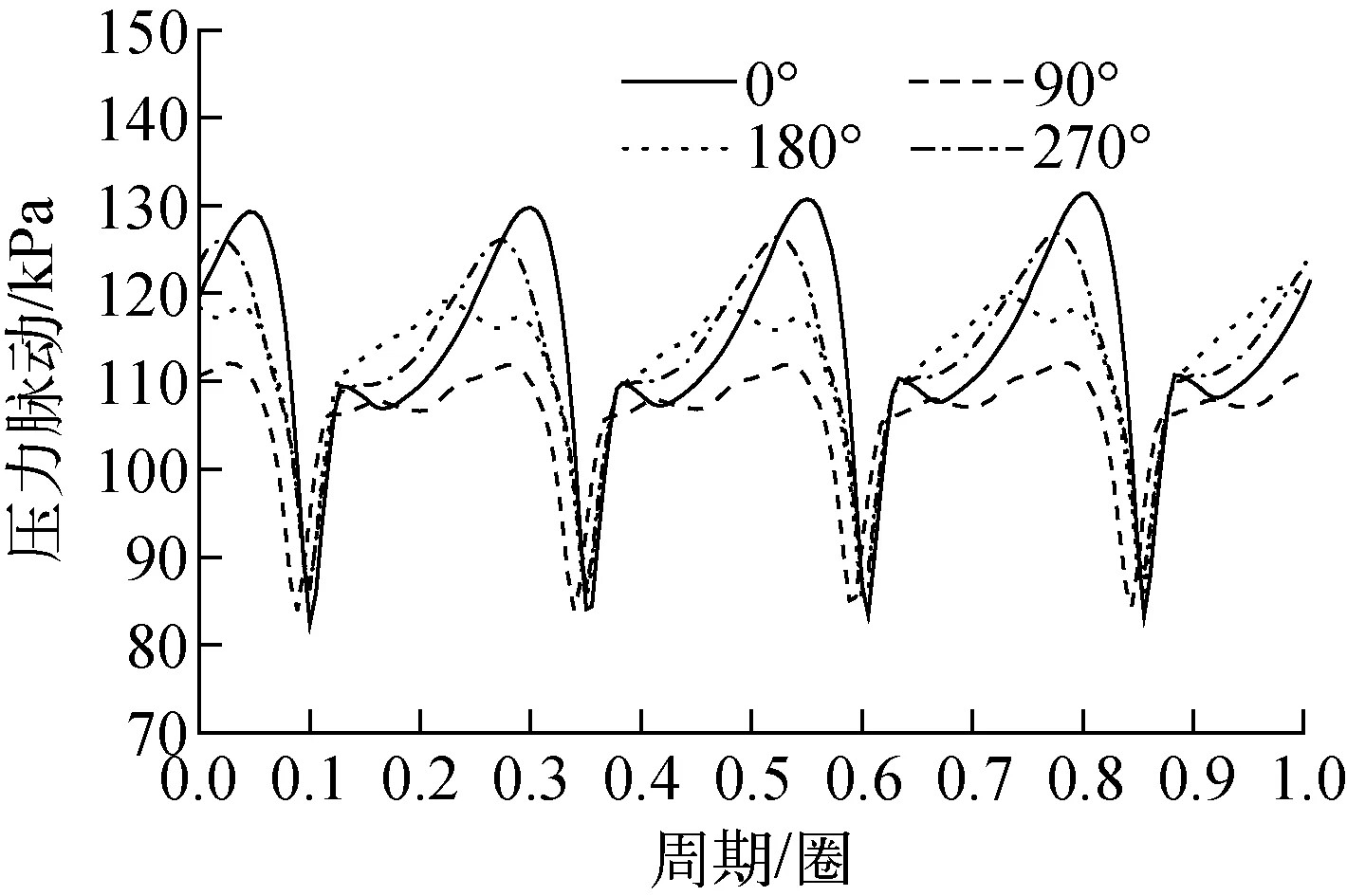
图5 动静转子间压力脉动时域图
采用DES模型对模型泵进行了非定常湍流数值模拟,得到了模型泵动静转子之间24个监测点处的压力脉动。为了确定不同位置处压力脉动的特征,分别选取额定工况下0°、90°、180°和270°等4个典型位置处的压力脉动进行时域分析,结果如图5所示。从图5可明显看出,在1个周期内4个工况点均出现了4个小周期。4个工况点的压力脉动波谷基本一致,约为82 kPa;而4个工况点的波峰不同,0°位置处的压力脉动波峰最大,约为130 kPa,270°位置处的压力脉动波峰其次,约为126 kPa,180°位置处的压力脉动波峰约为120 kPa,90°位置处的压力脉动波峰最小,约为112 kPa。因此,动静转子之间的压力脉动在靠近出水管处的压力脉动最大。从出口向逆时针旋转压力脉动波动幅度逐渐递减。图6为动静转子之间的压力脉动波动幅度随位置的分布,圆周方向为动静转子之间压力脉动监测点的位置,径向为动静转子之间压力脉动波动幅值,即压力脉动波峰与压力脉动波谷之差。从图6可看出,从0°开始逆时针旋转依次出现5个压力脉动波动幅度的波峰,分别在345°、255°、180°、120°和60°处,且波峰峰值随逆时针方向逐渐递减,在导叶入口边处压力脉动的波动幅度出现极小值。

图6 动静转子间压力脉动波动幅度
为了解模型泵动静转子之间的压力脉动特性及振源,对其时域图进行FFT变换得到压力脉动频率图。图7为动静转子间压力脉动频域图,可看出,0°、90°、180°和270°等4个典型位置处压力脉动的振动频率是轴频的4n倍,这是因为模型泵的叶轮叶片数目为4,而动静转子之间的压力脉动主要是由动静转子之间的相互干涉引起的,所以其压力脉动的频率为叶轮叶片转过的频率及其倍频。这是由于从叶轮出口边到导叶内部产生了大的速度梯度,且在导叶压力面上低速度流场的形成导致流体离开叶轮时形成射流尾迹,射流尾迹的宽度与到叶轮出口点射流源的距离呈正比,射流尾迹中心线上的最大速度与到射流源的距离的平方呈反比,因此随此距离的增大,射流尾迹的最大速度越来越小。图8为监测点截面速度场,其中靠近出口管道处的导叶压力面存在一较大的低速度流体域且从叶轮出口到导叶存在一很明显的速度梯度。图9为监测点截面涡量场,其中在导叶尾部的细长带状区域即为射流尾迹。当叶轮尾部的射流尾迹接近导叶进口边时,射流尾迹将被导叶切割成几个部分,从而尾迹从叶轮出口边脱落和主流一起流入导叶,然后继续在导叶内部被剪切、拉伸和演化。这种现象伴随叶轮旋转而周期性的发生,引起动静转子之间的压力和速度周期性的波动,从而形成动静转子之间的压力脉动。从时间t=0.006 975 s至t=0.013 671 s为叶轮射流尾迹从形成、与导叶进口边接触、被导叶进口边切割和叶轮射流尾迹脱离叶轮继续在导叶内部被剪切、拉伸和演化的全过程。在此过程中,导叶的边界层也因叶轮转动而发生周期性的不稳定变化。

图7 动静转子间压力脉动频域图
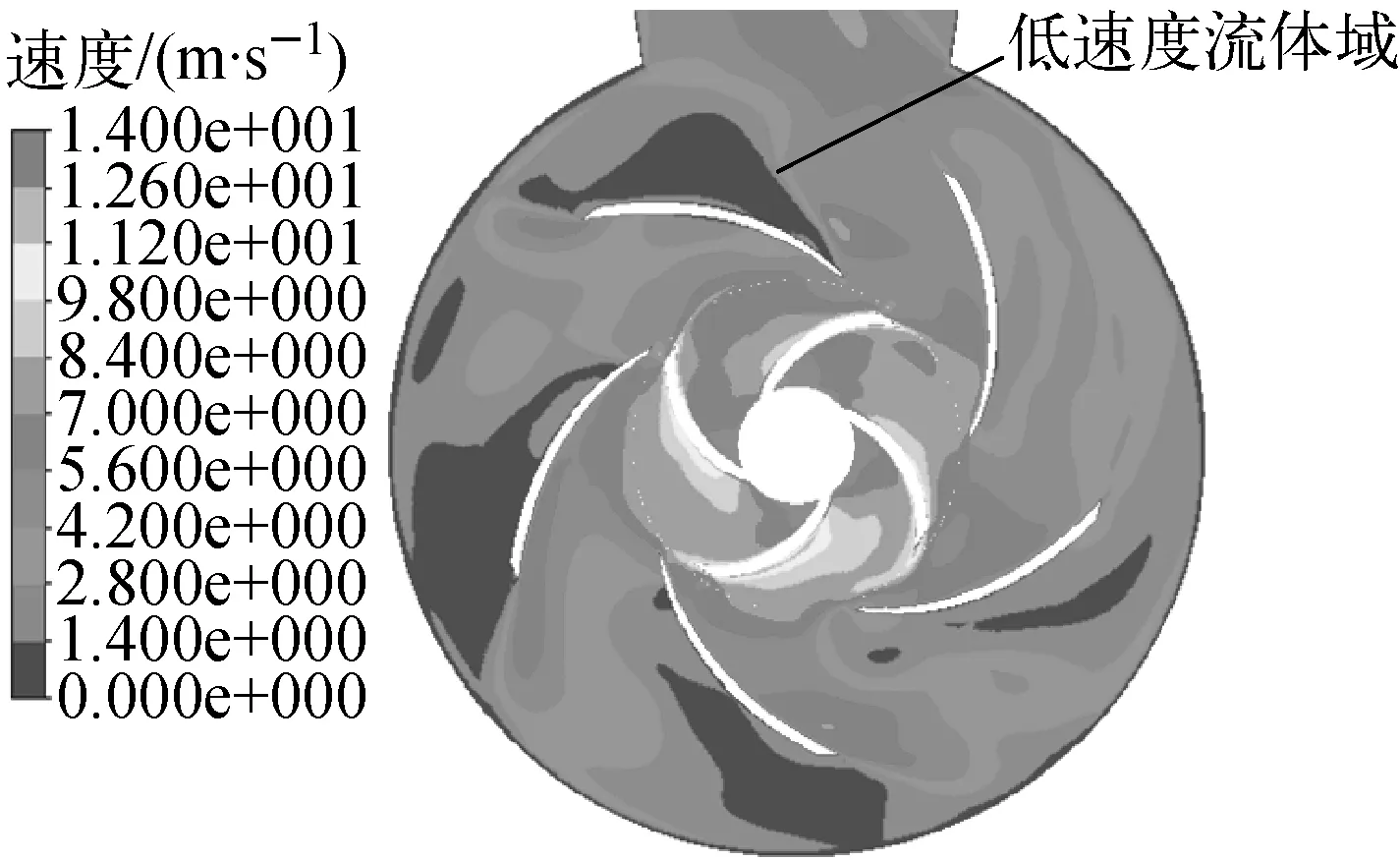
图8 模型泵监测点截面速度场
2) 不同工况下动静转子间压力脉动特性
图10示出不同流量工况下0°位置处监测点在1个周期内的压力脉动时域图。从图10可见,压力脉动的绝对振动幅度随流量的增加而增大,在140%额定流量下最大,在60%额定流量下最小,这是由于射流尾迹的强度和泵运行流量的大小呈正相关,而且这也是由于核主泵特殊的类圆形蜗壳决定的。将0°监测点在不同工况下的压力脉动时域图进行FFT变换后得到其在不同工况下压力脉动频域图,如图11所示。从图11可看出,不同流量工况下压力脉动频率的主频均为叶频及其倍频,这与前文的分析一致。
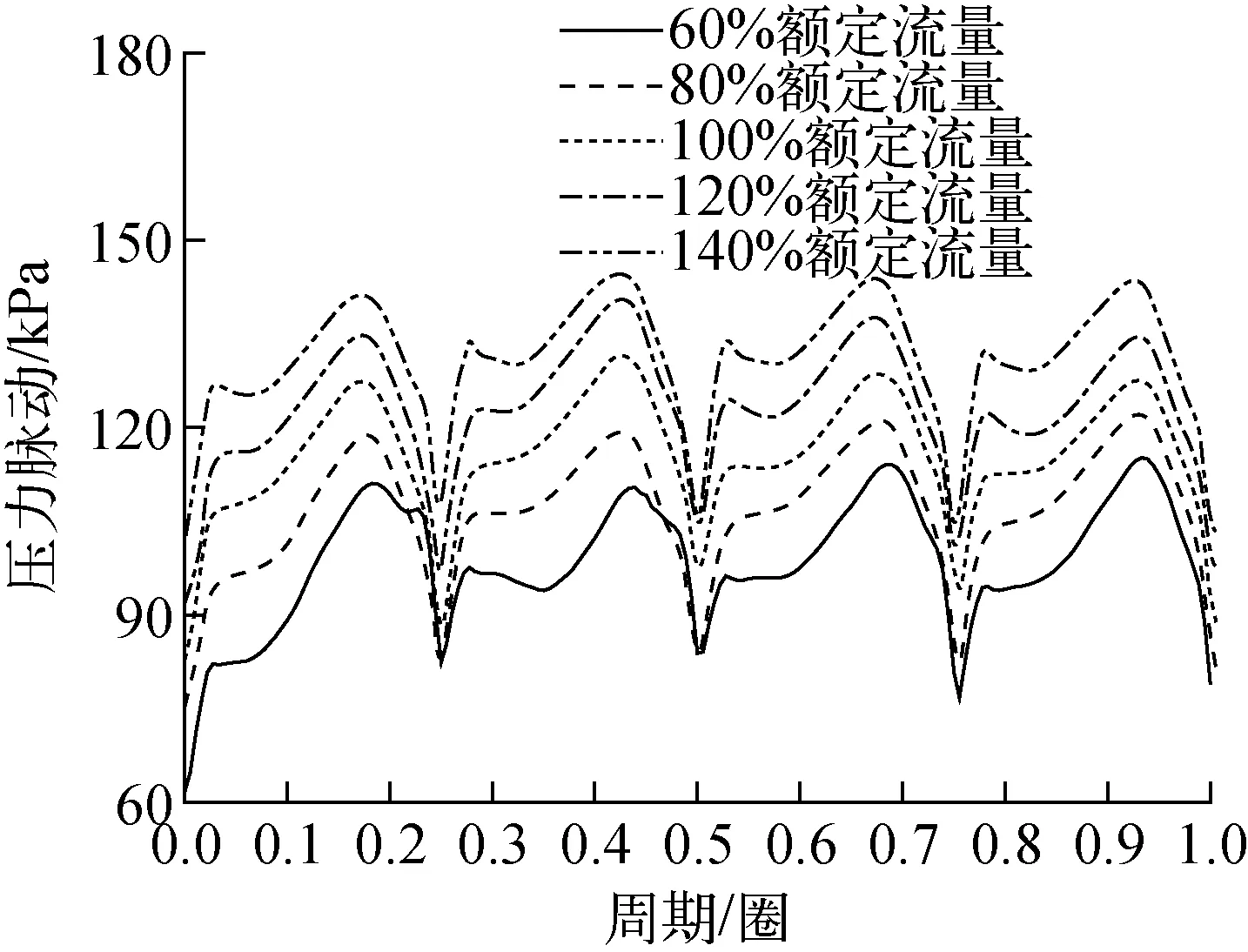
图10 0°监测点不同工况下压力脉动时域图
3) 动静转子间压力脉动的传播
图12为0°~345°范围内24个监测点的压力脉动时域图。从图12a可见,压力脉动波峰的传播无明显规律性,但压力脉动波谷的传播有着明显的周期性,在1个周期内每个监测点出现4次波谷,在0.1~0.35 s时间段内,可看到75°、60°、45°、30°、15°和0°监测点依次出现了压力脉动的波谷。因为波谷处压力较低,从而形成低压区,对照图6所标的刻度可发现该低压区在0.1~0.35 s时间段内沿逆时针方向从75°监测点传播到0°监测点。且此低压区的传播速度和叶轮转速相同。观察图12b、c、d可发现同样的现象,在0.1~0.35 s时间段内分别有3个低压区,在90°~165°、180°~255°和270°~345° 3个区域内沿逆时针方向运行。所以模型泵在动静转子之间同时存在4个低压流体区域,且每个低压区域以叶轮转动速度传播。
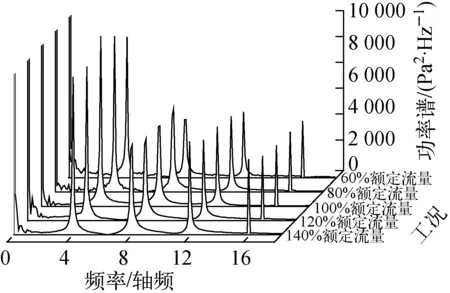
图11 0°监测点不同工况下压力脉动频域图
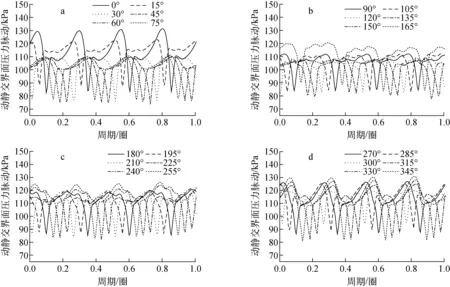
图12 各监测点压力脉动时域图
3 结论
本文采用分离涡模拟方法对核主泵模型泵内动静转子之间的压力脉动进行了分析,取得的主要结论如下:
1) 核主泵模型泵动静转子之间压力脉动的频率为叶频及其倍频,这是由于叶轮出口边的射流尾迹和导叶入口边的相互切割作用,引起动静转子之间的压力和速度周期性的波动,从而形成动静转子之间的压力脉动。
2) 核主泵模型泵动静转子之间压力脉动的振动幅度在蜗壳出口处最大,并沿逆时针方向逐渐减小。到导叶入口位置压力脉动的振动幅度出现极小值。这说明导叶入口在不同位置处所受到的动应力是不同的。核主泵模型泵动静转子之间压力脉动的振动幅度随运行流量的增大而变大。所以应注意核主泵在启动、停机和惰转等瞬态工况下的运行,保证其在瞬态运行工况下的安全性。
3) 核主泵模型泵的低压区数量和叶轮叶片数相同,低压区的传播速度为叶轮的转速。这说明叶轮出口边和导叶的进口边存在一周期性的疲劳载荷,所以在核主泵设计中应预估叶轮和导叶的疲劳寿命,保证核主泵的长时间使役。
综上所述,核主泵动静转子之间的压力脉动对核主泵安全运行有着重要影响,在核主泵的设计和运行过程中应对其充分考虑。
参考文献:
[1]徐朝晖,吴玉林,陈乃祥,等. 高速泵内三维非定常动静干扰流动计算[J]. 机械工程学报,2004,40(3):1-4.
XU Chaohui, WU Yulin, CHEN Naixiang, et al. Unsteady blade-row interaction calculation in high speed pump[J]. Chinese Journal of Mechanical Engineering, 2004, 40(3): 1-4(in Chinese).
[2]刘阳,袁寿其,袁建平,等. 离心泵的压力脉动研究进展[J]. 流体机械,2008,36(9):33-37.
LIU Yang, YUAN Shouqi, YUAN Jianping, et al. Overview of pressure fluctuation in centrifugal pump[J]. Fluid Machinery, 2008, 36(9): 33-37(in Chinese).
[3]FORTES-PATLEEA R, LONGATTE F, KUENY J L, et al. Numerical analysis of unsteady flow in a centrifugal pump[J]. ASME Fluid Machinery, 1995, 222: 41-46.
[4]尹俊连,刘锦涛,王乐勤,等. 水泵水轮机泵工况小流量区压力脉动预测[J]. 工程热物理学报,2011,32(7):1 141-1 144.
YIN Junlian, LIU Jintao, WANG Leqin, et al. Prediction of pressure fluctuations of pump turbine under off-design condition in pump mode[J]. Journal of Engineering Thermophysics, 2011, 32(7): 1 141-1 144(in Chinese).
[5]LI Zhifeng, WU Dazhuan, WANG Leqin, et al. Numerical simulation of the transient flow in a centrifugal pump during startup period[J]. ASME Journal of Fluids Engineering, 2010, 132: 081102.
[6]刘树红,邵奇,杨建明,等. 三峡水轮机的非定常湍流计算及整机压力脉动分析[J]. 水力发电学报,2004,23(5):97-101.
LIU Shuhong, SHAO Qi, YANG Jianming, et al. Unsteady turbulent simulation of Three Gorges hydraulic turbine and analysis of pressure in the whole passage[J]. Journal of Hydroelectric Engineering, 2004, 23(5): 97-101(in Chinese).
[7]BARRIO R, FERNANDEZ J, BLANCO E, et al. Estimation of radial load in centrifugal pumps using computational fluid dynamics[J]. European Journal of Mechanics B, 2011, 30: 316-324.
[8]王福军. CFD在水力机械湍流分析与性能预测中的应用[J]. 中国农业大学学报,2005,10(4):75-80.
WANG Fujun. Application of CFD to turbulent flow analysis and performance prediction in hydraulic machinery[J]. Journal of China Agricultural University, 2005, 10(4): 75-80(in Chinese).
[9]张宇宁,刘树红,吴玉林,等. 混流式水轮机压力脉动精细模拟和分析[J]. 水力发电学报,2009,28(1):183-186.
ZHANG Yuning, LIU Shuhong, WU Yulin, et al. Detailed simulation and analysis of pressure fluctuation in Francis turbine[J]. Journal of Hydroelectric Engineering, 2009, 28(1): 183-186(in Chinese).
[10] 张宇宁,刘树红,吴玉林,等. 应用新型导叶的混流式水轮机DES模拟[J]. 工程热物理学报,2007,28(1):139-141.
ZHANG Yuning, LIU Shuhong, WU Yulin, et al. DES simulation on Francis turbine with new guide vanes[J]. Journal of Engineering Thermophysics, 2007, 28(1): 139-141(in Chinese).

