破碎射气介质内氡渗流运移和析出规律的实验研究
王立恒,叶勇军,,*,丁德馨,赵娅利,范楠彬,钟永明
(1.南华大学环境保护与安全工程学院,湖南衡阳 421001;2.南华大学铀矿冶生物技术国防重点学科实验室,湖南衡阳 421001)
长期吸入高浓度的氡及其子体容易诱发肺癌[1-6],因此氡污染问题备受各国学者关注。土壤、建筑材料以及铀矿开采过程中的爆破铀矿石堆、地表堆浸场、废石堆、尾矿堆等含铀镭射气介质是大气氡的主要来源。这些介质中的226Ra衰变产生氡,当氡原子离开介质的固体晶格进入微裂隙和裂隙形成可迁移的氡,随后在浓度梯度和压力梯度的作用下沿着颗粒间连通的孔隙通道运移[7]。因此,氡在射气介质中主要以扩散和渗流两种方式运移。
目前,国内外学者根据扩散和渗流理论在获取射气介质内氡的运移和析出规律方面开展了大量的理论和实验研究。Rogers等[8]提出了基于氡扩散与对流机制的迁移理论模型,得到了土壤中氡活度浓度分布的表达式。何斌等[9]在前人理论模型的基础上,通过对土壤和岩石中氡活度浓度及其表面析出率的边界条件的探讨,给出了土壤和岩石中氡活度浓度及其表面氡析出率的具体表达式。孙凯男[10]总结了前人计算土壤氡析出率的理论和经验公式,建立了土壤中氡扩散析出率的简化理论模型,并用实测数据对该模型进行检验,结果表明该模型能预测土壤氡析出率。Yakovleva等[11]建立了氡在多层多孔介质中运移的稳态方程组,并用有限差分法对其求解,获得了氡在不均匀多孔介质中的浓度分布规律。申超等[12]对6种均匀土壤及典型层状土壤中氡活度浓度的分布进行数值模拟,得出了不同土壤中氡活度浓度与土壤深度的关系。曹众为等[13]通过模型实验对不同压力梯度下多孔介质两侧的氡析出率进行研究,发现一定压力梯度范围内多孔介质两侧的总氡析出率随压力梯度增大而增大。
综上所述,国内外对氡在射气介质中运移和析出规律的研究大多局限于岩石、砂石和土壤等细粒级(或孔道较小)的介质,而对广泛存在于铀矿山的井下爆破铀矿堆和井上堆浸场等含有颗粒平均粒径较大,且具有较高的渗透性、孔隙度和铀镭含量的有限厚破碎射气介质的研究较少。在这些破碎射气介质内,高浓度的氡气很容易在压力梯度的作用下沿着孔隙运移,进而造成井下和井上大气氡的污染。因此,研究渗流状态下氡在这类破碎射气介质中的运移和析出,对于铀矿山的氡防护有着重要的意义;同时,也可为氡气在各种地质环境下的运移提供理论参考。为此,本文通过室内实验和理论相结合的方法,研究不同渗流速度下有限厚破碎射气介质内氡运移以及介质表面氡析出率的变化规律。
1 实验
1.1 实验原理
破碎射气介质内氡活度浓度变化的因素有:介质中226Ra衰变产生的氡、氡气的扩散运移、氡气的渗流迁移、氡气自身的衰变。据此,可建立孔隙介质中氡稳态运移的一维微分方程[14]。式中:c(x)为介质内x位置处的孔隙氡活度浓度,Bq·m-3;D为氡在介质中的扩散系数,m2·s-1;λ为氡的衰变常数,λ=2.1×10-6s-1;α为介质内可运移氡的产生率,Bq·m-3·s-1;v为介质内气体的渗流速度,m·s-1;η为介质的孔隙度;x为介质距渗流入口的距离,m。
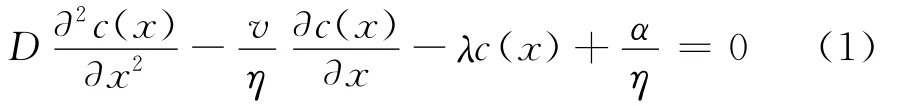
当破碎射气介质内氡的运移完全由渗流所主导时,可忽略氡的扩散运移作用[14],式(1)可简化为:
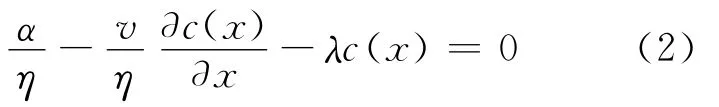
对于边界条件x=0,c(0)=0Bq·m-3时,式(2)的解析解即为一维破碎射气介质中氡活度浓度分布函数:

从式(3)可知,破碎射气介质中的氡活度浓度分布与表面氡的析出率不仅与介质本身的物理特征(位置和可运移氡的产生率)有关,而且也受介质内空气渗流速度的影响。
1.2 实验材料与装置
实验用矿石来自我国南方中低温热液充填交代花岗岩单铀矿床,矿石中的矿物由热液矿物和围岩残留矿物组成。矿山提供的矿物分析资料表明矿石的脉石矿物为石英、微斜长石、萤石、绿泥石和方解石,铀矿物以条状形式被其他矿物包裹,而整个铀矿又被石英矿物包裹,主要铀矿物为沥青铀矿及少量铀的次生矿物,并与黄铁矿、石英等共生。本实验用矿石样品粒径为4~5mm,矿石密度为2.61×103kg/m3,铀品位约为0.145%,铀镭平衡系数约为1.04。实验柱内装入矿石高度2.5m,质量28.25kg,由于该岩石的硬度系数f=8~10,岩性致密且稳定,采用分层装矿石样,且实验柱内样品的高度较小,实验中可忽略矿石自重对实验柱内样品孔隙度和密度的影响,通过测试得到整个试样的平均孔隙率为44.88%。
所用实验装置主要由供气系统和实验筒体组成,如图1所示。供气系统用以检查装置的气密性并提供实验所需的稳定风流,主要包括气泵、流量计、恒温装置和阀门等,各部分通过外径10mm的PU管串接在管路中,连接端口用强力胶密封;实验时恒温装置控制气流温度为10℃。实验筒体是实验装置的主要部分,总高约为2.76m,主要由底座(高0.2m)、5个单元装矿筒体(外径为0.11m,内径为0.1m,高度为0.5m)和顶盖(高0.04m)通过密封垫圈、法兰和连接螺栓串联而成。为防止装样和渗流实验过程中细颗粒的流失,在底座与最下层装矿筒体连接处夹10mm厚的塑料孔板,孔板的孔隙率为45%;并在孔板上铺孔径为0.5mm的滤网。为确定渗流过程中的压力梯度,在实验筒体同一侧间隔2m处开2个直径为6mm的安装孔,两孔均安装一根外径为6mm的测压管,测压管通过橡皮管与U型压力计相连。为获得不同高度处的孔隙氡活度浓度,在整个有机玻璃管柱高度为0.45、0.95、1.45、1.95、2.45m的筒壁上开直径为8mm安装孔,各孔均安装一根内直径6mm的多孔小管,小管一端用纱布包裹并深埋入松散射气介质中,另一端用橡胶塞密封。

图1 一维渗流实验装置
1.3 实验过程
1)装样
依次将隔板和装矿筒体2置于底座上,并用法兰将其固定。取配好的试样,称重后分层装入装矿筒体2内,用木锤轻轻捣实,当试样与装矿筒体2平齐时,用法兰将装矿筒体2与装矿筒体1相连。采用相同的方法装样,并连接上一层实验筒,直至将5个装矿筒体全部连接好,最后通过法兰将顶盖与最上层实验筒相连。
2)装置密封性能检查
启动气泵,打开阀门1和流量计,使空气缓慢进入实验装置,待U型压力计的读数达到一定值后,关闭气泵和阀门1,观察U型压力计的读数是否稳定。如不稳定,检查装置的气密性,调整好后再进行实验。
3)不同渗流速度下压力梯度的测量
启动气泵,打开阀门1、2、3和流量计,待流量计和U型压力计的读数稳定后,记录流量计的流量以及U型压力管内液面的高度差。调节流量计,变更流量,重复测量工作。
4)稳定渗流下孔隙氡活度浓度的测量
更换气泵和流量计,调节流量计使其固定在某一读数,以确保空气在射气介质中发生稳定渗流。由于气流渗流速度较大,造成装置的氡活度浓度较低,此时若取样太小会导致测得的单个计数率代表的实际氡活度浓度较大,增大了测量结果的误差;若取样太大试样很容易受其他位置处氡的干扰。为获得准确的氡活度浓度,通过比较不同取样体积的测量结果,选用50mL为取样体积。当介质内氡活度浓度稳定之后,自上而下,采用50mL针孔注射器缓慢抽取试样高度为0.45、0.95、1.45、1.95、2.45、2.50m处取样管内的氡气,将其注入0.5L球形闪烁室中封存。3~3.5h后,将闪烁室置于FD-125型氡钍分析仪的工作平台上并对准光电倍增管,记录FH463B型智能定标器的计数率(min-1)[15]。变更流量,重复测试工作。
2 实验数据的处理
破碎介质内空气的渗流速度按下式计算:
v=Q/A
(4)
式中:Q为空气流量,m3/s;A为矿样横截面积,A=0.007 9m2。
压力梯度按下式计算:
Δp=ρgΔh/L
(5)
式中:Δp为压力梯度,Pa·m-1;ρ为水的密度,ρ=1×103kg·m-3;g为重力加速度,g=9.8m·s-2;Δh为U型压力管两侧水的高度差,m;L为两测点间的距离,对于本装置L=2m。
孔隙氡活度浓度按下式计算:

式中:c为孔隙氡活度浓度,Bq·m-3;NC为本底加样品计数率的平均值,min-1;NB为本底计数率的平均值,min-1;NK为室内空气氡活度浓度所对应的计数率,min-1;VS为闪烁室体积,对于本实验VS=500mL;V为针孔注射器取样体积,对于本实验V=50mL;K为刻度系数,Bq/(m3·min)。
在本文所给稳定渗流的实验条件下,介质表面空气中氡的活度浓度是稳定的,氡析出率按下式计算:
J=vC′A
(7)
式中:J为矿样表面的氡析出率,Bq·m-2·s-1;C′为矿样表面顶盖内氡的活度浓度,Bq/m3。
根据式(4)和式(5)可得不同渗流速度下介质内的压力梯度,相关结果列于表1,不同渗流速度下矿柱内6个不同高度处的孔隙氡活度浓度以及介质表面氡析出率列于表2。

表1 不同渗流速度下试样内的压力梯度
3 破碎射气介质氡运移和析出规律
3.1 空气在破碎射气介质内渗透率的确定
压力梯度随渗流速度变化的散点图如图2所示。
从图2可见,压力梯度与气体渗流速度之间呈线性关系,这说明,试样中的渗流满足Darcy公式,为此,可采用Darcy公式描述压力梯度与渗流速度之间的关系:

式中:k为空气在介质中的渗透率,m2;μ为空气的动力黏度系数,对于本实验,μ=1.78×10-5Pa·s。

表2 不同渗流速度下各高度处的孔隙氡活度浓度以及介质表面的氡析出率

图2 压力梯度随渗流速度变化的散点图
将渗流速度与压力梯度按式(8)进行拟合,可得空气在实验柱内的渗透率为1.400×10-8m2。不同渗流速度下可运移氡产生率的估算结果列于表3。结合表1和表3可知,较小的压力梯度能使空气在破碎射气介质内产生较大的渗流速度,因此,破碎射气介质内氡的运移很容易由渗流主导。

表3 不同渗流速度下可运移氡产生率的估算结果
3.2 氡渗流主导作用下破碎射气介质内可运移氡产生率的估算
根据表2中孔隙氡活度浓度的测量数据,用非线性最小二乘法按式(3)进行拟合,得到的不同渗流速度下以及不同高度处可运移氡产生率的拟合结果分别列于表3、4。

表4 不同高度矿柱可运移氡产生率的估算结果
由表3和表4可见:1)拟合结果具有很好的相关性,其相关系数达0.99以上,这说明当渗流速度或压力梯度超过一定值时,试样中的氡主要以渗流方式迁移,此时可用式(3)来研究氡在破碎射气介质中的运移规律;2)除表4中高度0.45m处可运移氡产生率的估算值与平均值的相对偏差高达9.46%外,其他可运移氡产生率的估算值与平均值的相对偏差均在4.5%以下,0.45m处相对偏差高的原因可能是测得的孔隙氡活度浓度偏低,这可能是由于破碎射气介质产生的一部分氡由下表面析出,或隔板孔隙结构不均匀及与射气介质孔隙结构的差异,造成射气介质靠孔板区域的氡活度浓度的分布不均匀,导致取样浓度偏小。以上结果表明,可通过测量破碎射气介质同一位置处不同渗流速度下的孔隙氡活度浓度或同一渗流速度不同位置处的孔隙氡活度浓度,再联合式(3)和非线性最小二乘法获取射气介质的可运移氡产生率。
3.3 破碎射气介质内氡活度浓度分布规律
不同渗流速度下孔隙氡活度浓度随介质高度变化如图3所示,图中的散点为实测值,曲线为估算参数所对应的理论计算值。
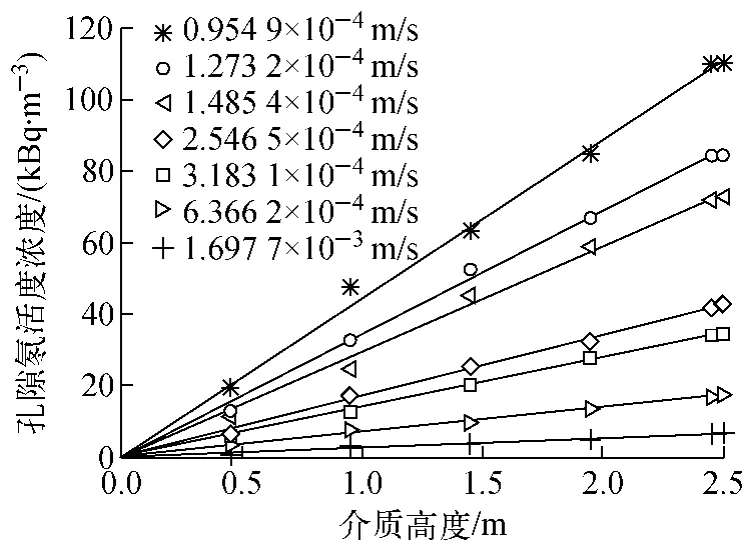
图3 不同渗流速度下孔隙氡活度浓度随介质高度的变化
由图3可见,在本文所给矿样高度下,当渗流速度处于0.954 9×10-4~1.697 7×10-3m/s时,同一渗流速度下孔隙氡活度浓度随着介质高度近似呈线性增长。
实验柱内不同高度处矿样内的孔隙氡活度浓度随渗流速度的变化如图4所示,图中的散点为实测值,曲线为表4中可运移氡产生率所对应的理论计算值。由图4可见,同一高度处孔隙氡活度浓度随渗流速度或压力梯度的增大近似呈负指数减小。

图4 破碎射气介质内不同高度处孔隙氡活度浓度随渗流速度的变化
3.4 破碎射气介质表面氡析出率的变化规律
在实验所给的渗流速度范围内,破碎射气介质中氡主要以渗流方式迁移。因此,在计算介质不同高度处截面的氡通量时,可不考虑氡的扩散迁移通量,其计算式为:
Γ=vc(x)A
(9)
式中,Γ为介质不同高度处截面的氡通量,Bq·s-1。
则介质表面的氡析出率为:

式中,h为介质的高度,对于本实验h=2.5m。
利用表2中的实测数据,按式(3)所给出的数学关系对孔隙氡活度浓度与渗流速度和孔隙高度进行多元拟合,得到可运移氡产生率α=4.348Bq·m-3·s-1,相关系数R=0.998 6。依据式(10)计算出一定渗流速度范围内本实验矿样表面的氡析出率,并与实测值进行比较,结果示于图5。

图5 介质表面氡析出率随渗流速度的变化
由图5可见,对于高度一定的破碎介质,介质表面氡析出率随着渗流速度增大而逐渐增大,但增长速率逐渐变缓,最终稳定在一极限值以下。同时通过计算可知,渗流速度为0.954 9×10-4、1.273 2×10-4、1.485 4×10-4、2.546 5×10-4、3.183 1×10-4、6.366 2×10-4、1.697 7×10-3m/s时,介质表面氡析出率的实测值与式(10)计算值之间的相对偏差分别为:1.86%、0.22%、0.18%、0.25%、0.58%、0.58%、0.05%。此结果表明,当渗流速度较大时,可用式(10)研究不同渗流速度下破碎射气介质表面氡析出率的变化规律。
4 结论
利用自制的一维渗流实验装置,对7个不同渗流速度下破碎射气介质内孔隙氡活度浓度以及介质表面氡析出率的变化规律进行了实验研究,得到以下结论。
1)空气在破碎射气介质内的渗透率较大,当有限厚破碎射气介质两侧存在压力梯度时,介质内氡运移很容易由渗流主导。
2)当破碎射气介质内氡运移由渗流主导时,氡的扩散作用可忽略。此时,可通过测量破碎射气介质同一位置不同渗流速度下的孔隙氡活度浓度或同一渗流速度不同位置处的孔隙氡活度浓度,再联合仅考虑渗流迁移作用下射气介质内氡的浓度分布解析式及其非线性最小二乘法,估算出介质的可运移氡产生率。
3)一定渗流速度范围内,破碎射气介质内的孔隙氡活度浓度随介质增高近似呈线性增大,随渗流速度或压力梯度的增大呈负指数减小;介质渗流出口表面氡析出率随渗流速度或压力梯度的增大而增大,最终趋于稳定。
[1] KREWSKI D,LUBIN J,ZIELINSKI J,et al.Residential radon and risk of lung cancer:A combined analysis of 7North American case-control studies[J].Epidemiology,2005,16(2):137-145.
[2] TOMASEK L,DARBY S C,FEARN T,et al.Patterns of lung cancer mortality among uranium miners in west bohemia with varying rates of exposure to radon and its progeny[J].Radiation Research,1994,137(2):251-261.
[3] TOMASEK L.Radon exposure and cancers other than lung cancer among uranium miners in West Bohemia[J].GBR-Lancet,1993,34:919-923.
[4] KUSIAK R A.Mortality from lung cancer in Ontario uranium miners[J].British Journal of Industrial Medicine,1993,50(10):920-928.
[5] DARBY S,HILL D,AUVINEN A,et al.Radon in homes and risk of lung cancer:Collaborative analysis of individual data from 13European case-control studies[J].Br Med J,2005,330:223-226.
[6] DARBY S C,ELISE W,HOWE G R.Lung cancer in radon-exposed miners and estimation of risk from indoor exposure[J].Journal of the Na-tional Cancer Institute,1995,87(5):378-384.
[7] 张哲.氡的析出与排氡通风[M].北京:原子能出版社,1982.
[8] ROGERS V C,NIELSON K K.Multiphase radon generation and transport in porous materials[J].Health Physics,1991,60(6):807-815.
[9] 何斌,过惠平,尚爱国.对计算土壤和岩石中氡浓度及其表面析出率表面边界条件的讨论[J].铀矿地质,1998,14(5):302-306.HE Bin,GUO Huiping,SHANG Aiguo.Discussion boundary conditions for calculating radon concentration sand surface exhalation rates in soil and rock[J].Uranium Geology,1998,14(5):302-306(in Chinese).
[10]孙凯男.土壤氡析出率的研究[D].北京:清华大学,2004.
[11]YAKOVLEVA V S,PAROVIK R I.Solution of diffusion-advection equation of radon transport in many-layered geological media[J].Nukleonika,2010,55(4):601-606.
[12]申超,陈凌,肖徳涛,等.不同土壤氡分布的数值模拟[J].原子能科学技术,2012,46(3):370-374.SHEN Chao,CHEN Ling,XIAO Detao,et al.Numerical computation of radon distribution in different soil[J].Atomic Energy Science and Technology,2012,46(3):370-374(in Chinese).
[13]曹众为,李向阳,叶勇军,等.压力梯度对多孔介质氡析出率影响的试验研究[J].铀矿冶,2013,32(1):38-41.CAO Zhongwei,LI Xiangyang,YE Yongjun,et al.Experimental study on influence of pressure gradient on radon exhalation from porous medium[J].Uranium Mining and Metallurgy,2013,32(1):38-41(in Chinese).
[14]张哲,朱民安,张永祥,等.地下工程与人居环境氡防护技术[M].北京:原子能出版社,2010.
[15]李广悦,丁德馨,陈翔,等.松散破碎射气介质氡析出能力的测量与计算[J].核科学与工程,2010,30(4):380-384.LI Guangyue,DING Dexin,CHEN Xiang,et al.Measurement and calculation for radon emanation capability of loose fragmented radon-emitting medium[J].Chinese Journal of Nuclear Science and Engineering,2010,30(4):380-384(in Chinese).

