统计收敛与超滤子收敛的关系
林丽华,鲍玲鑫
(1.三明学院信息工程学院,福建 三明 365004;2.福建农林大学计算机与信息学院,福建 福州 350002)
1951年,Fast[1]和Steinhaus[2]分别独立地引入了统计收敛的定义:称实值序列(xn)统计收敛于a∈R,如果对∀ε>0,都有
其中A#表示集合A的势.显然这是数列通常意义下收敛的推广.
之后,统计收敛问题得到Connor[3]、Fridy[4-6]、Miller[7]、Bal-cerzak[8]、Das[9]等人的深入研究.值得注意的是,自20世纪90 年代以来对统计收敛的性质以及各种在统计收敛概念的基础上,再次推广的概念与性质的研究异常活跃,成为人们研究的热点问题,在各个纯数学和应用数学领域进行了广泛的讨论和深入的研究.其讨论涉及矩阵求和、级数理论、傅里叶分析、三角级数论、Banach空间理论、局部凸空间以及模糊数学等等诸多领域.
2008年程立新等[10]建立了统计收敛的测度理论,并在此基础上将每一类型的统计收敛都用统一的统计测度来刻画[11].最近程立新与鲍玲鑫[12]给出了统计测度与统计收敛中最为一般的收敛形式——理想收敛之间的关系.本文在此基础上进一步讨论统计测度收敛与超滤子收敛的关系.
为了读者的阅读方便,先将在本文中统计收敛理论中常用的记号简述如下:
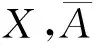
A(ε,x,xn)={n∈N:‖xn-x‖>ε},
在不至于混淆情况下,简记为A(ε).
1 超滤子、端点与有限可加退化概率测度之间的关系
本节将给出超滤子、端点与有限可加退化概率测度的关系.为此首先回顾一些基本的概念.
设(Ω,Σ)为一测度空间,其中Ω为一非空集合,Σ⊂2Ω是一σ-代数.称函数μ:Σ→R+为Σ上的有限可加概率测度,如果它满足条件:(i)μ(φ)=0且μ(Ω)=1;(ii) 对任意的A,B∈Σ,当A∩B=φ时,有μ(A∪B)=μ(A)+μ(B).
另外,μ若还满足:1) 对∀A∈Σ,μ(A)=0或者μ(A)=1,则称μ为定义在Σ上的有限可加退化概率测度;2) 对于Σ中的单点集{x}有μ({x})=0,则称μ为定义在Σ上的统计测度.
滤子与理想是一对互补的概念.设Ω是一个非空集合,2Ω是集合Ω的幂集,F⊂2Ω,若F满足:(i)φ∉F;(ii) 若A∈F,B∈F,则A∩B∈F;(iii) 若A⊂B⊂Ω,A∈F,则B∈F,则称F为集合Ω上的滤子.显然如果Ω是非空集,易得F={Ω}就是一个Ω上的滤子.所以对任何非空集Ω,都可谈论Ω上的滤子.集合Ω上的一个滤子F若满足:对于集合Ω上的其他滤子F1,当F⊂F1时,有F=F1,则称F为集合Ω的一个超滤子.超滤子有一个很好的特征性质,即F是集合Ω上的一个超滤子的充分必要条件是对任何A⊂Ω,有下列条件之一且只有之一成立:A∈F,或ΩA∈F.
本文中考虑Ω=N,以及Σ=2N的情况.这里我们先给出l∞中两元素乘积的形式表达式.
若记x={x1,x2,…xn,…}∈l∞,y={y1,y2,…yn,…}∈l∞,本文中的x·y是指x·y={x1y1,x2y2,…,xnyn,…},易知x·y∈l∞.
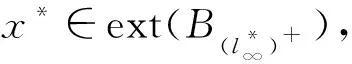

即式(1)成立.
接着考虑,当x,y中有一个范数小于1时的情形.

有
类似的有
y>≥0. 又由于 1+ 所以我们有x*±y*∈(B(l∞)*+),又x*∈ext(B(l∞)*+),故y*=θ.于是由y的任意性即得:当x,y∈l∞中有一个满足范数小于1时式(1)成立. s s μ(A)= (2) 则由于χA(i)≥0,i∈N,x*是正泛函,故有μ(A)≥0,且有μ(φ)= 另外,若A,B∈2N且A∩B=φ,则有 μ(A∪B)= 综上所述知,由式(2)定义的测度是一个有限可加测度. 由引理1,∀A∈2N,有 0= χA>· (1- 即 下面证明,上述的有限可加退化概率测度μ可定义一个2N上的超滤子. 事实上,令U={A|A∈2N,μ(A)=1},则U就是一个由测度μ确定的超滤子.首先由1=μ(N)=μ(φ∪N)=μ(φ)+μ(N)=1+μ(φ),可得μ(φ)=0,即φ不属于U;若设A∈U,B∈U,则由 μ(NA)+μ(NB)=0, 又若A∈U,由 1=μ(N)=μ(A∪(NA))= μ(A)+μ(NA)=1+μ(NA), 有μ(NA)=0,即NA∉U,这也就说明了A与NA有且仅有一个属于U,于是由超滤子的性质知,此时的U={A|A∈2N,μ(A)=1}就是一个由测度μ确定的超滤子. 定理2 设U⊂2N为一个超滤子,若通过下式定义函数μ:2N→R, (3) 证明由于U⊂2N是超滤子,故N∈U,φ∉U,于是μ(N)=1,μ(φ)=0. 若A,B∈2N且A∩B=φ,则由φ∉U知A,B至少有一个不属于U,于是易得 μ(A∪B)=μ(A)+μ(B), 即满足有限可加性,所以由式(3)定义的测度μ是定义在2N上的有限可加概率测度. 故由下式 有了以上的超滤子、端点和退化的有限可加概率测度的关系,下面可以给出统计测度收敛与超滤子收敛之间的等价关系.为此先给出一个定义. 定义1[12]设ω是定义在(N,2N)上的一个统计测度族,x∈X,A∈2N,(xn)⊂X. (i) 若∀μ∈ω,有μ(A)=0,则称A为ω-零集; (ii) 若∀ε>0,A(ε)是一个ω-零测集,则称(xn)ω-测度收敛于x. μ(A)= 则此时定义的测度是取值为{0,1}的统计型有限可加概率测度. 令U={A|A∈2N,μ(A)=1},则U是由测度μ确定的超滤子.于是若序列(xn)按x*所确定的测度收敛于x,即 μ({n∈N,‖xn-x‖≥ε})=0或μ({n∈N, ‖xn-x‖<ε})=1, 则{n∈N,‖xn-x‖<ε}∈U,于是序列(xn)超滤子收敛于x. 反之,若序列(xn)超滤子收敛于x,即{n∈N,‖xn-x‖<ε}∈U,则有 μ({n∈N,‖xn-x‖<ε})=1, 即μ({n∈N,‖xn-x‖≥ε})=0,于是序列(xn)按x*所确定的测度收敛于x. 由以上容易得出如下推论. 推论1 设X是一个Banach空间,ω={μ,μ(A)= [1] Fast H.Sur le convergence statistical[J].Colloq Math,1951,2(1):241-244. [2] Steinhaus H.Sur la convergence ordinaire et la convergence asymptotique[J].Colloq Math,1951,2(2):73-74. [3] Connor J.Two valued measure and summability[J].Analysis,1990,10(4):373-385. [4] Fridy J A.On statistical convergent[J].Analysis,1985,5(4):301-313. [5] Fridy J A.Statistical limit points[J].Proceedings of the American Mathematical Society,1993,118(4):1187-1192. [6] Fridy J A,Orhan C.Lacunary statistical summability[J].Journal of Mathematical Analysis and Applications,1993,173(2):497-504. [7] Miller H I,Orhan C.On almost convergent and statistically convergent subsequences[J].Acta Mathematica Hungarica,2001,93(1/2):135-151. [8] Balcerzak M,Dems K,Komisarski A.Statistical convergence and ideal convergence for sequences of functions[J].Journal of Mathematical Analysis and Applications,2007,328(1):715-729. [9] Das P,Savas E,Ghosal S K.On generalization of certain summability methods using ideals[J].Applied Mathematics Letters,2011,24(9):1509-1514. [10] Cheng L X,Lin G C,Lan Y Y,et al.Measure theory of statistical convergence[J].Science China:Series A,2008,51(12):2285-2303. [11] Cheng L X,Lin G C,Shi H H.On real-valued measures of statistical type and their applications to statistical convergence[J].Mathematical and Computer Modelling,2009,50(1/2):116-122. [12] Bao L X,Cheng L X.On statistical measure theory[J].Journal of Mathematical Analysis and Applications,2013,407:413-424. [13] 俞鑫泰.Banach空间几何理论[M].上海:华东师范大学出版社,1986.
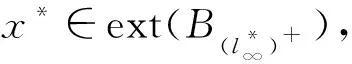
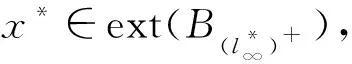
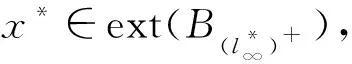


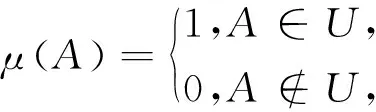





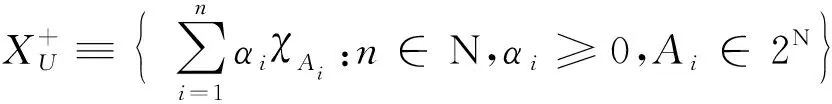

2 统计测度收敛与超滤子收敛