单层二硫化钼光学性质的第一性原理计算
杨志鹏,吴顺情,文玉华,朱梓忠
(厦门大学物理与机电工程学院,福建 厦门 361005)
二硫化钼(MoS2)作为典型的过渡金属层状二元化合物,其热稳定性和化学稳定性良好,被广泛应用于固体润滑剂[1-5]、电极材料[6-7]和反应催化剂[8-9]等领域.早在1986年,就有人通过插入锂的方法成功剥离出单层MoS2[10].近年来,通过溶剂[11]或裂解[12]的方法制备单层MoS2的方法也有报道.如今,作为典型的类石墨烯单层过渡金属化合物,单层MoS2凭借其优秀的光学和电学性质在辅助石墨烯甚至替代石墨烯上有着很好的前景,在晶体管制造[13]和电子探针的应用[14]等方面也受到人们的关注.
MoS2是间接带隙半导体材料,其禁带宽度为1.29 eV[15],而单层MoS2则是直接带隙半导体材料,禁带宽度为1.8 eV[11].到目前为止,对于MoS2体材料的电子结构和表面性质有了大量的理论和实验研究,但是对其光学性质,尤其是单层MoS2的光学性质的研究还比较少.近年来,基于密度泛函(DFT)理论的第一性原理方法越来越多地被运用于计算材料的光学性质.本文中,我们采用DFT理论框架下的缀加投影平面波方法,使用局域密度近似,对单层MoS2的能带结构、态密度及光学性质如能量损失谱、吸收系数、反射率、折射率和消光系数等进行了比较全面的计算,并将结果与现有的理论结果相比较.
1 计算方法
本文的计算采用基于DFT理论的第一性原理方法,使用的程序包是Vienna ab initio simulation package(VASP)[16-17].该程序包采用平面波展开,映射缀加波势(projector augmented-wave potentials,PAW)[18]以及局域密度近似(LDA)形式的交换关联势[19].计算时平面波截断能量为360 eV,所有结构均弛豫至原子间作用力小于1×10-4eV/nm.布里渊区的积分采用Monkhost-Pack特殊k点取样方法[20],对于单层MoS2,选取了7×7×1的k-网格.计算时使用超原胞和周期性边界条件,单原子层薄片方向为x、y方向,z方向取为300 nm厚的真空层,以消除原子薄片间的相互作用.
MoS2属于简单六角结构(见图1(a)).体结构的MoS2晶体在自然界中自然存在,层与层之间由范德瓦尔兹力联系.MoS2(2H-MoS2)体材料是由两层S原子与一层Mo原子堆叠形成的三明治状的层状结构相对堆叠而成的(见图1(b)).当联系层与层间的键被切断时,体材料的MoS2便切割为单层MoS2(1H-MoS2,如图1(b)).MoS2属于单轴晶体,其结构在平行于a轴方向与平行于b轴方向上完全相同,但在c轴方向上(图1(a))则与前二者不同.因此,在计算的时候,可以将电矢量E区分为垂直于c轴(Ec⊥(ω))和平行于c轴(Ec∥(ω))2个方向进行计算.
计算获得的单层MoS2的晶格常数为a=b=0.312 nm,Mo与S之间形成共价键的键长为0.241 1 nm,S—Mo—S之间形成的较大的键角为80.94°,较小的键角为46.21°,与文献[21]的研究结果非常相近.
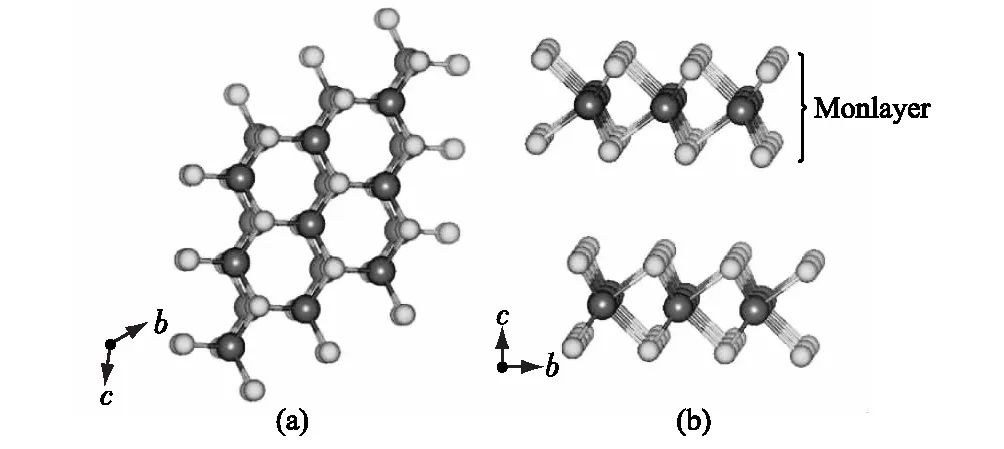
图1 MoS2体材料的顶视图(a)和侧视图(b)Fig.1 Top view of bulk MoS2(a) and side view of bulk MoS2(b)
2 计算结果及讨论
图2(a)给出了单层MoS2的电子能带结构.可以看出,-12~-14 eV范围内的能带主要来自S原子的s电子的贡献.其他的价带则主要分布在-6 eV到费米能级的范围内,其能带以Mo-d态及S-p态杂化的贡献为主.费米能级以上的能带主要为Mo-d态及S-p态杂化的反键态.从能带图中还可以看到,单层MoS2呈现为直接带隙,价带顶和导带底都位于K对称点上,带隙宽度为1.71 eV.相较于体材料MoS2的间接带隙1.29 eV[15],单层MoS2禁带宽度更大一些.出现这一差别的原因是对于单层的MoS2不存在层与层之间的范德瓦尔兹力.图2(b)给出了单层MoS2的电子分态密度图.可以看出,单层MoS2的分态密度与体材料非常接近,只有带隙宽度及附近有所不同.
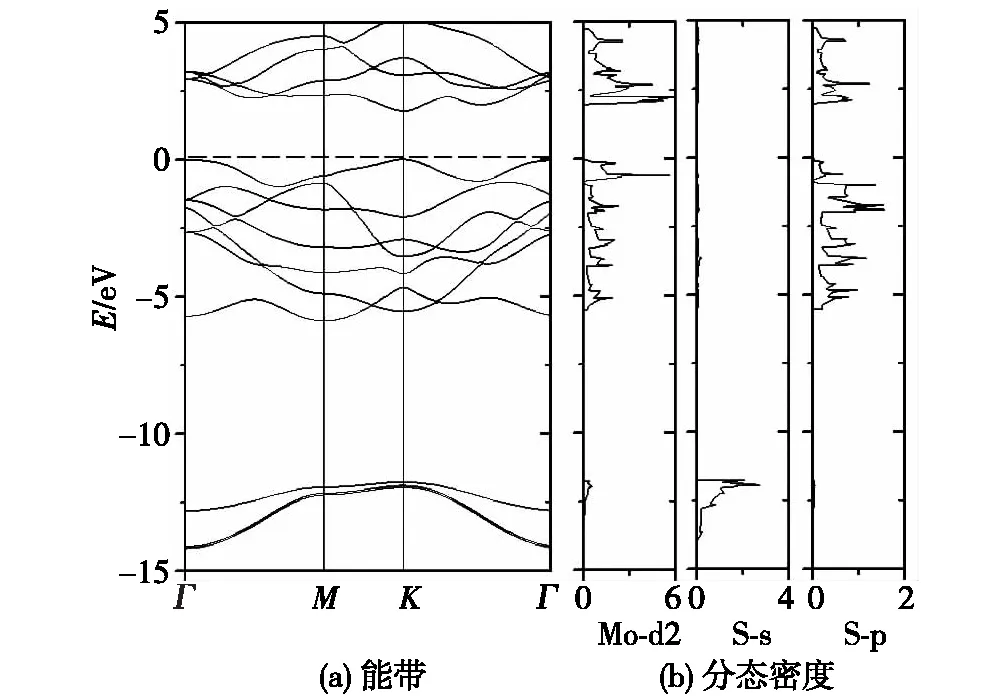
图2 单层MoS2的能带(a)和分态密度(b)Fig.2 Band structure (a) and DOS for single-layer MoS2 (b)
在能带计算的基础上,对体材料和单层MoS2的光学性质都进行了计算.介电函数ε(ω)是一个虚数,由实部和虚部两部分组成:
ε(ω)=ε1(ω)+iε2(ω),
(1)
介电函数的虚数部分ε2(ω)可以通过对能带的计算得到[22]:

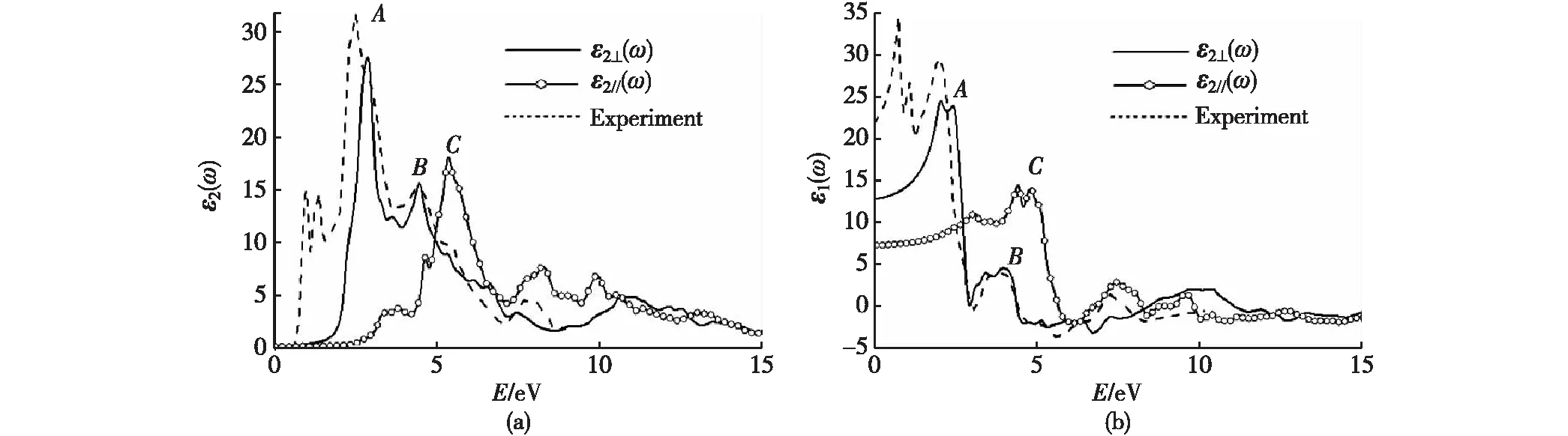
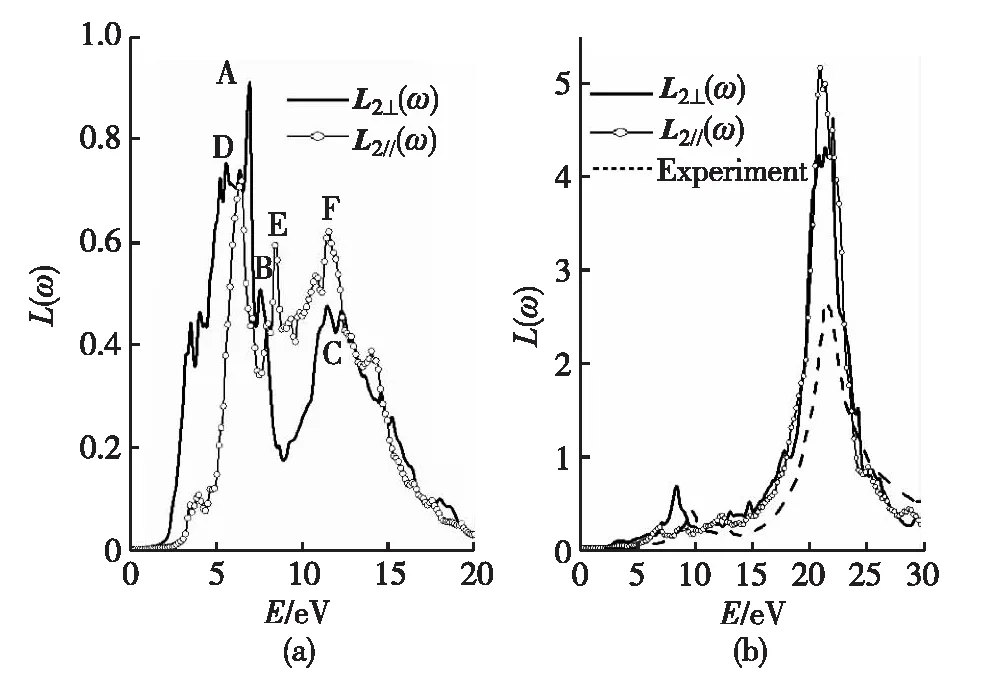
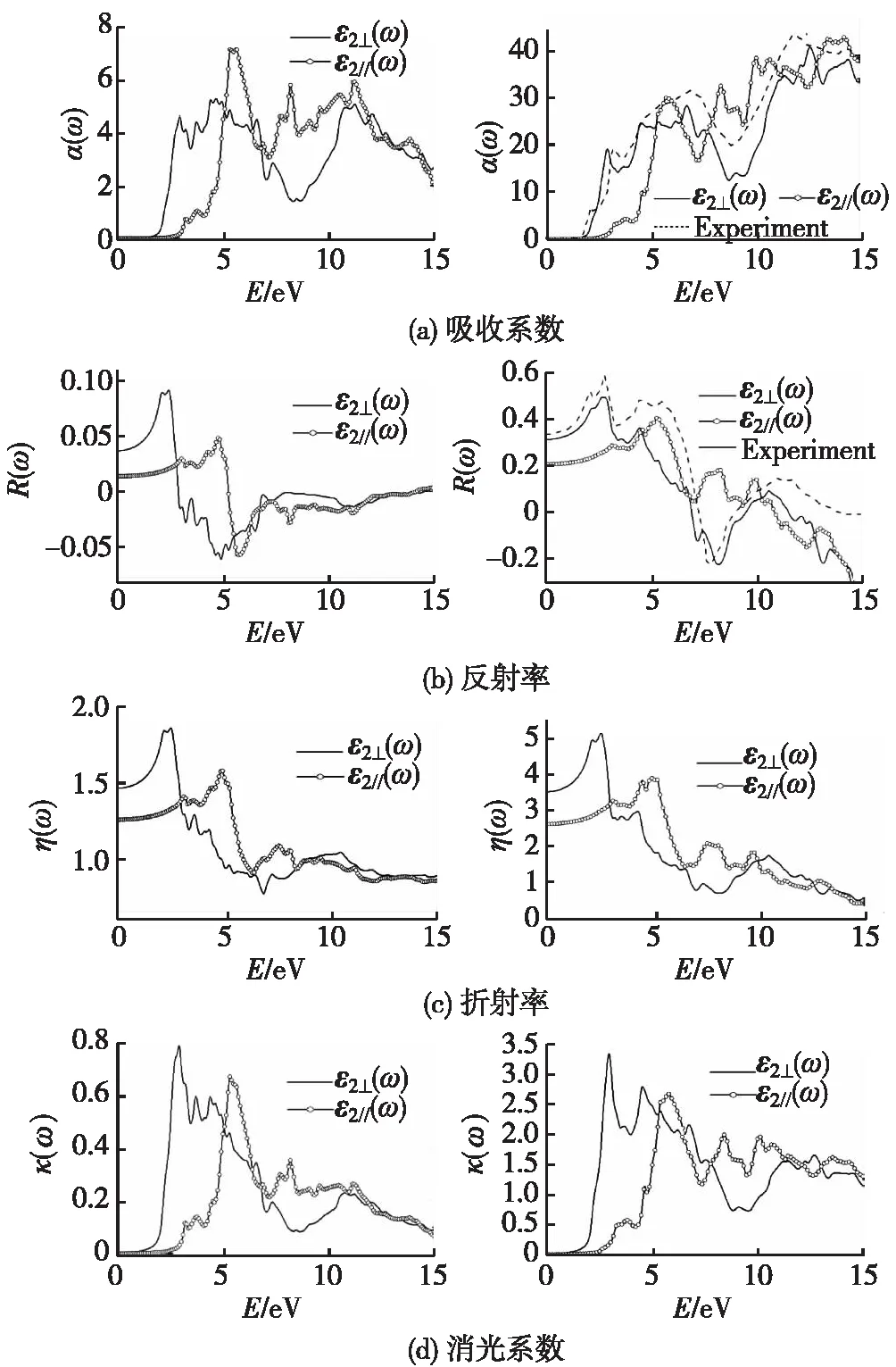
kβ|uvk>*, (2) 而介电函数的实数部分ε1(ω)则由虚部ε2(ω)通过Kramer-Kronig变换得到[22]: (3) 介电函数ε(ω)是一个二阶张量,对于简单六角结构,介电函数分为平行及垂直于c轴2个方向的2个部分. 垂直于c轴方向: (4) 平行于c轴方向: ε∥(ω)=εzz(ω), (5) 此处εxx(ω)、εyy(ω)及εzz(ω)为二阶张量矩阵中的矩阵元εij(ω).由于MoS2是单轴晶体,因此ε⊥(ω)=εxx(ω)=εyy(ω),且εij(ω)=0(i≠j). 单层MoS2的介电函数在图3中给出.图3(a)给出了单层MoS2的介电函数虚数部分.ε2⊥(ω)及ε2∥(ω)的图像在7 eV以下(低能量范围内)差距较大,在7 eV以上(高能量范围内)比较接近.ε2⊥(ω)的峰值出现在2.7 eV(图中标示为A)、3.68 eV(B)及4.35 eV(C)处,相较于体材料MoS2多出了一个位于3.68 eV的峰值,此峰值在体材料MoS2中仅表现为一个小的突起.峰A是由费米能级EF下方的第1条价带向EF上方的第1条导带的跃迁(Γ→M方向)的贡献决定的;峰B则由第2价带向第2导带的带间跃迁(Γ→M方向)决定的;峰C的贡献则来自于第2和第3价带向第3和第4导带的带间跃迁(Γ→M→K方向).ε2∥(ω)仅表现出一个峰D(5.3 eV),它是由第4和第5价带向第1和第2导带的带间跃迁决定的. 图3 单层MoS2介电函数的虚部ε2(a)和实部ε1(b)Fig.3 The imaginary part ε2(a) and the real part ε1(b) of dielectric function of single-layer MoS2 单层MoS2的介电函数实数部分ε1⊥(ω)及ε1∥(ω)在图3(b)中给出.介电函数的实数部分是由虚数部分通过Kramer-Kronig变换得到的,并在式(3)中加入几个大小为0.1的复数漂移.ε1⊥(ω)在2.17 eV(A)及3.56 eV(B)处分别出现峰值,而ε1∥(ω)的峰值出现在4.83 eV(C)处.ε1⊥(ω)与ε1∥(ω)的图像在6 eV以下(低能量范围)差别较大,在6 eV以上(高能量范围)差别较小.当能量等于0时,介电函数的虚数部分ε2(ω)=0,此时介电函数的值称为静态介电常量,记为ε0.我们计算了单层MoS2的静态介电常数,分别为ε0⊥(ω)=2.17及ε0∥(ω)=1.62. 图4 MoS2体材料介电函数的虚部(a)和实部(b)Fig.4 The imaginary part ε2 (a) and the real part ε1 of dielectric function of bulk MoS2 (b) 图4(a)给出了体材料MoS2的介电函数的虚数部分ε2⊥(ω)及ε2∥(ω).体材料与单层MoS2在峰的位置及曲线的走向上都很类似,但是在谱峰的高度上单层MoS2要高一些.可以看到,介电函数虚部垂直于c轴的部分及平行于c轴的部分在约6 eV之前(低能量范围内)差别较大,而在6 eV之后(高能量范围内)趋于接近.ε2⊥(ω)部分在3 eV(A)及4.5 eV(B)附近表现出明显的峰值,而ε2∥(ω)的峰值出现在5.5 eV(C)附近.与实验结果相比较可以看出,ε2⊥(ω)部分与实验符合较好,但是在峰的位置上整体有一个约0.5 eV的偏移.谱峰的位置由能带带间跃迁决定,峰A主要由EF下方的第1、2条价带向EF上方第5、6条导带(Γ→M方向)的跃迁以及EF下方第2条价带向EF上方的第3、4条导带(K→Γ方向)的跃迁所决定;峰B主要来自于EF下方第5,6条价带向EF上方第3、4条导带(M→K→Γ方向)的带间跃迁贡献;峰C则主要由EF下方第7,8条价带向EF上方第1,2条导带(M→K→Γ方向)的带间跃迁决定. MoS2体材料介电函数的实数部分ε1⊥(ω)及ε1∥(ω)在图4(b)中给出.对于实数部分,ε1⊥(ω)及ε1∥(ω)同样在6 eV以下(低能量范围内)呈现较大的区别,在6 eV以上(高能量范围内)趋于接近.ε1⊥(ω)在2.2 eV(A)及4.1 eV(B)处分别表现出一个双峰,ε1∥(ω)的峰值则出现在4.5 eV(C)附近.实验结果与ε1⊥(ω)符合较好,但没有在4.1 eV处表现出峰值,仅出现一个小的坡度变化.对于体材料MoS2,静态介电常数ε0⊥(ω)=12.78,ε0∥(ω)=7.22. 目前还没有成功制备脱离衬底或溶剂的独立单层MoS2薄片的报导,因此对于单层MoS2的光学测试和观测都比较困难.我们对于单层MoS2的光学性质进行了比较详尽的计算,并计算了体材料MoS2的相关性质给予对比.对于单层MoS2,在这里我们主要考虑入射光平行于c轴方向的情况.各项光学常数随着入射光频率的变化而变化,这一现象称之为色散现象.固体的能量吸收谱L(ω)、吸收系数α(ω)、折射率n(ω)、反射率R(ω)以及消光系数κ(ω)的色散关系都可以通过对介电函数实部ε1(ω)与虚部ε2(ω)的计算得到.其计算关系式[23]在下面给出: (6) (7) (8) (9) (10) 我们分别对单层MoS2和体材料的上述光学性质进行了计算.单层MoS2的能量吸收谱在图5(a)中给出.单层MoS2的L⊥(ω)分别在6.76 eV(A)、7.38 eV(B)以及11.29 eV(C)处形成峰,L∥(ω)的峰则出现在6.27 eV(D)、8.29 eV(E)及11.36 eV(F)处.图5(b)给出了体材料MoS2的能量吸收谱.体材料的L⊥(ω)与L∥(ω)的图像基本一致,L⊥(ω)在21.55 eV处峰值最高,而L∥(ω)的峰值则分别出现在21.08 eV及22.25 eV处.相较于文献[24]中体材料的实验结果,我们计算得出的结果峰值更高些.相较于体材料,单层MoS2的曲线表现出更大的波动,峰的数量更多且不再在低能量范围内表现平缓,总之与体材料MoS2的能量吸收谱差别较大. 图5 MoS2单层(a)和MoS2体材料的能量吸收谱(b)Fig.5 The engery loss spectrum of single-layer MoS2 (a) and bulk MoS2 (b) 图6 MoS2单层(左图)和体材料(右图)的各个光学性质Fig.6 Optical properties of single-layer (left) and bulk (right) MoS2 单层及体材料MoS2的其他光学性质(包括吸收系数、折射率、反射率及消光系数等)在图6中给出.图6(a)是MoS2单层及体材料的吸收系数α(ω)的曲线.可以看到,体材料数据与文献[25]的实验曲线符合较好.吸收系数在8.69 eV处有一个低谷,峰值位置出现在12.66 eV处.由单层MoS2的α∥(ω)曲线可以看出,单层MoS2的吸收系数很低,对可见光(1.64~3.19 eV内)吸收作用小,因此独立的单层MoS2薄片应是透明的.单层MoS2的α∥(ω)曲线在5.5 eV附近达到峰值,说明其对红外线的吸收作用较大.图6(b)给出了MoS2单层和体材料的反射率曲线.体材料数据与文献[26]的实验数据符合良好.在可见光波段内体材料的反射率曲线维持在0.3~0.4左右,证明体材料MoS2可以反射约30%~40%的入射光,并呈现出金属光泽.而单层MoS2薄片的R∥(ω)在可见光波段的值约为0.01~0.02,故应为暗淡无金属光泽的.图6(c)给出单层及体材料MoS2的折射率曲线.单层及体材料MoS2的折射率曲线形态相近,但数值相差较大.单层MoS2的n∥(ω)曲线在可见光范围内维持在1.3左右,与水的折射率1.33相近.这也同样说明,独立的单层MoS2薄片应是透明的.图6(d)给出单层和体材料MoS2的消光系数曲线.体材料及单层MoS2的消光系数曲线均在3 eV左右达到最高值,之后随着入射光频率的增高趋近于0,说明随着入射光光子频率的增加,MoS2材料越来越趋于透明. 本文使用基于DFT理论的第一性原理方法计算了单层以及体材料MoS2的能带结构、态密度以及各个光学性质,并将体材料MoS2的介电函数、能量吸收谱、吸收系数及反射率等光学性质与实验数据进行了比较,理论计算与实验数据符合较好.计算表明,单层MoS2与其体材料由于结构上的类似,因此在许多性质上有相近的地方,主要表现在各光学性质的变化趋势上(尽管在各光学性质的数值上单层MoS2明显小于体材料).对于单层MoS2,由于层间不再具有范德瓦尔兹力,导致单层MoS2与体材料MoS2的介电函数存在一定差异.而范式力的缺失另一方面也表现在单层MoS2与体材料MoS2电子结构上的不同,单层的MoS2呈现为直接带隙,禁带宽度为1.71 eV,而体材料MoS2呈现为禁带宽度为1.54 eV的间接带隙材料.我们也指出了体材料及单层MoS2介电函数图像中各峰值与对应的能带带间跃迁之间的关系,可以为实验上进一步研究MoS2的光学性质提供参考.通过对单层MoS2光学性质的一系列计算,我们还推断单层的MoS2薄片应属于透明无色无金属光泽的薄片,并随着入射光频率的增加变得越来越容易穿透. [1] Winer W O.Molybdenum disulfide as a lubricant:a review of the fundamental knowledge[J].Wear,1967,10(6):422-452. [2] Brudnyi I,Karmadonov A F.Structure of molybdenum disulphide lubricant film[J].Wear,1975,33(2):243-249. [3] Farr J P G.Molybdenum disulphide in lubrication,a review[J].Wear,1975,35(1):1-22. [4] Fleischauer P D,Lince J R,Bertrand P A,et al.Electronic structure and lubrication properties of molybdenum disulfide:a qualitative molecular orbital approach [J].Langmuir,1989,5(4):1009-1015. [5] Martin J M,Donnet C,Le Mogne T,et al.Superlubricity of molybdenum disulphide[J].Phys Rev B,1993,48(14):10583-10586. [6] Rapport L,Bilik Y,Homyonfer M.Hollow nanoparticles of WS2as potential solid-state lubricants[J].Nature,1997,387(6635):791-793. [7] Xiao J,Choi D,Cosimbescu L,et al.Exfoliated MoS2nanocomposite as an anode material for lithium ion batteries[J].Chemistry of Materials,2010,22(16):4522-4524. [8] Srivastava S K,Avasthi B N.Preparation and characterization of molybdenum disulphide catalysts[J].Journal of materials science,1993,28(18):5032-5035. [9] Mdleni M M,Hyeon T,Suslick K S.Sonochemical synthesis of nanostructured molybdenum sulfide[J].Journal of the American chemical society,1998,120(24):6189-6190. [10] Joensen P,Morrson S R.Single-layer MoS2[J].Materials research bulletin,1986,21(4):457-461. [11] Novoselov K S,Jiang D,Schedin F,et al.Two-dimensional atomic crystals[J].Proceedings of the National Academy of Sciences of the United States of America,2005,102(30):10451-10453. [12] Colema J N,Lotya M,O'Neill A,et al.Two-dimensional nanosheets produced by liquid exfoliation of layered materials[J].Science,2011,331(6017):568-571. [13] 赖占平.二维辉钼材料及器件研究进展[J].物理学报,2013,62(5):056801. [14] Homyonfer M,Alperson B,Rosenberg Y.Intercalation of inorganic fullerene-like structures yields photosensitive films and new tips for scanning probe microscopy[J].Journal of the American Chemical Society,1997,119(11):2693-2698. [15] Mak K F,Lee C,Hone J,et al.Atomically thin MoS2:a new direct-gap semiconductor[J].Physical Review Letters,2010,105(13):136805. [16] Kresse G,Furthmüller J.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Physical Review B,1996,54(16):11169-11186. [17] Kresse G,Furthmüller J.Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J].Computational Materials Science,1996,6(1):15-50. [18] Kresse G,Joubert D.From ultrasoft pseudopotentials to the projector augmented-wave method[J].Physical Review B,1999,59(3):1758-1775. [19] Perdew J P,Zunger A.Self-interaction correction to density-functional approximations for many-electron systems[J].Physical Review B,1981,23(10):5048-5079. [20] Monkhorst H J,Pack J D.Special points for Brillouin-zone integrations[J].Physical Review B,1976,13(12):5188-5192. [21] Ramakrishna Matte H S S,Gomathi A,Manna A K,et al.MoS2and WS2analogues of graphene[J].Angewandte Chemie,2010,122(24):4153-4156. [22] Gajdoš M,Hummer K,Kresse G,et al.Linear optical properties in the projector-augmented wave methodology [J].Physical Review B,2006,73(4):045112. [23] 方容川.固体光谱学[M].合肥:中国科学技术大学出版社,2001. [24] Johari P,Shenoy V B.Modulating optical properties of graphene oxide:role of prominent functional groups[J].ACS Nano,2011,5(9):7640-7647. [25] Beal A R,Hughes H P.Kramers-Kronig analysis of the reflectivity spectra of 2H-MoS2,2H-MoSe2and 2H-MoTe2[J].Journal of Physics C:Solid State Physics,1979,12(5):881-890. [26] Liang W Y.Reflectivity of MoS2and NbSe2[J].Journal of Physics C:Solid State Physics,1971,4(18):378-381.
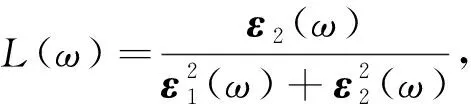
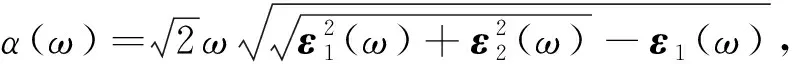
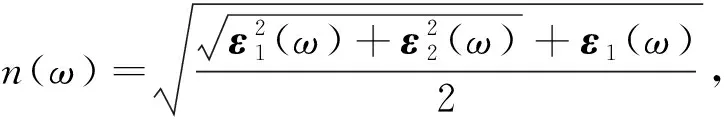
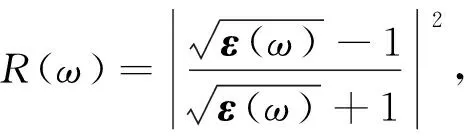
3 结 论
- 厦门大学学报(自然科学版)的其它文章
- 空间分数阶Klein-Gordon方程的一种有效数值算法
- 统计收敛与超滤子收敛的关系
- 关于可逼近性和弱紧性的一个注记

