基于双种群交流粒子群算法的离散投资组合模型

王秀利，刘 洋

中央财经大学 信息学院，北京 100081

基于双种群交流粒子群算法的离散投资组合模型

王秀利，刘 洋

中央财经大学 信息学院，北京 100081

1 引言

均值-方差模型[1]寻求在一定收益水平下风险最小，或在一定风险水平下收益最大。但该模型基于一系列严格假设，与实际证券市场投资环境存在很大差异，因此，考虑买空卖空限制、整数手数交易、交易费用等实际因素，提出一种符合当前我国证券投资市场的更完善的投资组合模型。其求解方法有人工神经网络方法[2]、进化算法[3]、模糊系统[4]等，这些算法需要交叉、变异等特殊处理操作或对目标函数的特征有着严格要求。

粒子群算法（Particle Swarm Optimization，PSO）无需交叉、变异，对目标函数无特殊要求，被广泛应用于模糊系统控制、神经网络训练、函数优化、工程应用[5-6]中，但其后期收敛速度慢，面对多极值问题时容易陷入局部最优。其改进算法有以下几种：将不同的算法与PSO嵌入，优势互补[7-8]；采用新的学习策略更新位置和速度[9]；改变搜索环境或搜索状态[10]等。

用改进PSO算法求解投资组合问题取得了很多成果，但也存在不足之处，如文献[11]将捕食策略引入PSO，提高了搜索精度，但增大了时间复杂度，同时算法最终可能出现不可能解，投资组合模型中忽略了投资者偏好；文献[12]引入遗传算法提高了PSO算法的搜索性能，并能够找到风险更小的投资组合，但新算法因复杂的“交叉”操作而使PSO失去了简单易行的最大优势，并且没有考虑完整的交易费用等实际因素；与本文相似，文献[13]同样在标准PSO中引入了两个种群，但是学习过程中粒子的行动受到速度范围的制约，跳出局部极值的可能性很小，很可能学习失败，且速度的变异方式无根据可循。

本文以被学习种群作为标尺，由学习种群根据一定标准进行速度变异从而向新区域探索，不改变空间复杂度，收敛速度更快，精度更高。本文把基于双种群交流的离散PSO算法应用于符合我国实际情况的证券投资组合模型中，实现了最优化求解。

2 基于双种群交流的粒子群算法

标准PSO算法在适应度函数存在多极值时很容易陷入局部最优，双种群交流的PSO算法针对这一缺陷进行改进。

双种群交流PSO将粒子初始化为两个种群，即swarm1与swarm2，二者更新时互不干扰，到目前为止找到的最优适应度值分别为 fpg1和 fpg2，令 fpg=max(fpg1，fpg2)，直到连续K次 fpg都不变，两个种群开始交流。

2.1 双种群交流步骤

2.1.1 确定（被）学习种群

以目前 fpg为标准，按照模拟退火算法公式，对swarm1有：

若 ps＜rand()，则被学习种群为swarm1；反之被学习种群为swarm2。其中T为退火温度。采用上述方法后，使得目前最大适应度相对较坏的种群也有可能成为被学习对象。

2.1.2 确定学习种群的学习概率

根据学习种群中每个粒子自身到目前为止搜索到的历史最优适应度值大小对粒子进行连续编号。由于历史最优适应度值越大，该粒子对其他粒子的吸引力越强，为防止局部最优，就越需要向外界学习从而对其位置进行变异，该粒子编号应该越大。第i个粒子的学习概率为 pdi=0.5×(numberi/N)5+0.1，其中numberi是学习种群中第i个粒子的编号，N为学习种群规模。

2.1.3 更新粒子的速度与位置

被学习种群按照标准PSO更新速度与位置。学习种群中每个粒子都要根据学习得来的信息以新方式更新速度和位置。

当 pdi＞rand()时，该粒子向被学习种群靠拢，所涉及的区域相对当前位置而言在被学习种群一侧。速度更新公式如下（以swarm1向swarm2学习为例，下同）：

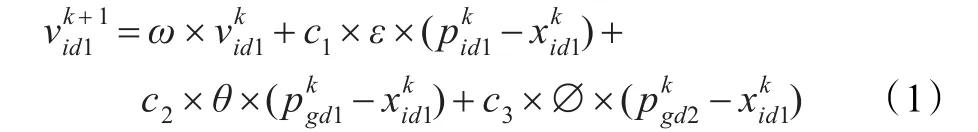
其中∅为[0，1]之间的随机变量。位置更新公式如下：

为了在学习中让粒子尽可能大步迈出当前的局部机制，突破速度范围的限制，引入速度约束因子γ，在更新位置时，起到调节速度的作用。γ的大小设置与速度的范围限制有关，设置原则是使该速度变异的粒子能够跳出当前的局部最优区域，尽可能向更大范围探索。如本文中速度的范围被设置为搜索空间范围的0.2倍，则γ设置为2.5，使得该粒子一次速度变异能够飞行的距离约为整个搜索空间的一半。经本文多次测试可知，当γ过小时，粒子很可能无法跳出当前局部极值区域，本次粒子学习失败；当γ过大时，往往会使粒子学习后的新位置溢出搜索空间边界，最终被重置于某一特定位置，这样很多粒子速度变异后都集中在被特设的区域，无法尽可能分散到整个搜索空间，会削弱整个种群的搜索能力。

当 pdi＜rand()时，该粒子向被学习种群背离，所涉及的区域相对当前位置而言在被学习种群一侧的相反方向。目的是覆盖整个搜索区域。速度更新公式如下：

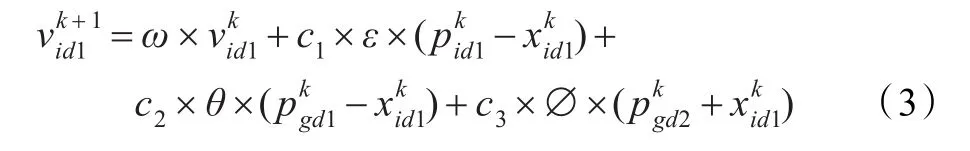
位置更新同公式（2）。

对于粒子位置的离散约束和范围约束采用惩罚函数的方法进行处理。

2.2 双种群交流流程图

双种群交流PSO算法流程图如图1所示。

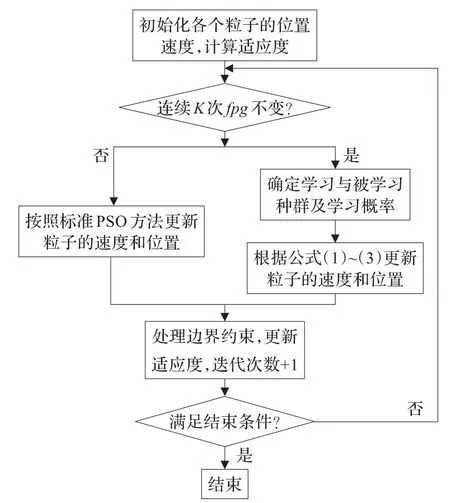
图1 双种群交流PSO流程图

3 符合我国实际情况的投资组合模型

3.1 投资组合约束函数

假设投资总额为total，投资比例向量为 x={x1，x2，…，xn}′，xi表示投资于每种风险资产的权重，σ表示每种风险资产收益率变化之间的协方差矩阵，即风险程度的衡量；Ri(i=1,2,…，n)表示第i种风险资产的预期收益率。

我国证券市场上存在以下几种限制因素：

（1）买空卖空限制：不允许买空与卖空，则0≤xi≤1。

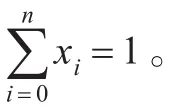
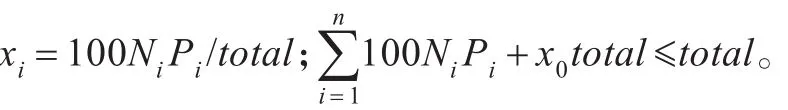
（4）交易费用：上证交易所买入股票的成本有：

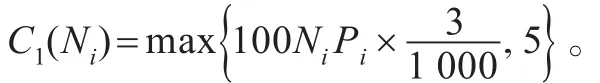
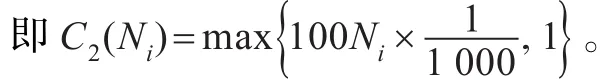
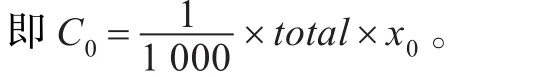
3.2 投资组合目标函数

在风险一定时，投资者会选择收益较大的组合；而在收益一定时投资者会选择风险较小的组合。其目标函数为：

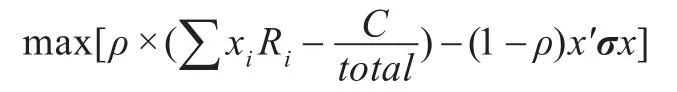
投资者可根据对风险的厌恶程度选择不同的系数ρ。

综上可得符合我国实际情况的投资组合模型为：

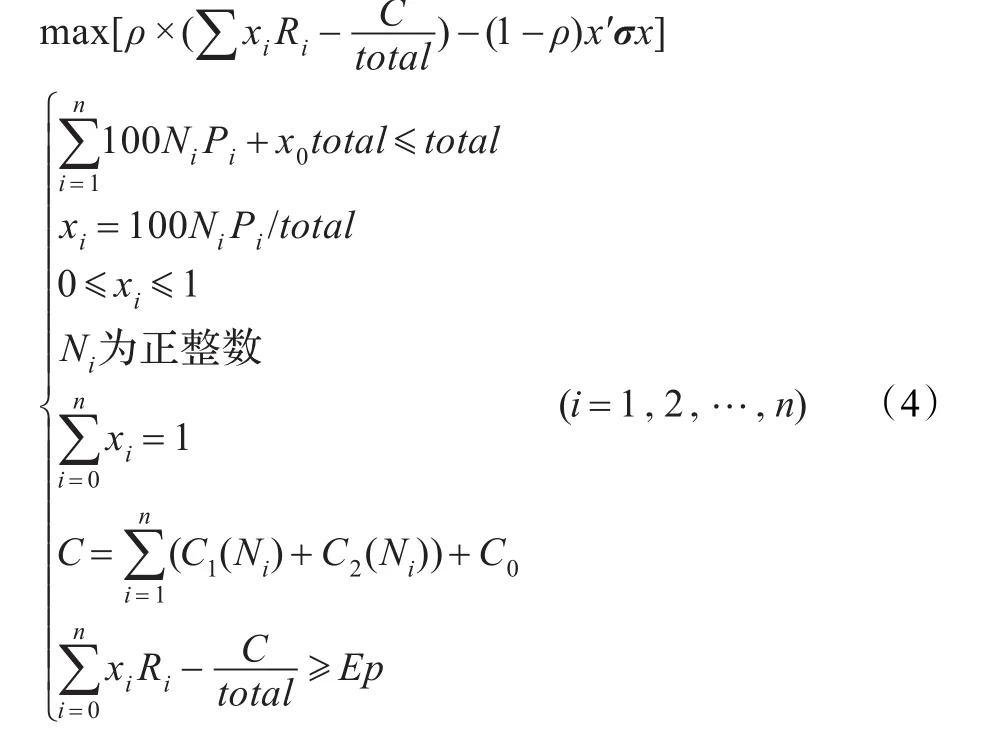
4 投资组合模型求解

4.1 样本与数据来源

由于2013年我国尚未发行一年期国债，所以使用三年期国债的年利率作为无风险收益率，为4.76%。本文所选股票全部来自上证A股，在农林牧渔、采矿业、建筑业、信息技术业、金融业、住宿和餐饮、水电煤、房地产、文化和社会工作、文化体育娱乐10个行业中选取了50支股票，利用2010、2011、2012全年收益率和2013第一季度收益率作为处理股票预期收益率的依据，并据其计算每只股票之间的协方差以衡量风险，实证所需要的股票价格和收益率等数据全部来自于“东北证券网上交易V6”平台。50只股票的基本情况如表1所示。

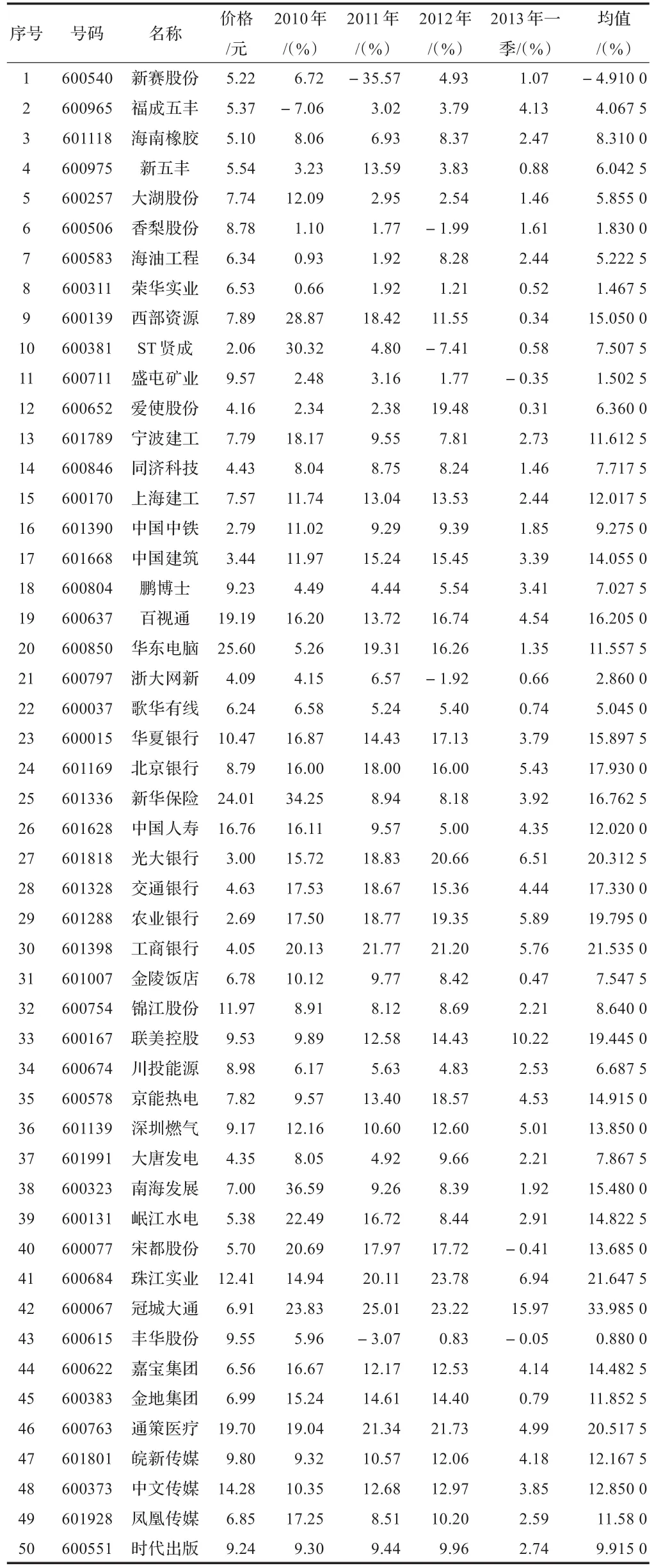
表1 上证交易所50支股票部分近年收益数据

表2 最优投资组合（期望收益率为8%时）1）

表3 最优投资组合（期望收益率为9%时）1）

表4 最优投资组合（期望收益率为10%时）1）

表5 最优投资组合（期望收益率为11%时）1）

表6 最优投资组合（期望收益率为12%时）1）

4.2 结果与分析

将50只样本全部引入模型，由投资者预期收益率、手数为整数、投资组合公式等作为约束条件，自由选择股票，并给出所投资的手数、组合的期望与标准差。初始投资额total为100万元。使用MATLAB编程所得最优投资组合如表2～表6所示。

由上述结果可以看出：

（1）随着投资者的期望收益率不断增加，标准差也不断增加，这符合风险收益正相关原理。

（2）在该模型中投资者可以根据自己对市场的预期改变其期望收益率，获得不同的投资组合。

（3）投资组合中，影响不同行业不同股票的非系统性风险不同，可能相互抵消，只需选择若干只收益率相关系数较小的股票进行投资即可，尽可能多地选择股票进行投资是没有意义的，因此该模型能对股票数目和种类进行自主选择。

（4）该模型能够按照我国股票市场上整数手数投资、买空卖空限制、交易费用限制、投资总金额有限等多种实际情况，有效指导投资者进行投资。

5 结束语

将改进的双种群交流离散PSO算法应用到我国股票市场上，不仅能够指导投资者选择股票种类进行组合，更能给出投资的比例，是一种切实可行的指导投资者构造资产组合的方法。

[1]Markowitz H W.Portfolio selection[J].Journal of Finance，1952，7（1）：77-91.

[2]辛沂.Hopfiel神经网络的稳定性及其在投资组合理论中的应用[D].济南：山东大学，2008.

[3]牛雪丽.差分进化算法及其在金融产品组合优化中的应用[D].济南：山东师范大学，2009.

[4]陈国华，廖小莲，余星.基于直觉模糊规划的多目标投资组合选择模型[J].模糊系统与数学，2012，26（2）：129-135.

[5]张长胜，孙吉贵，欧阳丹彤.一种自适应离散粒子群算法及其应用研究[J].电子学报，2011，37（2）：299-304.

[6]于颖，李永生，於孝春.粒子群算法在工程优化设计中的应用[J].机械工程学报，2008，44（12）：226-231.

[7]赵学奇.模拟退火改进的粒子群算法的研究及应用[D].武汉：华中科技大学，2012.

[8]黄太安，生佳根，徐红洋，等.一种改进的简化粒子群算法[J].计算机仿真，2013，30（2）：327-335.

[9]Wang X L.A model for portfolio selection based on particle swarm optimization with escape velocity[C]//International Conference on E-Business and E-Government，2010：3513-3516.

[10]陈炳瑞，冯夏庭.压缩搜索空间与速度范围粒子群优化算法[J].东北大学学报，2005，26（5）：488-491.

[11]刘冬华，甘若迅，樊锁海，等.基于捕食策略的粒子群算法求解投资组合问题[J].计算机工程与应用，2013，49（6）：253-256.

[12]何光，吴萌.基于改进粒子群算法的投资组合模型[J].计算机仿真，2013，30（2）：209-212.

[13]秦全德.粒子群算法研究及应用[D].广州：华南理工大学，2011.

WANG Xiuli,LIU Yang

School of Information,Central University of Finance and Economics,Beijing 100081,China

Considering that standard Particle Swarm Optimization（PSO）has the severe problem of being stuck in local optimums,this paper puts forward an improved particle swarm optimization with two particle swarms communicating with each other on the basis of velocity mutation,leading to the problem above to be resolved.In addition,taking into account the existence of transaction cost and the restraints of long sale,short sale,integral number of transactions and so on in China, this paper builds a portfolio selection model which totally reflects current status in our country.It applies the improved PSO above to deal with the model.The result comes out that the model is integrated and effective in our country,and also the PSO with two particle swarms communicating with each other is proper and efficient.

two particle swarms communicating with each other;Particle Swarm Optimization（PSO）;portfolio selection model

针对标准粒子群算法易陷入局部最优的缺陷，提出一种双种群交流的新型粒子群算法，利用速度变异成功地解决了上述问题；综合考虑了我国股票市场上的交易费用、整数手数投资、不允许买空卖空等问题，建立了符合我国股票市场的投资组合模型，并将双种群交流的离散粒子群算法应用于其求解过程中，给出最优投资组合。

双种群交流；粒子群优化；投资组合模型

A

TP399；F830.59

10.3778/j.issn.1002-8331.1308-0207

WANG Xiuli,LIU Yang.Discrete portfolio selection model based on particle swarm optimization algorithm with two particle swarms communicating with each other.Computer Engineering and Applications,2014,50（24）：227-230.

国家自然科学基金（No.61272398）；国家社会科学基金重点项目（No.13AXW010）；中央财经大学学科建设基金项目。

王秀利（1977—），男，博士，副教授，CCF高级会员，研究领域为信息经济、优化理论及应用。E-mail：xlwang.cufe@gmail.com

2013-08-15

2013-09-30

1002-8331（2014）24-0227-04

CNKI网络优先出版：2014-07-11，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1308-0207.html