基于LS算法的OFDM信道估计的研究与改进

王炼红，刘庆娜，刘宏力，罗 晶，张红俊

湖南大学 电气与信息工程学院，长沙 410082

基于LS算法的OFDM信道估计的研究与改进

王炼红，刘庆娜，刘宏力，罗 晶，张红俊

湖南大学 电气与信息工程学院，长沙 410082

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是一种多载波调制技术，它能够降低符号间干扰（ISI）和码间干扰（ICI）对信号的影响，而且频谱利用率高，能够有效地对抗多径时延扩展，因此OFDM成为新一代移动通信的关键技术之一[1-3]。MIMO技术在原有传输带宽和功率消耗的基础上，能成倍地提高频谱利用率，将MIMO技术和OFDM技术相结合能显著提高网络覆盖范围和传输可靠性[4-5]。而准确的信道估计是保证OFDM系统传输质量，发挥其优越性的关键所在。

MIMO-OFDM的最小平方（Least Square，LS）信道估计算法就是在发送端把已知的导频符号插入到OFDM符号的特定子载波上，经过信道后，在接收端提取这些特定位置的导频，并用LS算法估计出导频位置的信道响应，再做内插，通过导频位置的信道信息得到整个信道的信道响应。常见的插值算法有多种，文献[6]中通过仿真对比指出三次样条插值（spine）的性能最好，所以本文中采用三次样条插值。

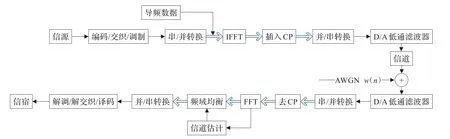
图1MIMO-OFDM系统结构图

LS估计算法由于在估计时忽略了噪声的因素，所以信道估计值对噪声干扰以及ICI的影响比较敏感，在信道噪声较大时，信道估计的准确性大大下降。文献[7]中提出通过加低通滤波器来降低噪声的影响，文献[8]中提出通过加窗来降低噪声影响。但是它们却不能消除通带内因突发传输引起的毛峰和尖刺。本文提出的切比雪夫FIR滤波器能很好地解决这些问题，而且较之传统的滤波器有良好的性能。

1 MIMO-OFDM的系统模型及LS算法

1.1 MIMO-OFDM的系统模型

基于导频信道估计的MIMO-OFDM系统的基带系统模型如图1所示。

发送端的二进制数据通过卷积编码、交织和调制映射，将二进制序列组映射到星座图中对应的点。然后进行串并转换，设OFDM的子载波数为Ns，将二进制信息进行分组，再以固定周期在所有子载波上加入导频或者在每个OFDM符号上的某些子载波上均匀插入导频，通过IFFT将长为Ns的频谱表达式{X(k)}变换成时域信号(x(n))，然后插入长度为Ng的循环前缀CP，引入保护间隔能有效地对抗多径时延带来的ISI。那么第m个子载波上的发送数据可表示为[9]：

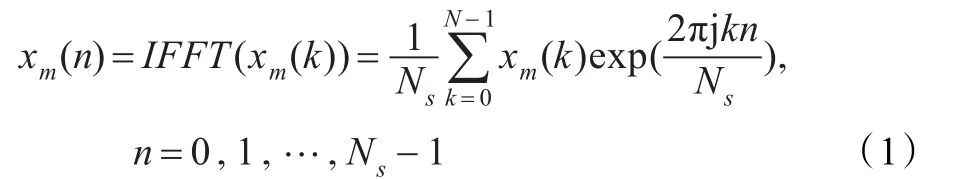
加入循环前缀后的时域发送信号 xm，g(n)可以表示为：

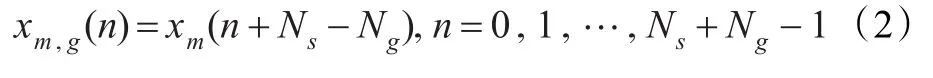
发送信号通过瑞利信道以及加性高斯白噪声（AWGN）的干扰后，到接收端的数据为：

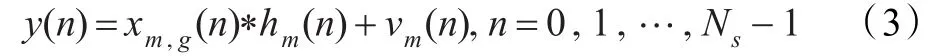
其中hm(n)表示第m个OFDM符号传输时信道冲激响应，vm(n)为加性高斯白噪声。接收信号经FFT变换到频域为：

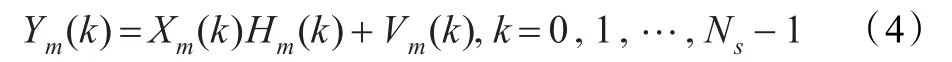
因此，信道估计的目的就是用Ym和已知发送的导频序列X估计出：

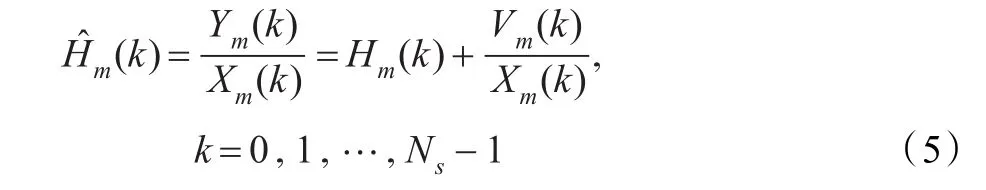
1.2 导频的选择

导频图案的选择是基于导频信道估计的OFDM系统设计的重要参数，它直接影响到信道估计结果的精确性和系统的最大数据传输速率。

常用的OFDM信道估计的导频插入方式有两种：块状导频和梳状导频，分别如图2、图3所示[11-12]。

图2 块状导频

图3 梳状导频

对于块状导频结构，连续多个OFDM符号构成一帧，在每一帧的第一个OFDM符号中，所有的子载波都发送导频，同一帧中的其他若干个OFDM符号发送信息。这样就可以利用导频OFDM符号来估计信道状态信息，同时将所估计的信道状态信息利用到后面信息OFDM符号的相干解调之中，直到下一个导频OFDM符号的出现。对于块状导频，由于导频出现在一个OFDM符号的所有子载波之中，因此它不需要在频域进行插值。块状导频受到多普勒频移的影响较大，只适用于慢衰落信道。

对于梳状导频，导频符号均匀分布在每个OFDM符号的某些固定位置的子载波上。在接收端先估计出导频符号位置上的信道状态信息，非导频符号位置上的状态信息是利用导频位置上的信道状态信息插值得到的。由于导频符号在时域上是连续的，因此它不需要考虑多普勒频移带来的影响。梳状导频图样适用于信道变化较快而多径时延相对较小的系统。基于本文仿真系统是快变信道，所以选用梳状导频结构。

1.3 LS信道估计算法

LS信道估计算法的代价函数为：

从上式中可以看到LS算法只需要知道发送信号，不需要其他的先验信息，因此LS估计算法的最大优点就是结构简单，计算复杂度小。

2 MIMO-OFDM信道估计LS算法的改进方法

LS信道估计算法由于在估计时忽略了噪声的因素，导致信道估计值对噪声干扰以及ICI的影响比较敏感，在信道噪声较大时，信道估计的准确性大大下降。所以本文设计了一种针对信道突发噪声的改进算法。

改进的重点是在加入突发噪声情况下，对切比雪夫滤波器的设计和应用。

本文提出的改进的LS算法思路是：首先给信号加入突发噪声，再让导频处估计出的信道冲激响应信号通过最优化滤波器，然后用插值算法得到整个信道的冲激响应。这样可减小LS算法的信道估计误差，从而提高整个系统的精度。其改进思路图如图4所示。

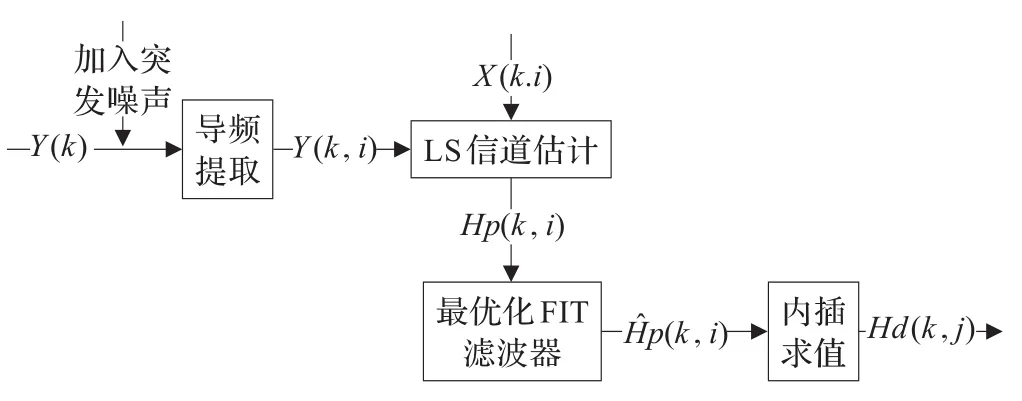
图4 LS算法的改进

2.1 切比雪夫滤波器的设计和引入

最优化设计的前提是最优准则的确定。在FIR滤波器最优化设计中，常用的准则有均方误差最小化准则和最大误差最小化准则，本文中用到的准则为最大误差最小化准则，也叫切比雪夫最佳一致逼近准则，表示为：

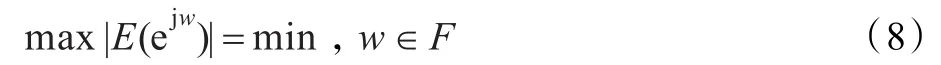
式中，F是根据要求预先给定的一个频率取值范围，可以是通带或阻带。

切比雪夫最佳一致逼近即先选择N个频域采样值，在给定频带范围内，使频率响应的最大逼近误差达到最小，也叫等波纹逼近，它可保证局部频率点的性能也是最优的，误差分布均匀，相同指标下，可用最少的阶数达到最佳化[13]。切比雪夫滤波器是在通带或者阻带上频率响应幅度等波纹波动的滤波器。在通带波动的为“I型切比雪夫滤波器”，在阻带波动的为“II型切比雪夫滤波器”。基于本文研究的是通带内有突发噪声的信道，所以采用“I型切比雪夫滤波器”，n阶第一类切比雪夫滤波器的幅度与频率的关系可用下列公式表示：其中：ε为限定的波纹系数，且|ε|＜1，w0为截止频率，=cos(n.arccos是n阶切比雪夫多项式[14]。

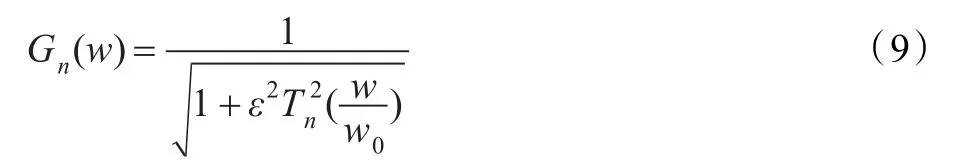
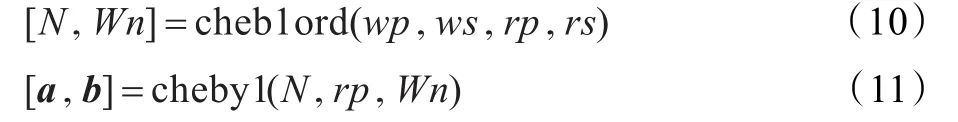
函数中的N表示滤波器的阶数；Wn表示截止频率；wp代表通带截止频率；ws代表阻带截止频率；rp、rs分别代表期望的通带波纹和阻带衰减，单位为dB，在设计滤波器时这两个是作为已知条件给出的；a、b分别表示设计的滤波器的分子和分母多项式系数向量。

关键要确定式（8）中F的取值范围，以确定切比雪夫带通滤波器的通带和阻带，最终设计出合理的切比雪夫滤波器。主要是在系统的LS信道估计模块（estimator_ ls.m）中进行滤波器函数的调用。

本文设计四个导频处的wp分别为[6.73E6，6.97E6]、[7.91E6，8.15E6]、[12.16E6，12.4E6]、[16.51E6，16.81E6]，ws分别为[5.69E6，7.01E6]、[7.87E6，8.19E6]、[12.12E6，12.44E6]、[16.47E6，16.85E6]，同时令rp=1，rs=25。 fs是信号的采样频率，设计 fs为40 MHz。

2.2 突发噪声的引入

无线通信网络中的差错主要是突发差错，突发差错大都是由冲激噪声引起的。冲激噪声幅度较大，持续时间要比数据传输中的每比特发送时间要长，因而冲激噪声会引起相邻多个数据位出错。突发噪声主要来自交换机和各种电器干扰、雷电干扰、电火花干扰、电力线感应等[15]，它的特点是：差错呈突发状，影响一批连续的bit（突发长度）。

传统的仿真系统中一般只使用高斯白噪声，但是单纯的高斯白噪声仿真环境不能满足实际情况中的需求，因为实际情况下，还会有突发噪声的存在。在数字通信中，它的影响是不容忽视的。一旦出现突发脉冲，由于它的幅度大，且无法靠提高信噪比来避免，将会导致一连串的误码，对通信造成严重的危害[16]。

上文中已经提出切比雪夫滤波器在过渡带衰减很快，且可以控制幅度的波动范围，所以在消除通带内因突发传输引起的毛峰和尖刺方面，比传统的加窗方法性能更优。本文的主要目的就是在仿真系统中加入突发噪声，然后对传统的加窗滤波器算法和本文提出的切比雪夫滤波器算法加以对比，以证明本文提出的算法的可靠性和有效性。

噪声的加入主要是在系统的信道模块（channel.m）。利用rand函数产生突发噪声，加入到发送信号中，使接收信号中既有高斯白噪声又有突发噪声。

3 改进的LS算法

本文采用的MIMO-OFDM系统参数为10 MHz的载波频率，基带系统带宽为20 MHz，基带抽样频率为40 MHz，子载波个数为64，循环前缀CP长度与有效FFT时间比例为1/4。对系统的863帧结构也进行了必要的简化，只考虑上行和下行时隙，不考虑切换时间，这样可以简化仿真过程。为便于仿真本文先定义一个用户单元，即进行一次仿真循环。

改进的LS算法实现步骤如下：

步骤1在信道参数产生部分，设置信噪比为Eb_ No_dB=[0∶2∶20]，产生不同用户、不同收发天线对、不同OFDM符号时间和多径信道不同时延径的时域信道响应，然后得到时域信道的参数。

步骤2在发射机部分，生成多用户数据和对信道进行编码。在此部分包括在数据符号帧之间插入导频OFDM符号，并在数据OFDM符号前加前导序列成帧。

步骤3多天线多径信道部分，在此部分对信号加入突发噪声，另外系统自带的高斯白噪声也在此加入。

步骤4接收机部分，这部分主要包括对OFDM符号解调，分离提取数据OFDM符号和导频OFDM符号，然后利用频域信道估计器对信道进行估计。本文的信道估计重点就在此处，就是在此模块对LS信道估计算法进行改进，加入最优化滤波器。

步骤5进行仿真性能分析，显示不同信噪比下的误码率（BER）和均方误差（MSE）曲线。

4 仿真结果与分析

采用MATLAB仿真软件，分别在未加突发噪声和加入突发噪声的情况下，对改进前的基本的LS信道估计算法、基于LS的传统加窗算法以及本文提出的基于LS的最优化滤波器算法进行了仿真比较。为了更好地达到仿真效果，系统选择了4发4收的MIMO-OFDM系统，仿真信道设定为最大多径时延为500 ns的室内无线信道，采用QPSK调制方式。改进前的基本的LS信道估计算法、基于LS的传统加窗算法以及本文提出的基于LS的最优化滤波器算法的BER性能比较曲线和MSE性能比较曲线分别如图5～8所示。

图5 未加入突发噪声时系统BER～（Eb/No）性能比较曲线

图5和图6是未加入突发噪声时，三种算法的性能比较曲线；图7和图8是加入突发噪声后，三种算法的性能比较曲线。通过性能比较曲线，可以看到，在有突发噪声的情况下，本文提出的基于LS的加最优化滤波器的改进算法比传统的加窗的LS算法效果好很多，其中从图6和图8显示的加突发噪声前和加突发噪声后信道估计方法的MSE性能仿真曲线可以看出，加入突发噪声后，改进的信道估计算法有效降低了信道估计的均方误差值。这是因为传统的加窗滤波器是一种数据先补零后加权的方法，不能有效提高频谱分辨力；而切比雪夫滤波器能实现先加权后补零，有利于减小数据的截断突变。

图6 未加入突发噪声时系统MSE～（Eb/No）性能比较曲线

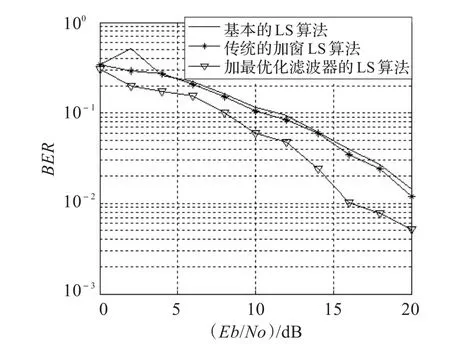
图7 加入突发噪声后系统BER～（Eb/No）性能比较曲线

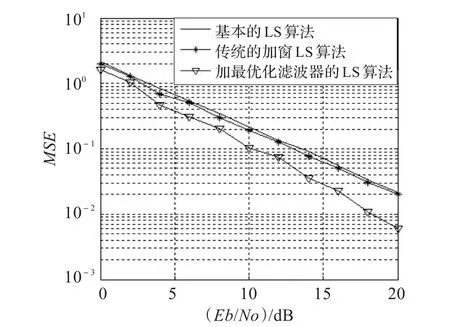
图8 加入突发噪声后系统MSE～（Eb/No）性能比较曲线

5 结束语

本文在研究MIMO-OFDM的信道估计的基础上，提出了一种基于LS的改进的信道估计算法。在有突发噪声的情况下，通过加入最优化滤波器，降低信息的误码率和均方误差。并通过仿真比较，验证了此算法的正确性和可行性，具有一定的实用价值，且此滤波器的设计也比较简单，容易实现。

[1]曾少华.LTE基础原理与关键技术[M].西安：西安电子科技大学出版社，2010：71-76.

[2]张继东，郑宝玉.基于导频的OFDM信道估计及其研究进展[J].通信学报，2003，24（11）：1-2.

[3]李瑾.MIMO-OFDM信道估计技术研究[D].长沙：中南大学，2009：8-13.

[4]石鑫，李昊.无线MIMO-OFDM通信系统原理及其关键技术[J].理论与方法，2010，29（2）：1-2.

[5]杨康.MIMO-OFDM系统关键技术的研究[D].西安：西安电子科技大学，2011：2-4.

[6]楚克丽.MIMO-OFDM信道估计技术研究与实现[D].成都：西南交通大学，2010：38-41.

[7]杨洪涛.基于导频的正交频分复用信道估计研究[D].北京：北京邮电大学，2010：49-53.

[8]刘冉，刘文进.MIMO-OFDM系统信道估计算法的改进[J].网络与通信，2010，8（3）：1-3.

[9]肖丽萍，郝磊，段再超.基于失配序列的OFDM信道估计[J].信号处理，2010，26（4）：2-3.

[10]周键，唐友喜，刘皓.叠加训练序列OFDM系统的一种迭代信道估计方法[J].电子学报，2007，35（z1）.

[11]刘海员，孙建成.基于导频的OFDM信道估计小波核SVM算法[J].系统工程与电子技术，2007，29（8）.

[12]张佳杰.基于导频的MIMO-OFDM信道估计技术研究[D].天津：天津大学，2009：22-25.

[13]李益华.MATLAB辅助现代工程数字信号处理[M].2版.西安：西安电子科技大学出版社，2010：122-126.

[14]吴小役，李长红，靳小军，等.切比雪夫滤波器在PMSM伺服系统中的应用[J].电力电子技术，2006，40（1）.

[15]王勇，葛建华，付少忠.脉冲噪声下的高可靠性OFDM信道估计[J].吉林大学学报，2007，37（6）：1-4.

[16]尹中秋，石春和，陈明生.基带通信中常见噪声的产生方法研究[J].传感器与仪器仪表，2006（31）.

WANG Lianhong,LIU Qingna,LIU Hongli,LUO Jing,ZHANG Hongjun

School of Electrical and Information Engineering,Hunan University,Changsha 410082,China

LS algorithm has been widely used in the OFDM channel estimation because of its simple operation.In actual systems,however,the algorithm is influenced by the noise of Inter-Carrier Interference（ICI）due to the presence of non-ideal factors.Meanwhile channel response will be interfered with outside noise in the burst transmission,which makes the estimated channel response amplitude fluctuate a certain range and have spikes and glitches.In order to solve this problem,an OFDM channel estimation based on the optimization of the FIR filter（Chebyshev filter）algorithms is proposed. Chebyshev filter attenuates quickly in the transition zone,and the error between it and the ideal filer frequency response curve is the smallest.So this algorithm can guarantee the performances of the local frequency are optimal compared to the traditional filer algorithm by simulation.The unexpected noise is introduced in the white Gaussian channel environment and a simulation of the proposed scheme is given.The simulation results show that this method can effectively eliminate the spikes and glitches in the passband caused by burst transmission.

Orthogonal Frequency Division Multiplexing（OFDM）;channel estimation;Least Square（LS）algorithm; Finite Impulse Response（FIR）filter;Mean Squared Error（MSE）

OFDM信道估计中，LS算法因其运算简单，得到了广泛应用。但是在实际的系统中，由于有非理想因素的存在，使得该算法受到载波间干扰（ICI）噪声的影响；并且突发传输时，信道响应会受到外界噪声的干扰，使估计的信道响应幅值在一定范围内上下波动，并带有尖峰和毛刺。为了解决此问题，提出了一种基于LS算法的最优化FIR滤波器（切比雪夫滤波器）信道估计算法。切比雪夫滤波器在过渡带衰减很快，和理想滤波器的频率响应曲线之间的误差最小，因此该算法较之传统的加窗算法，能保证局部频率点的性能也是最优的，进而有效地减小均方误差（MSE）。在高斯白信道环境下引入突发噪声，对所提方案进行了仿真，其结果验证了该方法能有效消除通带内因突发传输引起的毛峰和尖刺。

正交频分复用（OFDM）；信道估计；最小平方（LS）算法；有限长单位冲激响应（FIR）滤波器；均方误差（MSE）

A

TN925.5

10.3778/j.issn.1002-8331.1302-0005

WANG Lianhong,LIU Qingna,LIU Hongli,et al.Research and improvement of OFDM channel estimation based on LS algorithm.Computer Engineering and Applications,2014,50（24）：213-217.

国家自然科学基金（No.611720889）。

王炼红（1971—），女，副教授，硕士生导师，研究领域为通信领域和神经网络等；刘庆娜（1989—），通讯作者，女，硕士研究生，研究领域为通信领域。

2013-02-01

2013-03-22

1002-8331（2014）24-0213-05

CNKI网络优先出版：2013-04-10，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130410.1554.004.html