模糊时间窗VRP的动态规划和禁忌搜索混合算法
王君
天津财经大学 商学院,天津 300222
模糊时间窗VRP的动态规划和禁忌搜索混合算法
王君
天津财经大学 商学院,天津 300222
1 引言
带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows,VRPTW)应用到现实中时,顾客往往是给出一个比他们实际需要更窄的时间窗,实际配送服务中对时间窗的一点点违反对于顾客来说是可以接受的。有时在满足所有时间窗的情况下不一定能找到可行解,所以对时间窗约束的放松不仅能提高实施车辆调度计划的成功率,而且可以降低车辆配送的成本。虽然传统的软时间窗VRP能在一定程度上处理该问题,然而该方法仅仅是对违反时间窗时间的简单求和,没有考虑顾客对时间窗的主观偏好。鉴于此种情况,Tang等[1]提出了模糊时间窗(Fuzzy Time Windows)的概念,给出了管理配送服务水平的一个新思路。
应用顾客的偏好水平描述时间窗最早由Cheng等[2]通过对模糊预约时间(Fuzzy Due-Time)的定义提出。作者假定顾客的需求是希望在一个特定的时点得到服务,服务时间离该时点越远,顾客的满意度越低。在确定完车辆的行驶路径后,还需要对车辆到达顾客点后的开始服务时间进行决策,以提高顾客的总体满意水平。Tang等[1]采用顺序优化的方法来求解模糊时间窗VRP(VRP with Fuzzy Time Windows,VRPFTW),第一阶段求解常规VRPTW,最小化车辆行驶距离的目标,第二阶段对具有线性分段函数和二次凹函数形式的隶属度函数,分别用割平面法或者次梯度投影算法计算顾客的最优开始服务时间,提高顾客的满意度目标。Ibaraki等[3]研究了软时间VRP,应用局部邻域搜索确定路径规划,并设违反时间窗约束的惩罚函数为线性分段凹函数的形式,应用动态规划方法和二叉搜索树的存储结构计算顾客的最优开始服务时间。VRPFTW需要考虑车辆配送成本、顾客偏好程度、车辆载重限制约束等,所以VRPFTW同样也是多目标最优化问题[4],需要采用多目标优化方法进行求解。
采用Pareto技术的智能算法是求解多目标VRP的一种有效方法,如多目标遗传算法[5-7]、多目标粒子群算法[8]、多目标蚁群算法[9-10]、多目标禁忌搜索算法(Multi-Objective Tabu Search,MOTS)[11-13]等。借鉴以上思路,本文提出一种求解VRPFTW的MOTS集成优化方法,应用了Pareto最优方法权衡多个目标的同时最优化。为了在MOTS算法中优化顾客的平均满意度目标,进一步在可行路径规划上提出了求最优开始服务时间的动态规划方法,利用阶段划分思想把问题化为基于紧路径的一维优化子问题。对于模糊时间窗为线性分段形式的隶属度函数,给出一种有限枚举算法,对于非线性的凹隶属度函数,给出一种次梯度二分迭代算法。最后通过Solomon的标准算例不仅验证了基于动态规划方法求最优服务时间的有效性,而且与目前主流的NSGA-II算法的比较实验,进一步说明了MOTS求解VRPFTW问题的优势。
2 问题描述与数学模型的建立
2.1 模糊时间窗的描述
顾客i的模糊时间窗包含可以容忍的时间范围[EETi,ELTi]和期望服务时间范围[Ei,Li],如图1所示。如果顾客i在期望服务时间范围[Ei,Li]内得到服务,顾客会得到最大的满意度(μi=1,μi表示顾客i的满意度,0≤μi≤1);如果顾客在容忍时间范围[EETi,ELTi]外得到服务,顾客不满意(μi=0);如果顾客的开始服务时间落在两个范围之间,那么顾客的满意度会随着与区间[Ei,Li]距离的增大而逐渐降低。模糊时间窗反映了顾客对时间的偏好程度,可以表示为关于时间ti的凹模糊数,ti表示车辆开始服务顾客i的时间,顾客的满意度可以用隶属度函数μi(ti)来表示。在实际问题中,为了建立良好的客户关系,一般会要求对顾客的服务水平至少要达到最低满意度λi,此时对应一个可行的时间范围[E^i,L^i],即车辆必须在该时间范围内开始对顾客进行服务。

图1 模糊时间窗示意图
定义1(λ水平时间窗)使顾客对开始服务时间的偏好水平不低于λ的时间范围,称为λ水平时间窗。
2.2 模糊时间窗VRP数学模型的建立
一个VRPFTW描述为:设G={I,E}为一个完备的无向图,其中 I={0,1,…,n}为节点集,E={i,j},其中i,j∈I,i≠j为边集。0代表车库点,其余为顾客点,一队具有有限装载能力的车辆从车库点出发,实现对所有顾客点的配送服务,最终回到车库。每个顾客点有固定的需求、固定的服务时间和模糊时间窗,并且只能由一辆车服务。优化目标是确定车辆的行驶路线,使得总费用最小,车队服务满意度最高。
标号和参数变量:
cij表示i点和 j点间的距离;V表示车辆集合;tij,ati,wti,sti分别表示车辆从节点i到 j的行驶时间、到达节点i的时间、在服务节点i前的等待时间和服务点i的持续服务时间;di表示第i个顾客的配送货物量;Qv表示车辆v的载重量。
决策变量:
xijv是0-1的决策变量,即

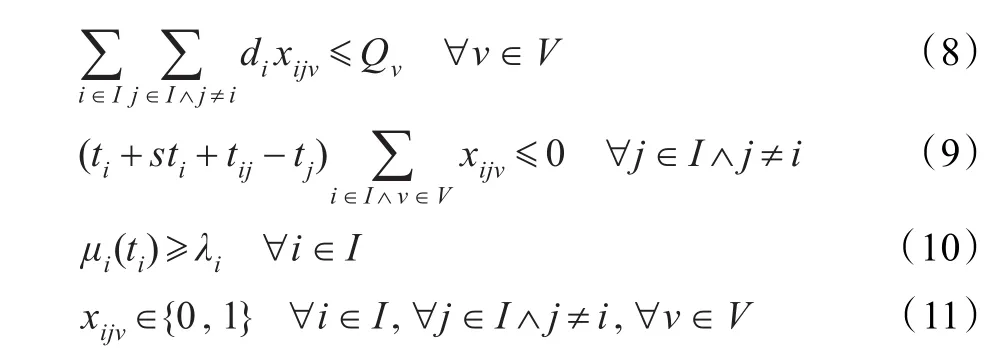
其中,式(2)和(3)表示目标函数,两个目标分别指最小化车辆行驶总路径长度和最大化顾客平均满意度。式(4)和(5)表示每辆车都要从车库出发,最终回到车库。式(6)和(7)表示每个顾客有且仅有一辆车为其服务。式(8)表示要货量不能超过车辆的载重量。式(9)表示车辆服务相邻顾客的时间关系。式(10)表示至少要达到顾客的最低满意度λi。式(11)指决策变量xijv是0-1变量。
3 多目标集成优化求解方法
VRPFTW需要同时优化车辆行驶总距离和顾客的平均满意度,本文依据解的Pareto占优关系来比较解的优劣以指导搜索方向,提出一种求解VRPFTW的基于并行多目标禁忌搜索的集成优化方法。算法首先应用随机车辆配载方法生成初始解并存储在一个候选解池中,然后对池中的Pareto解进行独立的禁忌搜索。初始解和邻域操作得到的候选解需要通过动态规划的方法来计算顾客的最优开始服务时间以优化平均满意度,并通过Pareto占优关系更新候选解池中的劣解,最终逼近Pareto前沿。
集成优化方法主要是把计算最优开始服务时间的动态规划方法集成到多目标禁忌搜索算法中。在MOTS算法本身的流程执行过程中,实际上是以λ水平时间窗替代传统时间窗,然后求解VRPTW问题。而每当MOTS中生成一个可行解,就要对该可行解进一步优化每个顾客的开始服务时间。图2给出的例子描绘了一个车的配送计划,上方时间轴表示采用MOTS本身流程优化的一个车辆的路径计划,是把λ水平时间窗看做传统时间窗,采用初始解生成方法和邻域结构得到的解。下方的时间轴是根据上方时间轴的路径计划,用动态规划方法对每个顾客的开始服务时间进行优化后的结果。优化直接提高了一部分顾客的满意度,从而提高了总体的满意度水平。
3.1 初始解与可行邻域结构
初始解决定了算法搜索的起始点,质量优的初始解能使算法快速收敛到最优解。首先以λ水平时间窗作为计算依据,采用随机车辆配载方法[14]生成PN个初始解,以保证每个初始解都满足约束条件。
邻域结构的选择对算法的搜索质量和效率影响较大,因为VRPFTW不仅需要考虑车辆的载重量约束,还要考虑模糊时间窗以满足顾客的最低满意度水平。如果在邻域搜索过程中不考虑λ水平时间窗,会产生大量的不可行解,即存在顾客i使得 μi(ti)<λi。为了提高算法性能,本文提出一种λ可行邻域结构,保证可行解通过邻域的作用生成的解仍然是可行的,即满足载重量约束和λ水平时间窗约束。
定义2(λ可行邻域结构)任意一个满足载重量约束和λ水平时间窗约束的路径计划,经过邻域结构的作用后,生成的新路径计划仍然满足载重量约束和λ水平时间窗约束,则称该邻域结构为λ可行邻域结构。根据不同的邻域操作,可以定义不同的λ可行邻域结构。
定义3(插入λ可行邻域)由插入操作作用的λ可行邻域结构称为插入λ可行邻域。对于一个可行的单车辆路径,判断一个顾客插入到该路径的各个位置是否满足载重量约束和λ水平时间窗约束,如果满足,则将该顾客插入到可行位置。
定义4(2-Optλ可行邻域)由2-Opt操作作用的λ可行邻域结构称为2-Optλ可行邻域。2-Optλ可行邻域是将两条单车辆路径从中间断开再交叉组合生成两个新的路径,或是把两个路径尾首相接,由一辆车单独进行配送服务。
3.2 动态规划方法计算最优开始服务时间
通过随机车辆配载方法生成的初始解和λ可行邻域结构生成的候选解,每个顾客的开始服务时间都是其最早的可以开始服务的时间。为了让候选解得到最大的服务满意度,在不改变路径计划的前提下,需要对每个顾客的开始服务时间进行调整。对某车辆配送的路径(s1,s2,…,sp,…,sP),sp∈I,根据文献[14]的紧路径定义,下面以紧路径优化子问题为计算单元,给出计算最优开始服务时间的动态规划方法。

图2 计算顾客最优开始服务时间的示意图
对于每辆车给定的路径计划,可以按照服务的顺序对P个顾客划分成P个阶段,每个阶段需要对相应顾客的开始服务时间进行决策。对当前顾客的决策会影响相邻的顾客,当每个顾客的开始服务时间确定以后,就组成了一个决策序列。显然,最优服务时间的确定是一种多阶段最优决策问题,而动态规划正是解决多阶段最优决策问题的有效方法。
阶段划分:如前所述,根据车辆对顾客的服务顺序划分P个顾客为P个阶段,p为阶段变量,p=1,2,…,P。
状态变量:车辆到达顾客点sp的时间atsp为状态变量,这里状态变量是连续的。
决策变量:车辆开始服务顾客点sp的时间tsp为决策变量,允许决策集合为max{,atsp}≤tsp≤L^sp。
状态转移方程:确定阶段 p的决策变量tsp之后,车辆对顾客sp进行服务,然后行驶一段路程后才能到达下一个顾客sp+1,故状态转移方程为atsp+1=(tsp+stsp+tspsp+1)。



一个状态为atsp阶段 p的优化问题,可以转化为下面的阶段优化问题:

次梯度投影方法要求对每次递推的自变量求其在可行域上的欧式投影,这本身又是一个多维优化问题。为了能够简化该方法,应用动态规划方法可以逐步对紧路径进行优化,从而把多维优化问题转化为一维优化问题,降低处理问题的难度。


即转化为一维的约束优化问题,其中μ⌒(·)是一个分段的凹函数。
(1)如果隶属度函数μ(·)是线性的,则μ⌒(·)是一个分段的线性函数,紧路径优化问题可以用有限枚举算法来优化。
(2)如果隶属度函数μ(·)是非线性的,则μ⌒(·)是一个分段的凹函数,本文提出次梯度二分迭代方法求解紧路径优化问题。
次梯度:


步骤2确定由sp开始的最长紧路径(sp,sp+1,…,sq)。若q=P并且wtsq+1=0,阶段优化完毕;否则,继续步骤3。
步骤3优化紧路径(sp,sp+1,…,sq),若优化后wtsq+1>0,阶段优化完毕;否则,返回步骤2。
3.3 MOTS总体流程

图3 MOTS流程示意图
MOTS的总体流程如图3所示,解的评价方法、适应度函数、禁忌对象、禁忌表、特赦准则、停止规则和长期表的设置与文献[14]相同。MOTS采用一个候选解池的存储结构和Pareto排序机制实现对全局搜索的控制。虚线所框部分描述了每个独立的搜索过程,每个搜索有独立的禁忌表和一个Pareto候选解列表,以记录其找到的局部Pareto解。在生成初始解和用邻域结构产生候选解之后,已经确定了目标 f1,需要进一步计算顾客的最优开始服务时间来优化目标 f2,所以MOTS算法中嵌入了3.2节提出的动态规划方法以综合评价解的优劣。
4 仿真实验与讨论
测试采用国际上通用Solomon的标准算例rc101,该算例包含100个顾客,顾客在地理位置或者服务时间窗上部分具有聚集特征,部分为随机生成。rc101的整个计划时间窗较短,每条线路中只能安排几个顾客。算法用VC++6.0进行编程,在Inter Pentium Dual T2410 CPU 2 GHz,1 GB内存,Windows XP SP3的主机上运行。实验主要包括两部分,首先比较本文提出的计算最优开始服务时间的动态规划方法和文献[1]提出的次梯度投影方法(记为PSM)的优劣,然后对本文提出的MOTS集成算法和目前比较主流的成熟多目标求解算法NSGA-II进行对比分析。
4.1 模糊时间窗的实验设定


4.2 计算最优开始服务时间方法的对比
用随机车辆配载方法分别对模糊时间窗的两类隶属度函数分别生成800个可行解,然后对每个可行解分别应用次梯度投影方法和基于动态规划的方法(记为DP)来计算最优开始服务时间。参数设置为:η=0.001,PSM方法如果在迭代过程中得到最大满意度1,则停止,且最大迭代次数设定为100。
表1的左半部分统计了PSM和DP的平均运算时间,Mean time是指计算每个解的最优开始服务时间所消耗的计算机平均运行时间;右半部分给出了在SPSS软件中做Wilcoxon signed ranks检验的统计分析结果,根据Z值可以判定两种方法在统计意义上存在显著性差异。对于线性的隶属度函数,DP方法的计算结果要明显优于PSM,并且计算时间还缩短了18.038%;而对于非线性的隶属度函数,DP方法计算结果的优势虽然不明显,但是计算时间缩短了74.150%。因为虽然从直观来看,阶段的划分使DP方法需要大量的计算子单元,但是其每个计算单元相比PSM要简单许多。PSM的逐步迭代和渐进寻优的策略,其收敛速度受步长的限制,而次梯度二分迭代算法能更快地收敛到最优解。由对比结果可以肯定,本文提出的DP方法要显著优于PSM。

表1 PSM和DP的运算时间及Wilcoxon signed ranks检验(SPSS软件)
4.3 MOTS算法和NSGA-II算法的对比
为了证明本文提出MOTS集成算法的有效性,与目前比较主流的成熟多目标求解算法NSGA-II进行对比。NSGA-II对父代和子代的群体混合并采用基于Pareto排序和拥挤度的选择方式,这里采用父代个体两两配对进行交叉,交叉算子采用BCRC交叉算子[15],并结合插入λ可行邻域,变异算子采用2-Optλ可行邻域,变异概率0.2,种群数量400。MOTS算法参数设置如下:NMAX= 9,候选解数量=80,候选解池容量=800。MOTS达到最大迭代数1 000或者最优解在迭代200次不变,算法终止。
表2列出了MOTS和NSGA-II运行结果得到的Pareto解的个数和平均求得每个Pareto解的运行时间。数据表明MOTS不仅比NSGA-II取到更多的Pareto解,并且MOTS求解每个解消耗的时间明显低于NSGA-II,尤其在隶属度函数为非线性形式时缩短了62.853%,所以MOTS的优势很大。图4和图5分别显示了线性和非线性的隶属度函数下MOTS和NSGA-II最终求得的Pareto前沿,对比表明MOTS计算得到的Pareto解集明显优于NSGA-II。因为NSGA-II得到的Pareto解个数与种群规模相关,如果要得到更多的Pareto解,必须扩大种群规模。实验表明在占用相同存储空间的情况下,MOTS通过候选解的持续生成,既能扩大搜索区域,又能提高搜索的密度。

表2 NSGA-II和MOTS运行结果统计

图4 线性隶属度函数NSGA-II和MOTS计算结果对比图

图5 非线性隶属度函数NSGA-II和MOTS计算结果对比图
5 结束语
模糊时间窗VRP考虑了顾客对时间窗的偏好,相比传统硬时间窗VRP,虽然顾客的满意度有一点下降,但是在顾客容忍的范围内,会大大节约物流配送成本。本文提出的基于λ可行邻域结构的多目标集成优化方法,在MOTS中嵌入了优化顾客满意度的动态规划方法,运用阶段划分,把原问题分解为关于紧路径的优化子问题。对模糊时间窗为线性分段函数形式和非线性凹函数形式的隶属度函数,分别提出了有限枚举算法和次梯度二分迭代算法来优化顾客的最优开始服务时间。集成方法求得的一组Pareto解,能有效帮助决策者权衡不同的决策目标,做出正确的管理决策。对比仿真实验表明,基于动态规划的方法能有效优化模糊时间窗VRP的顾客满意度,MOTS集成算法对比NSGA-II方法在求解精度和计算速度上都具有明显的优势。
[1]Tang J F,Pan Z D,Fung R Y K,et al.Vehicle routing problem with fuzzy time windows[J].Fuzzy Sets and Systems,2009,160(5):683-695.
[2]Cheng R,Gen M,Tozawa T.Vehicle routing problem with fuzzy due-time using genetic algorithms[J].Japanese Journal of Fuzzy Theory and Systems,1995,7:665-679.
[3]Ibaraki T,Imahori S,Nonobe K,et al.An iterated local search algorithm for the vehicle routing problem with convex time penalty functions[J].Discrete Applied Mathematics,2008,156(11):2050-2069.
[4]Jozefowiez N,Semet F,Talbi E G.Multi-objective vehicle routing problems[J].European Journalof Operational Research,2008,189(2):293-309.
[5]Tan K C,Chew Y H,Lee L H.A hybrid multi-objective evolutionary algorithm for solving truck and trailer vehicle routing problems[J].European Journalof Operational Research,2006,172(3):855-885.
[6]Jozefowiez N,Semet F,Talbi E G.An evolutionary algorithm for the vehicle routing problem with route balancing[J].European Journal of Operational Research,2009,195(3):761-769.
[7]Jozefowiez N,Semet F,Talbi E G.Target aiming Pareto search and its application to the vehicle routing problem with route balancing[J].Journal of Heuristics,2007,13(5):455-469.
[8]赵燕伟,李川,张景玲,等.一种新的求解多目标随机需求车辆路径问题的算法[J].计算机集成制造系统,2012,18(3):523-530.
[9]李琳,刘士新,唐加福.B2C环境下带预约时间的车辆路径问题及多目标优化蚁群算法[J].控制理论与应用,2011,28(1):87-93.
[10]李世威,王建强,曾俊伟.求解VRPTW问题的多目标模糊偏好蚁群算法[J].计算机应用研究,2011,28(12):4495-4499.
[11]Choobineh F F,Mohebbi E,Khoo H.A multi-objective tabu search for a single-machine scheduling problem with sequence-dependent setup times[J].European Journal of Operational Research,2006,175(1):318-337.
[12]Belfares L,Klibi W,Lo N,et al.Multi-objectives Tabu search based algorithm for progressive resource allocation[J].European Journal of Operational Research,2007,177(3):1779-1799.
[13]Carcangiu S,Fanni A,Montisci A.Multiobjective tabu search algorithms for optimal design of electromagnetic devices[J].IEEE Transactions on Magnetics,2008,44(6):970-973.
[14]王君,李波.带模糊预约时间的车辆路径问题的多目标禁忌搜索算法[J].计算机集成制造系统,2011,17(4):858-866.
[15]Ombuki B,Ross B J,Hanshar F.Multi-objective genetic algorithms for vehicle routing problem with time windows[J].Applied Intelligence,2006,24(1):17-30.
WANG Jun
School of Business,Tianjin University of Finance&Economics,Tianjin 300222,China
The Vehicle Routing Problem with Fuzzy Time Windows is addressed.A multi-objective mathematical model is designed with the objectives of logistics cost and average customer satisfaction.Based on Pareto dominance theory,a multiobjective tabu search algorithm is proposed to solve multi-objective optimization problems.Moreover,a dynamic programming method is embedded in the algorithm to optimize the customer satisfaction,which simplifies the original problem into tight path optimization sub-problems with the use of phasing.While fuzzy time windows are in piecewise linear and nonlinear convex membership function forms,customer beginning service time is optimized by proposed limited iteration subgradient algorithm and median iteration subgradient algorithm,respectively.Computational experiments on Solomon’s benchmark not only verify that the dynamic programming is more effective than projected subgradient methods to optimize the service level,but also show the advantages of the proposed multi-objective tabu search approach when compared with the well-known NSGA-II method.
vehicle routing problem;fuzzy time windows;dynamic programming;multi-objective tabu search;Pareto optimization
为优化具有模糊时间窗的车辆路径问题,以物流配送成本和顾客平均满意度为目标,建立了多目标数学规划模型。基于Pareto占优的理论给出了求解多目标优化问题的并行多目标禁忌搜索算法,算法中嵌入同时优化顾客满意度的动态规划方法,运用阶段划分,把原问题分解为关于紧路径的优化子问题。对模糊时间窗为线性分段函数形式和非线性凹函数形式的隶属度函数,分别提出了次梯度有限迭代算法和次梯度中值迭代算法来优化顾客的最优开始服务时间。通过Solomon的标准算例,与次梯度投影算法的比较验证了动态规划方法优化服务水平的有效性,与主流的NSGA-II算法的对比实验表明了该研究提出的多目标禁忌搜索算法的优越性。
车辆路径问题;模糊时间窗;动态规划;多目标禁忌搜索;Pareto最优
A
TP29;N945.25
10.3778/j.issn.1002-8331.1303-0092
WANG Jun.Dynamic programming and tabu search hybrid algorithm for Vehicle Routing Problem with fuzzy time windows.Computer Engineering and Applications,2014,50(24):58-64.
国家社科基金资助项目(No.11CGL102);教育部人文社科青年项目(No.13YJC630195);天津市科技发展战略研究计划项目(No.13ZLZLZF04600);天津财经大学科研发展基金资助项目(No.Q1208)。
王君(1983—),男,博士,讲师,研究领域为物流工程,智能优化等。E-mail:woosuny@163.com
2013-03-08
2013-06-13
1002-8331(2014)24-0058-07
CNKI网络优先出版:2013-06-26,http∶//www.cnki.net/kcms/detail/11.2127.TP.20130626.1539.007.html
◎网络、通信、安全◎

