一种基于双通道DPCA的SAR-GMTI杂波抑制方法

王肖洋 高 贵 周石琳 邹焕新

(国防科学技术大学电子科学与工程学院 长沙 410073)

一种基于双通道DPCA的SAR-GMTI杂波抑制方法

王肖洋*高 贵 周石琳 邹焕新

(国防科学技术大学电子科学与工程学院 长沙 410073)

偏置相位中心天线技术(DPCA)作为空时自适应信号处理(STAP)技术的特殊形式，在合成孔径雷达地面动目标指示(SAR-GMTI)领域得到了广泛的应用。杂波抑制的能力直接决定了GMTI的性能，传统的复图像域DPCA技术对于地杂波抑制能力有限，特别是广泛分布着强散射静止地物的城市区域。该文利用干涉相位对DPCA幅度进行非线性加权，提出了一种加权DPCA杂波抑制方法，该方法降低了通道间残差相位对DPCA杂波抑制的影响。实验结果表明：该文方法在杂波抑制能力上优于传统DPCA方法。

空时自适应信号处理(STAP)；偏置相位中心天线(DPCA)；合成孔径雷达(SAR)；地面动目标检测(GMTI)；杂波抑制

1 引言

空时自适应信号处理(Space Time Adaptive Processing,STAP)早期主要用于机载预警雷达中抑制强度大且分布广的地杂波和海杂波。近年来随着技术不断进步，该方法的使用范围进一步拓展，已被引入到合成孔径雷达地面动目标检测(SAR-GMTI)领域中[1－3]。STAP已经与偏置相位中心天线(Displaced Phase Center Antenna,DPCA)技术、沿迹干涉(Along Track Interfermetric,ATI)技术一起成为多通道SAR地面动目标指示的三大主流技术。然而，由于其设备复杂、计算量大、工程实现困难[4,5]等缺点，目前在SAR-GMTI领域仅取得了有限的应用。取而代之的是，复图像域DPCA技术作为空时自适应信号处理的特殊形式，以其简单易于实现的优点已成为多通道SAR动目标指示领域的一种流行方法，并在实际SAR地面监视系统中得到验证，如加拿大防务中心在RADARSAT-2地面动目标指示试验中验证了双通道DPCA技术的有效性[6,7]。

值得注意的是，DPCA 技术在实际SAR-GMTI系统中的表现并不理想。传统复图像域DPCA方法是对双通道复数据进行了作差取模处理(通常称之为DPCA幅度)，在理想假设条件下，运动目标的差值模(即DPCA幅度)不为零，而静止地物的差值模为零，故而地杂波能被对消。事实上，DPCA幅度与两通道数据的相位差密切相关，而相位差恰好反映了地物的动静信息，但平台抖动、通道失配、随机噪声等引起的通道去相关使得两幅复图像中对应杂波像素之间存在残差相位，当杂波回波强度很强时，杂波的DPCA幅度可能达到一个显著的水平，对于地面强散射静止物体的抑制能力极为有限[8,9]。因此，如果能降低残差相位对杂波DPCA 幅度的影响，则可能提高DPCA方法对杂波的抑制能力。

为此，本文尝试对两通道干涉相位进行非线性变换，然后利用变换后的干涉相位对DPCA幅度进行加权，来降低残差相位对DPCA幅度的影响。理论分析和实际数据实验都验证了该方法的有效性。

2 DPCA基本原理

2.1 DPCA杂波抑制原理

在机载(星载)雷达中，DPCA方法通过在运动平台上沿航迹搭载两幅天线，天线的相位中心之间偏置一定距离，两幅天线的相位中心联合使用，使天线相位中心在相继的发射脉冲时间里相对于地面静止不动，这样采用两脉冲相消就可以抑制地面杂波[10,11]。其基本原理示意图如图1所示。

天线中心间距为d，雷达脉冲重复频率为PRF，平台速度为Va，箭头所指为平台飞行方向，通道1发射信号，通道1和通道2同时接收信号，接收第1个回波信号时，通道1的接收相位中心在O1点，通道2的接收相位中心在O点，如果满足条件：

2.2 复图像域DPCA杂波抑制原理

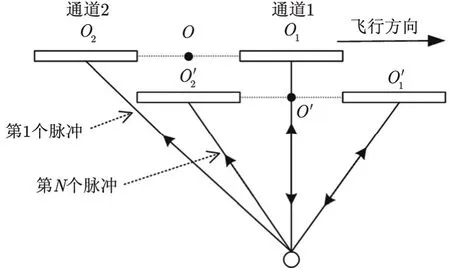
图1 DPCA原理示意图Fig. 1 DPCA schematic diagram

采用距离多普勒域DPCA方法进行动目标检测，必须满足式(1)，但在实际飞行过程中，平台会出现上下颠簸偏航现象，天线间距、平台速度和脉冲重复频率之间不再满足式(1)的关系，这就使得DPCA的杂波抑制效果很差。由于成像过程会对回波信号做平台运动补偿，并且信号经过聚焦处理后，运动目标信噪比较信号域有所提高，因此在复图像域进行DPCA检测将有可能使杂波抑制效果得到改善，复图像域DPCA杂波抑制原理图如图2所示。理想情况下，对于同一距离向分辨单元不同方位位置的地物，两通道接收的回波数据经过距离方位2维压缩成像后得到两幅1维复图像I1(t )和I2(t)，杂波对消特性如式(2)所示[11]：

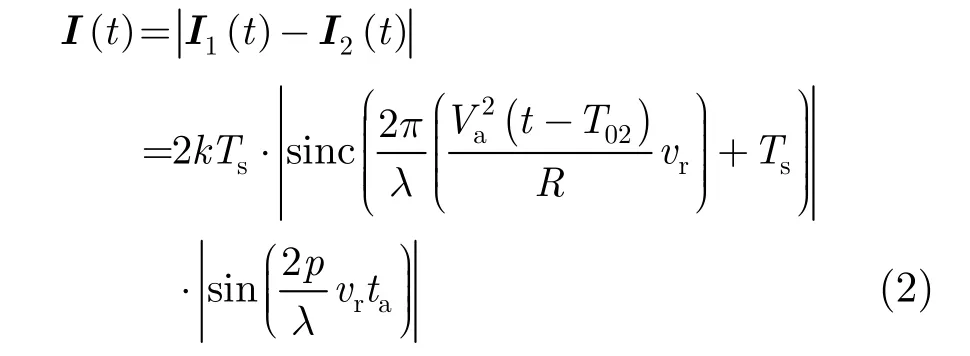
其中λ是波长，k是和目标后向散射系数有关的常数，vr为目标相对于平台的径向速度，T02与目标方位向坐标和平台飞行速度有关，Ts是合成孔径时间。当目标静止即vr=0时，I(t)=0，即静止杂波被消除。

2.3 复图像域DPCA杂波分布特性

由于通道失配、平台偏航、配准校准误差等多种因素的存在，将两通道复数据经过DPCA方法处理后，地杂波DPCA幅度并没有被绝对抑制为0，对于复杂的非均匀地物场景，假设目标缺失的前提下，地杂波分布近似服从自由度为(2n,2v)的尺度F分布，多视DPCA概率密度函数呈现为以下特性[7]：

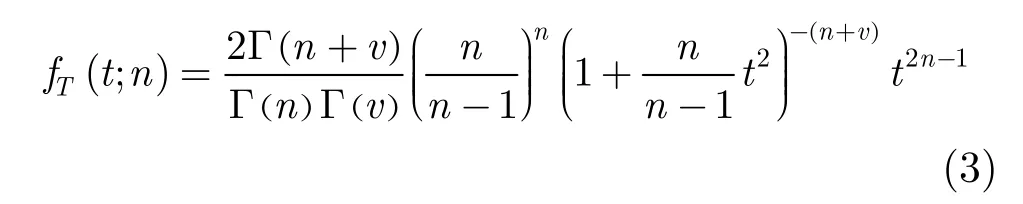
其中Γ(⋅)是伽马函数，n为视数，v为纹理参数，T为多视DPCA检测量，从图2可以看出杂波分布并没有集中在0附近，存在展宽拖尾现象，因此在保证较高检测概率的情况下，基于DPCA幅度的恒虚警检测常常有显著的虚警率。尤其是对于弱散射慢速运动目标，传统的DPCA检测方法很难将其与杂波分离开。

3 加权DPCA杂波抑制方法

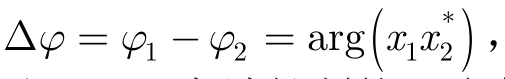
图中黑色实线表示像素x1的矢量图，蓝色实线表示像素x2的矢量图，绿色弧线代表两像素间的残差相位，红线代表DPCA幅度。图4(a)表示无系统噪声干扰，只存在通道不平衡；图4(b)和图4(c)表示通道增益相等，只存在系统噪声引起的去相关，图4(b)和图4(c)的区别在于像素(信号)幅度不同；图4(d)表示系统噪声和通道不平衡同时存在。

由图4(a)和图4(d)可以看出，通道不平衡时，即使是微小的残差相位也使杂波残留十分显著；由图4(b)和图4(c)可以看出当通道平衡时，残差相位的存在引起了杂波残留，且随着信号幅度的增强，残留杂波也近似同比例增强，换句话说幅度越强对残差相位越敏感，因此类似城市的具有强散射静止地物的区域杂波残留将很严重。显然如果能降低残差相位的影响，将会有助于抑制强杂波。

图2 DPCA处理后杂波概率密度分布Fig. 2 DPCA clutter probability density distribution

杂波残差相位(在ATI-SAR中称为杂波干涉相位)分布的中心偏离Y轴一个角度θ，且大部分残差相位集中于θ附近，角度θ的存在很显然会使DPCA处理后的杂波残留更加严重，角度θ可近似由通道复相关系数的相位角给出，如式(4)所示[12]。

很容易想到将干涉相位Δϕ减去偏角θ，即对干涉相位进行校正，将干涉相位分布的中心搬移到Y轴，然后用校正后的干涉相位对DPCA幅度进行非线性加权，将有可能使杂波抑制效果得到改善，并尽可能保留动目标信息。

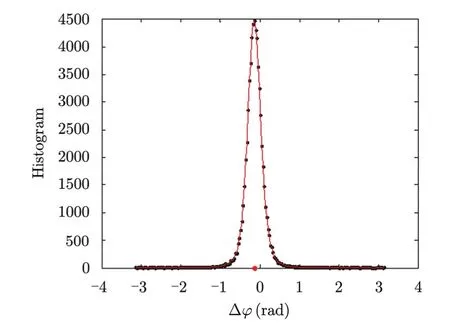
图3 杂波残差相位分布图Fig. 3 Residual phase difference histogram

图4 干扰因素对DPCA的影响Fig. 4 Interference for DPCA

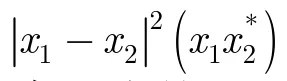
在借鉴以上方法优点的基础上本文提出改进的DPCA方法(称之为加权DPCA)，用校正后的干涉相位对DPCA幅度进行正弦调制，

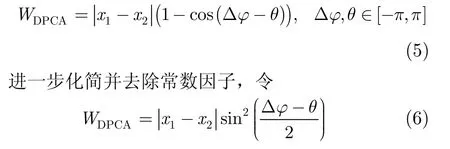
DPCA幅度经过非线性变换后，目标和杂波的DPCA幅度都得到衰减，衰减系数为：

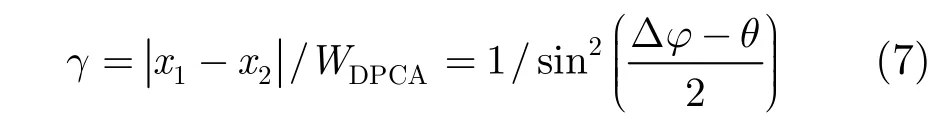
为了从理论上分析干涉相位校正后加权DPCA对比DPCA的优势，我们假设两通道已平衡，即则式(6)可写成以下形式[16]：

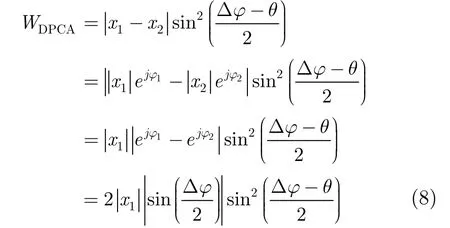
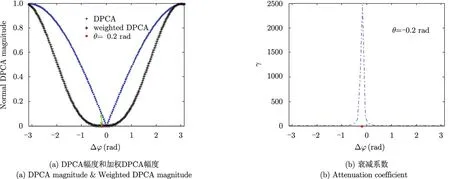
图5 DPCA与加权DPCA理论对比Fig. 5 Theoretical comparison of DPCA and weighted DPCA

如图5(a)和图5(b)所示，假设取θ=-0.2，即杂波干涉相位大部分分布于-0.2附近，随着干涉相位绝对值的不断增大，衰减系数逐渐变小，对比图3和图5(b)可知，加权DPCA对杂波集中区域的衰减程度明显高于杂波非集中区域，换句话说，目标的衰减程度要远小于杂波的衰减程度，图5(a)中绿色双箭头所指长度即为传统DPCA的残留杂波，经过加权DPCA方法处理后可明显看出残留杂波主分布区域被很好地抑制。当然对残留杂波抑制的同时，干涉相位很小的可能的运动目标也会被作为杂波抑制掉，不过，这些运动速度极慢的微动目标往往并不是军事监视关心的重点且数量有限，虽然牺牲了微动目标的检测能力却可以使虚警率显著降低。图6给出了加权DPCA的流程图。

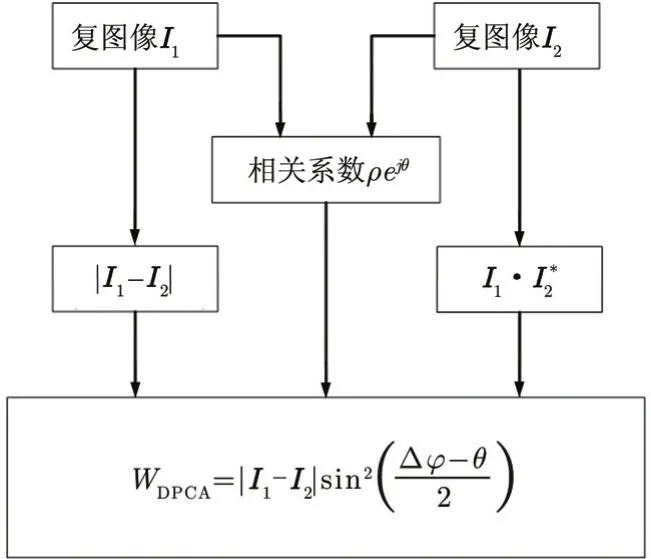
图6 加权DPCA杂波抑制流程图Fig. 6 Framework of clutter rejection with weighted DPCA

4 实验验证

4.1 实验数据

实验采用美国航空太空总署(NASA)的AirSAR C波段复图像数据(已完成通道均衡校正以及配准)，平台及雷达相关参数如表1所示。图7(a)和图7(b)是从同一幅单通道数据中提取的两幅子图像，图7(a)指示城市区域(非均匀地物区域)，图7(b)指示包含公路的郊区(均匀地物区域)，为了方便展示，两幅示意图均对原始幅度数据进行了20倍的对数拉伸，图7(c)和图7(d)分别是城市区域和郊区的干涉相位统计分布。由于缺乏地面运动目标真实集，尤其无法完全确认城市区域中哪些像素是运动目标，通过幅度、干涉相位，以及SAR图像判读等知识，我们认为图7中所有的绿色框所示区域为运动目标。

4.2 杂波抑制效果对比

图8(a)～图8(d)为对应图7(a)的传统DPCA法与加权DPCA法的杂波抑制效果对比，图9(a)～图9(d)为对应图7(b)的传统DPCA法与加权DPCA法的杂波抑制效果结果对比。

表1 平台及雷达主要参数Tab. 1 Parameters of platform and radar

从图8(a)和图8(b)的对比可以看出，经过加权DPCA处理后，背景更加纯净，残留杂波被明显抑制。图8(c)和图8(d)分别为对应图8(a)和图8(b)的杂波抑制结果量化值，从中也可看出两个运动目标幅度只被轻微抑制，而大部分杂波都得到了较大程度的抑制。需要说明的是由于城市中的运动目标真实情况无法实地调查，我们并不能十分确切地判断那些疑似运动目标的真实属性，但这并不妨碍实验对该方法杂波抑制能力的证明，为了便于观察，本文只展示了3维视图的方位向视图。

图7 SAR示意图及干涉相位统计分布Fig. 7 SAR schematic image and Interferometric phase histogram

图9(a)～图9(d)中展示了非均匀区域的杂波抑制效果对比，为了充分证明该方法对非均匀地物场景和均匀地物场景均有效，我们选取了城市附近的郊区场景进行杂波抑制对比试验。图7(b)和图9(a)，图9(c)中黄色框标定的区域为路边临时停车场，亮点为静止车辆或油罐(强杂波)，从图9(a)和图9(c)中看出经过传统DPCA方法处理后，该静止目标没有被抑制。从图9(c)和图9(d)的对比中可以看出，经过加权DPCA处理后静止强杂波被成功抑制(图 9(c)中黄色框标定区域被成功抑制)，而且大部分平坦区域的杂波幅度被抑制到更低水平。

进一步对比图9(a)和图9(b)发现，有部分树丛区域的像素点经过加权DPCA处理后相比周围环境比较凸现，被抑制程度较轻(图9(d)中红色圈所标)，这是因为郊区的树丛由于受风的影响而摆动，相比周围草地必然会产生更加显著的相位差，根据前文理论分析可知这些像素点的衰减程度不如草地等静止地物。

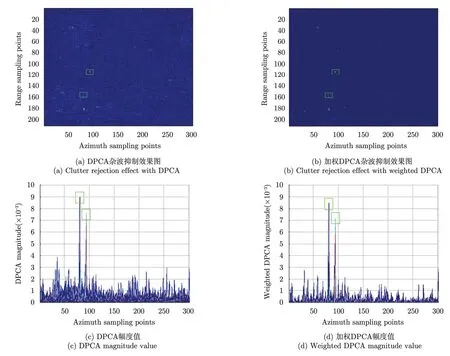
图8 非均匀区域杂波抑制效果对比Fig. 8 Comparison of clutter rejection results in heterogenous terrain

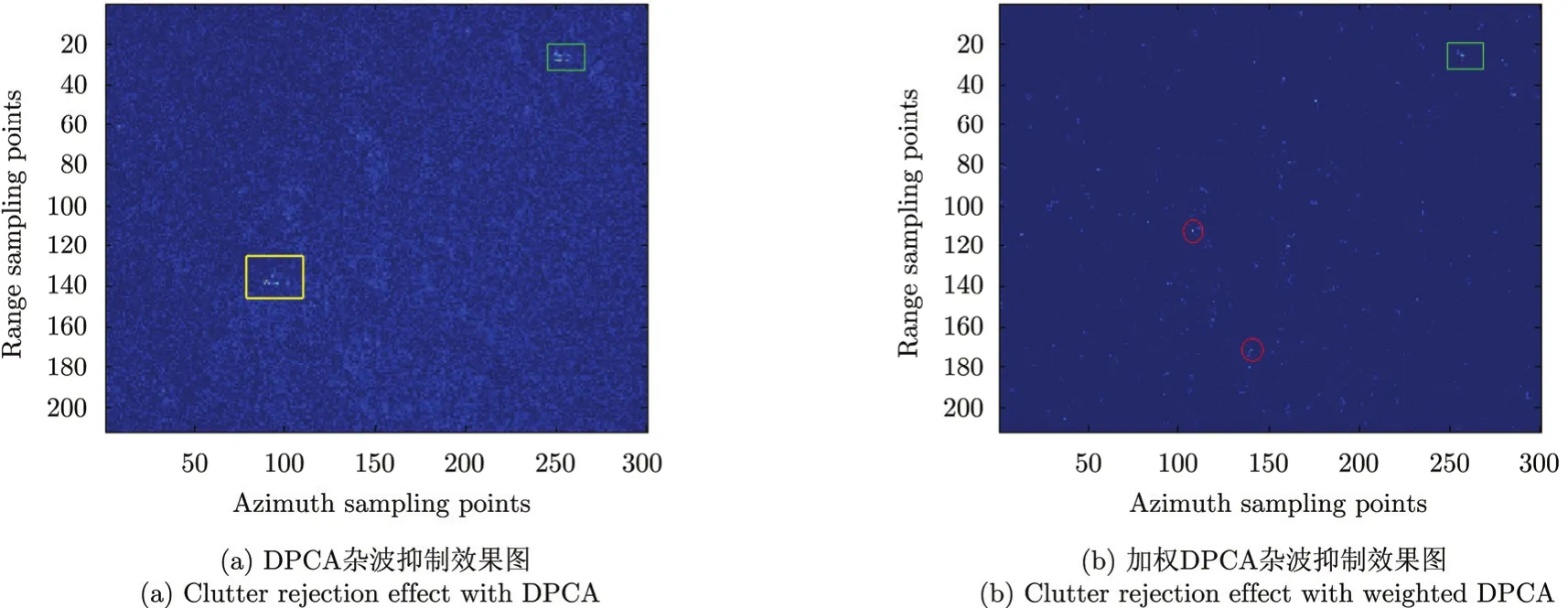
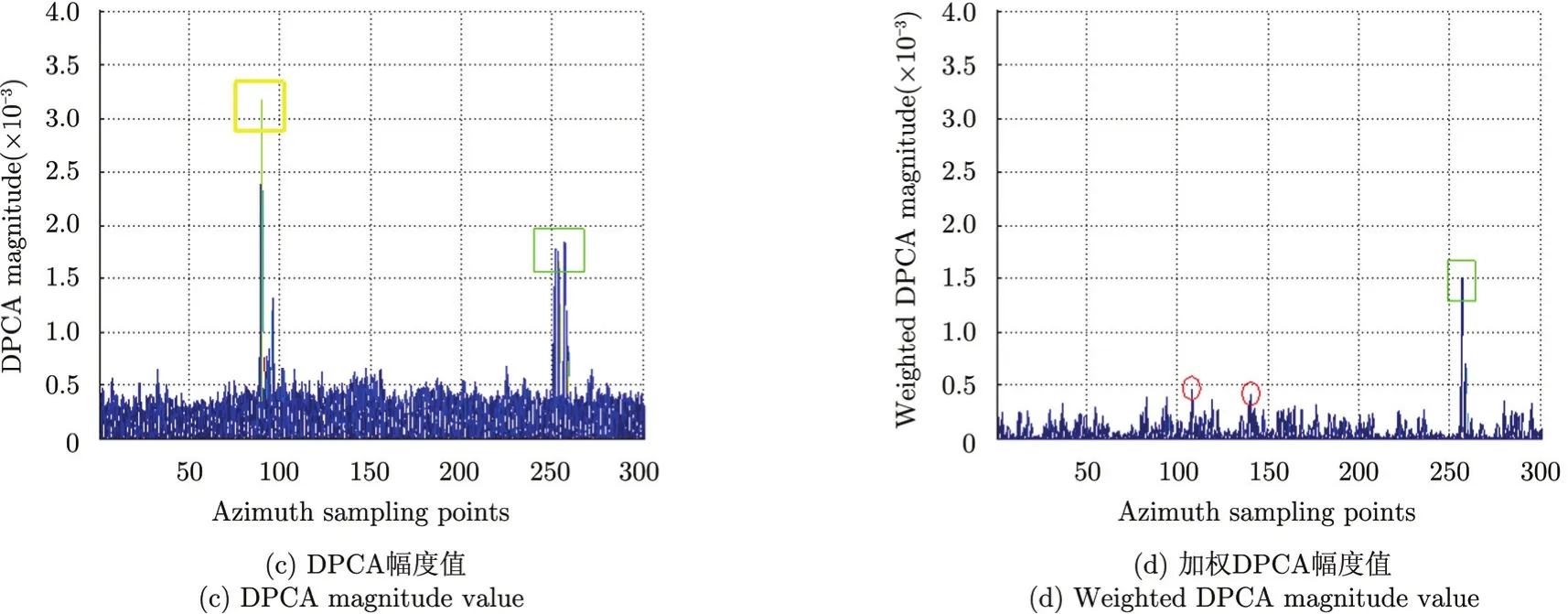
图9均匀区域杂波抑制效果对比Fig. 9 Comparison of clutter rejection results in homogenous terrain

5 结束语

本文结合双通道DPCA复图像数据的干涉相位提出了一种SAR-GMTI杂波抑制新方法，该方法不改变双通道DPCA的物理结构，利用校正后的双通道干涉相位对DPCA幅度进行非线性加权，降低了残差相位对DPCA杂波抑制的影响，均匀区域和非均匀区域的实测数据均证明了本文方法比传统DPCA方法具有更优的杂波抑制能力，有望被用来解决SAR-GMTI的杂波抑制问题。

[1]王永良. 空时自适应信号处理[M]. 北京: 清华大学出版社,2000: 1-20. Wang Yong-liang. Space-Time Adaptive Signal Processing[M]. Beijing: Tsinghua University Press,2000: 1-20.

[2]Ender J H G. Space-time processing for multichannel synthetic aperture radar[J]. Electronics & Communication Engineering Journal,1999,11(1): 29-38.

[3]Klemm R. Applications of Space-Time Adaptive Processing[M]. London: The Institution of Electrical Engineers,2004: 177-206.

[4]王永良,陈建文,吴志文. 现代DPCA技术研究[J]. 电子学报,2000,28(6): 118-122.Wang Yong-liang,Chen Jian-wen,and Wu Zhi-wen. Research on modern DPCA techniques[J]. Acta Electronica Sinica,2000,28(6): 118-122.

[5]孟祥东. 空时二维自适应信号处理与动目标检测[D]. [博士论文],西安电子科技大学,2009.Meng Xiang-dong. Space-time adaptive processing and moving target indication[D]. [Ph.D. dissertation],Xidian University,2009.

[6]Morena L C,James K V,and Beck J. An introduction to the RADARSAT-2 mission[J]. Canadian Journal of Remote Sensing,2004,30(3): 221-234.

[7]Gierull C H and Sikaneta I. Two-step detector for RADARSAT-2’s experimental GMTI mode[J]. IEEE Transactions on Geoscience and Remote Sensing,2013,51(1): 436-454.

[8]Coe D J and White R G. Moving target detection in SAR imagery: experimental results[C]. IEEE International Radar Conference,British,1995: 644-649.

[9]Shen Chiu and Livingstone C. A comparison of displaced phase centre antenna and along-track interferometry techniques for RADARSAT-2 ground moving target indication[J]. Canadian Journal of Remote Sensing,2005,31(1): 37-51.

[10]保铮. 雷达成像技术[M]. 北京: 电子工业出版社,2005: 318-319.Bao Zheng. Radar Imaging Technology[M]. Beijing: Electronic Industry Press,2005: 318-319.

[11]郑明洁. 合成孔径雷达动目标检测和成像研究[D]. [博士论文],中国科学院电子学研究所,2003: 79-89.Zheng Ming-jie. Study on detection and imaging of moving target with synthetic aperture radar[D]. [Ph.D. dissertation],Institute of Electronics,Chinese Academy of Sciences,2003: 79-89.

[12]Lee J S,et al.. Intensity and phase statistics of multi-look polarimetric and interferometric SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing,1994,32(5): 1017-1028.

[13]赵宁,李景文. 机载SAR加权ATI地面慢速运动目标检测方法[J]. 雷达科学与技术,2007,5(3): 189-193.Zhao Ning and Li Jing-wen. A weighting ATI ground slow velocity moving target detection method for airborne SAR[J]. Radar Science and Technology,2007,5(3): 189-193.

[14]时公涛. 基于干涉图的多通道SAR地面慢动目标自动检测技术研究[D]. [博士论文],国防科学技术大学,2009: 30-51.Shi Gong-tao. Study on automatic detection of moving slowly target based on multi-channel SAR interferogram[D]. [Ph.D. dissertation],National University of Defense Technology,2009: 30-51.

[15]Gao Gui and Shi Gong-tao. The CFAR detection of ground moving target based on a joint metric of SAR interferogram’s magnitude and phase[J]. IEEE Transactions on Geoscience and Remote Sensing,2012,50(9): 3618-3624.

[16]Livingstone C E,Sikaneta I,and Gierull C H. An airborne synthetic aperture radar (SAR)experiment to support RADARSAT-2 ground moving target indication (GMTI)[J]. Canadian Journal of Remote Sensing,2002,28(6): 794-813.

A Clutter Suppression Approach for SAR-GMTI Based on Dual-channel DPCA

Wang Xiao-yang Gao Gui Zhou Shi-lin Zou Huan-xin
(College of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)

The Displaced Phase Center Antenna (DPCA)technology,a particular form of Space Time Adaptive Processing (STAP),has been widely used in Synthetic Aperture Radar Ground Moving Target Indication (SAR-GMTI). The GMTI performance depends on the capability of clutter rejection but the traditional DPCA technology operated in the complex image domain does not have the appropriate clutter rejection capability for urban areas with strong scattering stationary objects. Hence,interferometry phase is used to weight the DPCA magnitude nonlinearly,and a weighted DPCA clutter rejection approach is proposed,which reduces the interference from residual phase difference. The experimental results suggest that the new approach can improve the clutter rejection compared with the conventional DPCA.

Space Time Adaptive Processing (STAP); Displaced Phase Center Antenna (DPCA); Synthetic Aperture Radar (SAR); Ground Moving Target Indication (GMTI); Clutter rejection

TN958

A

2095-283X(2014)02-0241-08

10.3724/SP.J.1300.2014.13121

2013-12-09收到，2014-02-24改回；2014-03-07网络优先出版国家自然科学基金(41171316)资助课题

*通信作者： 王肖洋 henanwangxiaoyang@163.com

王肖洋(1989-)，男，籍贯：河南，国防科技大学硕士研究生，研究方向为智能信息处理、合成孔径雷达动目标检测。E-mail: henanwangxiaoyang@163.com

高 贵(1981-)，男，籍贯：内蒙古，国防科技大学电子科学与工程学院副教授，研究领域包括合成孔径雷达自动目标识别、SAR图像建模、SAR-GMTI。

周石琳(1965-)，男，籍贯：湖南，国防科技大学电子科学与工程学院教授，博士生导师，研究领域包括计算机视觉及智能信息处理、图像图形处理以及数字摄影测量与遥感等。邹焕新(1973-)，男，籍贯：广东，国防科技大学电子科学与工程学院副教授，研究方向为图形图像处理及数字摄影测量与遥感。