一种基于勒让德拟合的SAR后向投影自聚焦算法

高 阳 禹卫东 冯 锦 郑世超② 杨 亮②

①(中国科学院电子学研究所 北京 100190)

②(中国科学院大学 北京 100049)

Gao Yang①② Yu Wei-dong① Feng Jin① Zheng Shi-chao①② Yang Liang①②

①(Institute of Electronic,Chinese Academy of Sciences,Beijing 100190,China)

②(University of Chinese Academy of Sciences,Beijing 100049,China)

一种基于勒让德拟合的SAR后向投影自聚焦算法

高 阳*①②禹卫东①冯 锦①郑世超①②杨 亮①②

①(中国科学院电子学研究所 北京 100190)

②(中国科学院大学 北京 100049)

对于合成孔径雷达(SAR)成像来说，后向投影(Back Projection,BP)算法是一种十分重要的时域成像方法。然而现有的自聚焦算法都是基于频域成像算法开发的，无法直接用于BP聚焦图像的误差相位估计。针对这一问题，该文提出一种适用于BP图像的自聚焦算法。该算法以图像锐度函数为目标函数，以待估计的相位校正值为自变量，通过坐标下降最优化算法循环迭代获得它们的最优估计。在问题求解中，该算法利用勒让德多项式来拟合目标函数，使得每次迭代的最优解可以解析地获得，避免了低效的线搜索过程。基于仿真数据和实测数据的实验验证了该算法的精确性和有效性。

后向投影算法；勒让德拟合；图像锐度；自聚焦；坐标下降法

Gao Yang①②Yu Wei-dong①Feng Jin①Zheng Shi-chao①②Yang Liang①②

①(Institute of Electronic,Chinese Academy of Sciences,Beijing 100190,China)

②(University of Chinese Academy of Sciences,Beijing 100049,China)

1 引言

作为一种微波有源遥感系统，合成孔径雷达(Synthetic Aperture Radar,SAR)因其全天时、全天候的工作能力而受到越来越广泛的关注，已经被广泛应用到军事侦察、地形测绘、水文研究、环境监测等各个领域[1]。SAR传感器在理想状态下被认为沿着直线轨迹做匀速运动。然而在实际情况下，由于气流的扰动、载体机械振动等因素，载机位置会偏离理想轨迹，从而在处理中引入相位误差，造成图像质量的严重下降[2]。对于雷达运动状态的测量，常通过在系统上加装导航装置来实现[3]。而对于超出导航设备测量精度的运动误差，则必须通过基于回波数据的自聚焦来对相位误差进行估计和补偿。

自聚焦是一种根据回波数据对相位误差进行估计的算法，在SAR成像处理中占据着非常重要的地位。现有的自聚焦算法主要分为两类：第1 类是基于图像特显点的自聚焦算法，第2类是基于图像整体质量的估计算法。对于基于图像特显点的方法，其代表算法为相位梯度自聚焦算法(Phase Gradient Autofocus,PGA)[4]。该算法利用多个强点目标的相位历程来对相位误差进行估计。由于其不基于任何相位误差模型，因此PGA算法对高阶和低阶误差均有很好的补偿能力。后一类基于图像质量的估计算法主要将图像的整体信息作为评价准则，通过调节相位的估计值使图像质量达到最优来确定补偿的相位。常用的评价准则包括：最小熵[5]，最大对比度[6,7]，最大锐度[8]等。根据误差模型的不同，该算法又可分为基于参数[9]和不基于参数的两类[5,7]，分别用于估计低频和高频误差。相对于PGA算法，由于该类算法不基于孤立强点，所以其在低信噪比和低对比度的条件下更具有鲁棒性，能够取得更好的聚焦效果。

以上提到的各种自聚焦方法都是基于频域成像算法提出的。频域成像算法认为距离压缩后的信号与最终图像之间存在着傅里叶变换对的关系。因此，传统自聚焦算法的实现基于以下两个条件：(1)包络误差对图像的影响可以忽略；(2)图像与距离相位历史数据具有傅里叶变换对关系[10]。自聚焦就是对存在于距离压缩信号域的数据相位误差进行估计，从而实现图像的重新聚焦[2]。相对于频域算法来说，后向投影(Back Projection,BP)算法作为一种时域成像算法，其在成像精度、对复杂轨迹和地表起伏的适应性上有着天然的优势[11]。由于在时域算法中不存在明显的傅里叶变换关系，因此无法将传统自聚焦方法直接应用于BP成像数据。为了解决这一问题，文献[10]和文献[12]对BP成像中的信号性质进行了分析。经研究发现，当图像在极坐标或伪极坐标格式下的时候，傅里叶变换对的关系是近似满足的。这样就可以针对(伪)极坐标下的图像设计相应的自聚焦算法[10,12]。

以上提到的算法均基于傅里叶变换对的关系，而对于不满足该条件下的自聚焦方法却缺乏足够的研究。为了弥补上述不足，本文提出了一种针对BP聚束SAR图像，不依赖于傅里叶变换对关系的时域自聚焦算法。该算法根据反投影原理并根据图像锐度值准则实现了在直角坐标系下的BP图像自聚焦。作者利用图像整体质量评价方法的鲁棒特性，通过最大化图像平方锐度值来达到对相位误差的估计。平方锐度准则不仅在多种场景中表现出了稳定的性能[8]，而且在特定条件下还可以实现对误差的最大似然估计[13]。为了求解最大化图像锐度的问题，算法采用坐标下降策略[14]来逐个优化各相位变量。另外，通过对每次迭代的目标函数进行勒让德多项式拟合，我们可以解析地得到最优相位校正量，相对于线搜索方式来说极大地提高了计算效率。本文首先研究了相位误差在BP成像算法中的表现形式，然后对坐标下降算法以及勒让德多项式拟合进行了推导，给出了误差相位的迭代表达式，最后对该算法的实验结果进行了分析。仿真和实测数据表明，该算法具有很高的估计精度和收敛速度，可以很好地与BP算法结合进行误差相位估计。

2 信号模型分析

如图1所示为机载SAR的几何关系示意图。蓝色实线为雷达实际运动轨迹，红色虚线为导航设备测量获得的运动轨迹。Rp(η)和p(η)分别是η时刻天线相位中心到点目标P的测量斜距和实际斜距。则η时刻雷达位置的测量误差为：

2.1 BP成像模型

假设雷达发射的线性调频信号形式为：

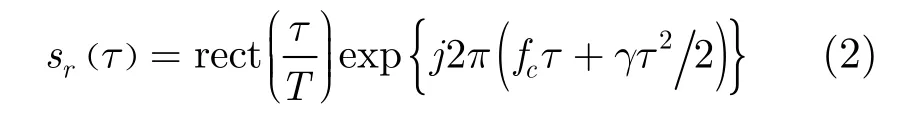
其中τ为距离向快时间；T为脉冲宽度；fc为载频；γ为发射信号调频率。该发射信号经过反射系数为εp，瞬时距离为p(η)的地面点反射后，由雷达进行接收。接收的回波信号，经过距离压缩后的表达形式为：

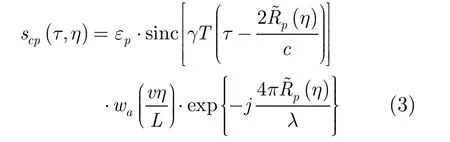
其中η为方位向慢时间；wa表示方位向信号包络；c为光速；λ=cfc为信号波长。这里采用BP算法来对地面照射区域进行成像处理，根据BP成像算法理论，经过后向投影重构得到的地面P点图像可以通过式(4)来获得

图1 SAR成像几何模型Fig. 1 Geometry model of SAR imaging

其中rp表示P点的最短斜距。由于雷达回波信号以数字的形式进行存储和处理，所以可以将上式写成离散形式

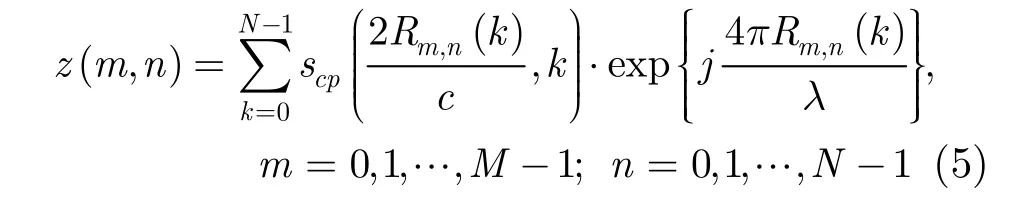
式中，(m,n)为P点在图像中的位置；Rm,n(k)表示方位向采样k时刻天线相位中心到P点的瞬时斜距；N和M分别为方位向和距离向采样点数。

对于窄测绘带而言，可以认为由斜距带来的误差是距离向空不变的，因此可以统一用ϕ(k)= -4πΔRm,n(k)/λ来表示由斜距误差引入的相位。该相位误差如果不补偿到一定的精度，将导致最终图像分辨率降低、几何畸变以及对比度损失等现象。令

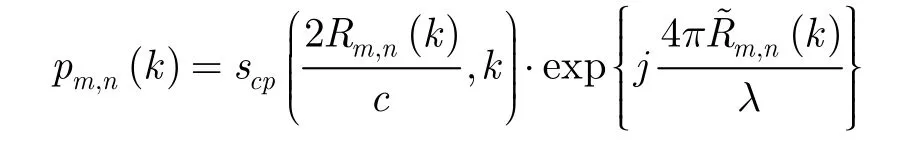
表示经过理想反投影操作后的信号，那么式(6)可以简化为：

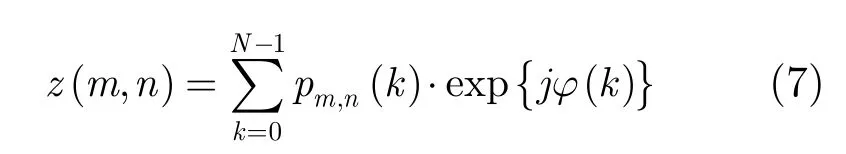
自聚焦的任务即从雷达数据中估计出误差相位ϕ(k)并进行补偿，进而得到聚焦的图像。假设ϕ={ϕ0ϕ1…ϕN-1}表示对误差相位ϕ(k)的估计，那么误差相位校正后的图像可以表示为：

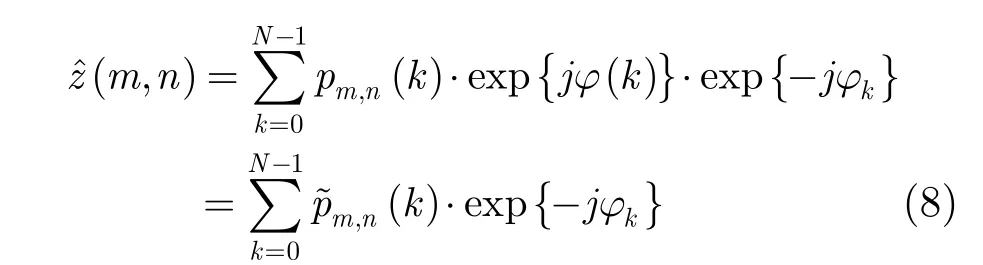
2.2 图像锐度

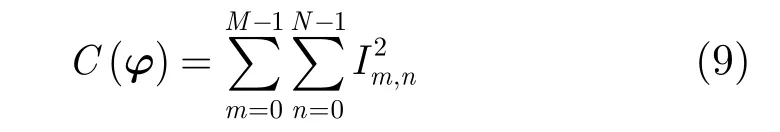
当图像散焦时图像的锐度较低，而当图像聚焦良好时对应的锐度值较高。所以这里可以把图像锐度作为估计相位的目标函数，那么目标函数可以构造为：因此，基于图像锐度最优的自聚焦就是通过使图像锐度达到最大来实现对误差相位的估计的过程。

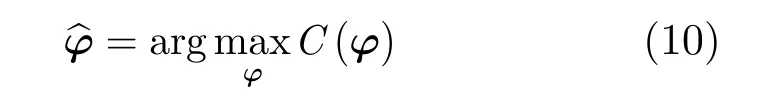
3 适用于BP聚焦图像的自聚焦算法

式(10)定义了一个多变量的优化问题。考虑到该方程没有闭式解存在，这里利用坐标下降优化方法来寻找该问题的最优解。坐标下降法是一种针对多变量优化的有效策略。在实现过程中，该方法沿着每个变量定义的方向逐一进行搜索，每次优化针对单个变量进行，其它变量值保持不变[14]。找到当前变量对应于目标函数的极值解后，继而对下一变量进行搜索。由于各变量之间并不能保证完全独立，因此针对全部变量的搜索过程需要重复多次，即多次迭代才能找到问题的最优解。

这里前k-1个变量已经在本次迭代中进行了更新。从式(11)中可以看出，由于只有第k个参数可变，而其它变量在本次估计中保持恒定，这样多变量优化的问题就简化为一个单变量的优化问题

此时，关于变量ϕ的重构图像可以表示为：

其中，Xmn表示除了第k个反投影信号之外，其它经校正后的反投影信号之和；Ymn表示第k个未经校正的反投影信号。相应的图像锐度可以表示为：

Re[·]和Im[·]分别表示复数据的实部和虚部。

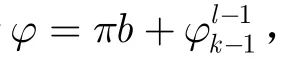
对式(16)进行勒让德多项式拟合，可以得到

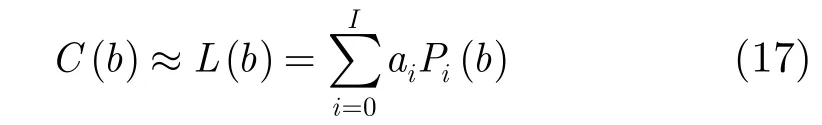
式中，I表示勒让德多项式的最高阶数；Pi(b)和ai分别表示第i阶勒让德多项式和其对应的系数。为了在满足拟合精度的前提下尽可能地提高计算效率，这里保留前4阶勒让德展开式。此时，从P0(b)到P4(b)的形式为：

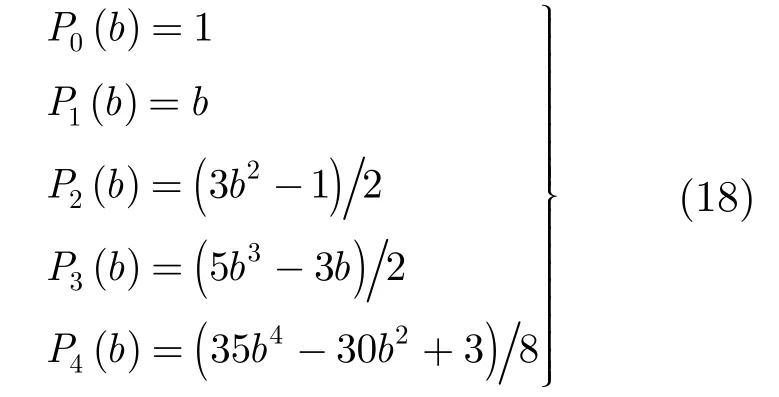
从式(17)和式(18)中可以看出，L(b)表现为4阶多项式的形式，因此L(b)的极值可以通过求解其1阶导数L′(b)，并令其为零来求得。将式(18)代入式(17)，并令L′(b)=0，可以得到

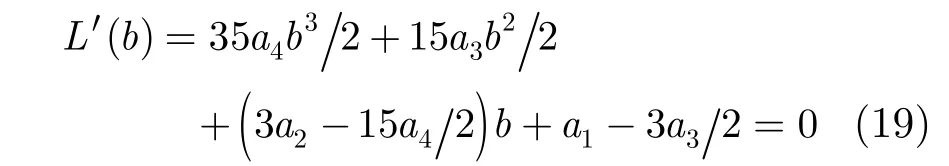
对于式(19)给出的一元3次方程来说，文献[15]给出了其根的闭式表达形式，这意味着可以通过解析的方法来得到其根的精确解，从而避免了复杂而低效的数值求解过程。由于一元3次方程最多可以给出3个实数解，在实际应用中可以通过考察其2阶导数L′′(b)＜0来选择代表目标函数极大值的根bop。找到式(19)方程的根后，对应的相位估计值可以由式(20)来进行更新

为了验证勒让德多项式拟合的有效性，利用典型的SAR数据来对某一反投影信号在不同相位校正后的图像锐度来进行考察。图2表现了图像锐度的1阶导数相对校正相位的变化情况。由于图像锐度的极大值在导数等于0处获得，因此曲线与横轴交点处的相位值即为极大值对应的校正相位。需要说明的是，图2中在真实校正相位点的两侧仍有两个导数为0的伪相位值存在，对应式(19)的另外两个根。由于真实相位值和伪相位值对应的2阶导数具有不同的符号，所以可以通过考察其2阶导数来对伪相位值进行剔除。图中蓝色实线表示实际图像锐度目标函数，红色虚线表示经过勒让德拟合后的函数曲线。从图2中可以看出4阶勒让德多项式可以很好地对实际目标函数进行拟合，并且对于极值点附近具有较高的拟合估计精度。

4 实验结果及分析

下面分别通过SAR仿真数据和实测数据处理来验证本文算法的精确性和有效性。

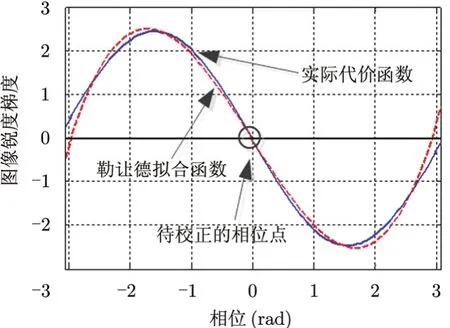
图2 实际图像锐度梯度目标函数曲线和勒让德拟合函数曲线的对比Fig. 2 Comparison of actual function and Legendre fitting function of image sharpness deviation

4.1 SAR仿真数据处理结果与讨论

仿真处理中选用X波段的SAR数据来作为测试数据。该原始数据经过BP成像后的结果如图3(a)所示，大小为512×512像素。从图3(a)中可以看到，原始数据经BP成像处理后具有良好的聚焦效果。在试验中，我们尝试在该数据距离压缩前的信号中添加一个已知的宽带相位误差，之后利用本文提出的自聚焦算法来对该相位误差进行估计，进而验证本文算法的有效性和精确性。

在原始数据中添加的宽带相位误差信号如图4中实线所示，图3(b)展示了添加相位误差后对应的散焦图像。针对添加相位误差后的图像，采用本文算法来进行自聚焦处理。在处理中，相位误差的原始估计值设为0，经过4次迭代后估计出的相位误差值和重聚焦后的图像分别如图4中虚线和图3(c)所示。图5展示了该算法每次迭代时图像锐度值(Image Sharpness Value,ISV)的变化情况，从图5中可以发现：该算法首次迭代即能对绝大部分相位误差进行有效地估计，并且经过4次迭代就可以基本恢复原始图像锐度，表现出了非常快的收敛速度。对比图3(a)和图3(c)，可以看到两者具有相同的视觉效果，其锐度值达到了一致。同时将图4中估计的相位误差与添加的相位误差进行比较也可以看到，两条曲线基本重合。经测试，其估计的相位弧度值的均方误差(Mean Square Error,MSE)为0.029，说明该自聚焦算法具有很高的估计精度。

另外，为了测试利用勒让德拟合策略解析求解相位校正值的方法相对于传统线搜索方式的性能提升情况，这里我们采用Wolfe-Powell(W-P)线搜索方式[16]对上述数据进行对比试验和分析。W-P搜索方式在最优化方法中，是一种典型的线搜索策略，它可以通过调整判断准则系数有效地控制搜索速度和精度。由于添加的相位误差已知，所以在实验中，估计相位的均方误差将作为算法精确度的评价指标。表1给出了本文算法和W-P方法的对比试验结果。在实验中，本文算法经过21.3 s的时间停止迭代。之后，针对W-P方法进行测试，在运行大约相同时间的情况下，给出的估计相位均方误差为0.639，远大于本文算法的剩余误差。在针对W-P算法的第2次实验中，我们选择与本文算法相同的均方误差值作为迭代停止的标准。从表1中可以看到，W-P算法消耗约4.6倍于本文算法的运行时间才达到相应的计算精度。从而可以发现，本文算法相对于传统线搜索方法来说具有较好的估计速度和估计精度。

图3 SAR仿真数据处理结果Fig. 3 Processing results of simulated SAR data

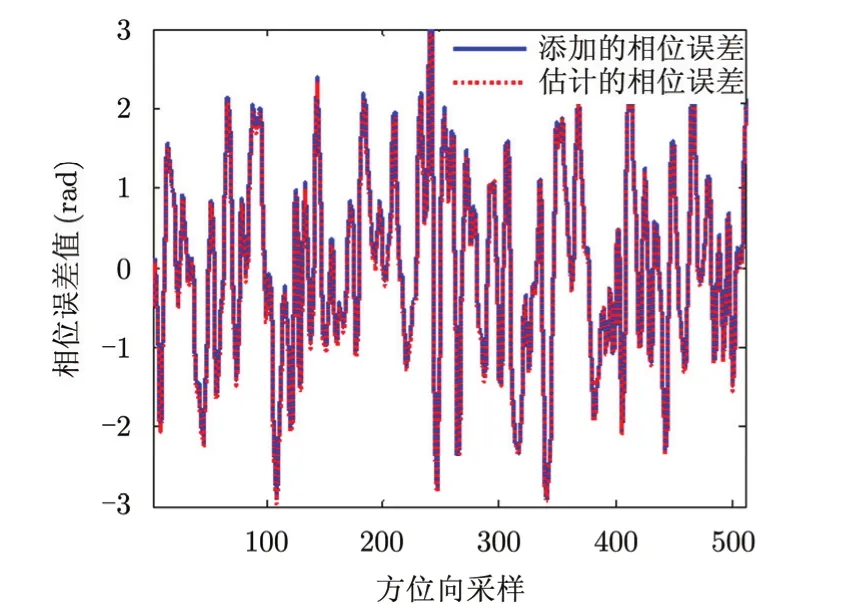
图4 相位误差曲线比较Fig. 4 Comparison of actual applied phase error and estimated phase error

图5 图像锐度值随迭代次数的变化曲线Fig. 5 Sharpness versus iteration of the algorithm

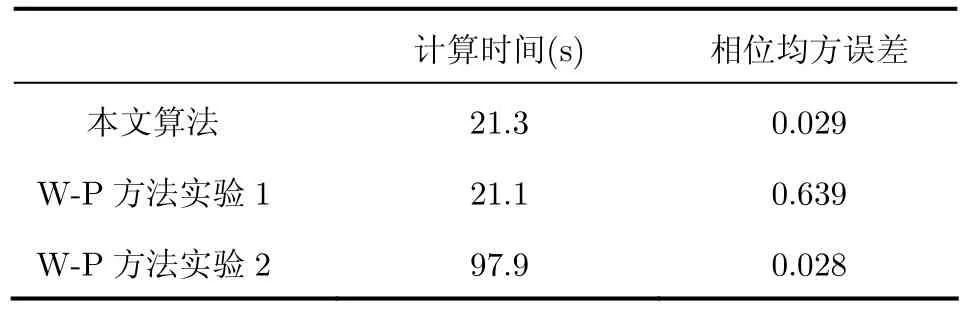
表1 本文算法与W-P方法在运算速度和精度上的实验对比结果Tab. 1 Accuracy and speed comparison for W-P and the proposed algorithm

需要说明的是，本文算法基于时域的成像方式从实现本质上说属于时域自聚焦的方法。由于该自聚焦方法不依赖于图像与距离相位历史数据之间的傅里叶变换对关系，即处理中没有利用快速傅里叶变换等技术来提高运算效率，其算法相比于频域自聚焦算法，如PGA算法，具有较高的计算量。为了进行对比，我们利用频域成像算法对同一块数据进行成像处理，之后对同样大小场景的数据块利用PGA算法进行自聚焦，来测试两种自聚焦算法在计算效率上的差别。经过测试，PGA消耗大约2.3 s的时间完成了对同样大小数据块的处理，低于本文方法所需要的时间。从中也可以看出，本文提出的时域算法计算效率仍低于PGA这样的频域算法，因此在接下来的工作中，需要进一步研究提升其运算效率的策略。

4.2 SAR实测数据处理结果

为了进一步验证本文算法的有效性，下面使用该算法对实测数据进行处理。该实测数据为某机载X波段SAR系统。由于载机飞行过程极易受到气流等非理想因素的干扰，从而引入未知的相位误差，对最终的成像质量造成影响。本文选取该系统录取的一段农村地区的图像数据，该数据图像包含了农田、小路、建筑、树木等场景。图6(a)为原始数据直接进行BP成像后的结果，水平方向是方位向，垂直方向是距离向。由于载机飞行姿态的不稳定，从图中可以看到，未经任何重聚焦处理的图像存在严重的方位向散焦，极大影响了对地物目标的有效判读。图6(b)为经过本文自聚焦处理后的雷达图像。通过对比可以发现，图6(b)中的图像的聚焦质量有了大幅度的提升，树木、建筑物、小路、农田、阴影等都清晰可见，点目标不存在明显的散焦现象。由此可见，本文算法可以很好地处理BP算法生成的图像。该处理结果表明，本文算法适用于实际机载SAR的BP成像处理，可以有效地对相位误差进行估计和补偿。

5 结束语

图6 原始图像与自聚焦后图像对比Fig. 6 Comparison of original and recovered images

自聚焦处理是SAR成像不可缺少的一个步骤。针对BP算法生成的SAR图像，作者提出了一种基于图像锐度最优的自聚焦算法。本文首先对相位误差在BP算法中的存在形式进行了分析，然后基于最大图像锐度准则给出了问题的最优化模型。对于该最优化问题，本文算法采用了坐标下降优化方法来作为求解策略。同时，勒让德多项式拟合的应用实现了在保持估计精度的同时可以解析地求解极值相位的能力。由于该算法对相位误差的形式没有做任何限制，因此其可以处理各种低频和高频误差。仿真和实测数据实验表明，该算法具有很高的估计精度和收敛速度，从而验证了本文方法的有效性和可行性。

需要说明的是，本文算法设计主要针对小场景非空变相位误差进行估计。对于宽波束宽测绘带下的高分辨率数据来说，处于不同斜距和方位向位置的目标具有不同的相位误差，此时就需要结合雷达成像几何对处于不同位置下目标的相位误差进行分析和补偿。由于BP时域成像算法能够很方便地对宽波束SAR信号进行处理，所以在接下来的工作中，将针对该自聚焦算法在大场景空变相位误差情况下的估计方式，以及在如何进一步提高计算效率的问题上进行重点研究。

[1]邓云凯,赵凤军,王宇. 星载SAR技术的发展趋势及应用浅析[J]. 雷达学报,2012,1(1): 1-10. Deng Yun-kai,Zhao Feng-jun,and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars,2012,1(1): 1-10.

[2]Carrara W G,Goodman R S,and Majewski R M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms[M]. Boston: MA,Artech House,1995,Ch. 5: 203-236.

[3]郭振永,邓云凯,涂国防. 基于IMU数据与双星定位系统组合的机载SAR运动补偿[J]. 电子与信息学报,2007,29(8): 1802-1804. Guo Zhen-yong,Deng Yun-kai,and Tu Guo-fang. Airborne SAR motion compensation based on IMU data and GEOSTAR integrated system[J]. Journal of Electronics & Information Technology,2007,29(8): 1802-1804.

[4]Wahl D E,Eichel P H,Ghiglia D C,et al.. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems,1994,30(3): 827-835.

[5]Li X,Liu G,and Ni J. Autofocusing of ISAR image based on entropy minimization[J]. IEEE Transactions on Aerospace and Electronic Systems,1999,35(4): 1240-1252.

[6]武昕伟,朱兆达. 利用对比度最大化实现SAR 图像自聚焦[J].现代雷达,2002,24(3): 20-22. Wu Xin-wei and Zhu Zhao-da. A novel autofocus algorithm for SAR imagery by contrast maximization[J]. Modern Radar,2002,24(3): 20-22.

[7]Kolman J. PACE: an autofocus algorithm for SAR[C]. IEEE International Radar Conference,Arlington,VA,USA,2005: 310-314.

[8]Fienup J R and Miller J J. Aberration correction by maximizing generalized sharpness metrics[J]. Journal of the Optical Society of America A: Optics,Image Science,and Vision,2003,20(4): 609-620.

[9]Berizzi F,Corsini G,Diani M,et al.. Autofocus of wide azimuth angle SAR images by contrast optimization[C]. In Proceedings of Geoscience and Remote Sensing Symposium,IGARSS’96,Kincoln,NE,USA,1996: 1230-1232.

[10]Zhang L,Li H,Qiao Z,Xing M,et al.. Integrating autofocus techniques with fast factorized back-projection for highresolution spotlight SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters,2013,10(6): 1394-1398.

[11]Frey O,Magnard C,Ruegg M,et al.. Focusing of airborne synthetic aperture radar data from highly nonlinear flight tracks[J]. IEEE Transactions on Geoscience and Remote Sensing,2009,47(6): 1844-1858.

[12]Jakowatz C V and Wahl D E. Considerations for autofocus of spotlight-mode SAR imagery created using a beamforming algorithm[C]. Proceedings of SPIE-Algorithms Synthetic Aperture Radar Imagery XVI,2009,7337: 73370A-1-73370A-9.

[13]Schulz T J. Optimal sharpness function for SAR autofocus[J]. IEEE Signal Processing Letters,2007,14(1): 27-30.

[14]Jorge N and Stephen J W. Numerical Optimizations[M]. New York: Springer-Verlag,1999,Ch. 3 : 53-55.

[15]数学手册编写组. 数学手册[M]. 北京: 高等教育出版社,1979,Ch. 3: 88-89.

[16]袁亚湘,孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社,1997,Ch. 2: 94-107.

A SAR Back Projection Autofocusing Algorithm Based on Legendre Approximation

The Back Projection (BP)algorithm is a very important time-domain methodology for Synthetic Aperture Radar (SAR)imaging. However,conventional autofocus techniques are based on frequency-domain imaging algorithms,and can not be directly applied to BP imagery for error phase estimation. In this paper,an autofocus algorithm for BP imagery is proposed. The algorithm takes image sharpness as an objective function,and employs the coordinate descent optimization scheme to obtain the optimum phase-corrected variables by iterations. In the implementation,with a Legendre approximation of the objective function,the optimal phase estimation can be found analytically for each parameter within an iteration,avoiding computationally expensive line-search procedures. The experimental results with both simulated and measured data confirm the accuracy and effectiveness of the proposed algorithm.

Back Projection (BP)algorithm; Legendre approximation; Image sharpness; Autofocus; Coordinate decent

TN958

A

2095-283X(2014)02-0176-07

10.3724/SP.J.1300.2014.14011

2014-01-15收到，2014-03-05改回，2014-03-14网络优先出版

国家国防科技工业局重点专业技术创新课题(D040103)资助课题

*通信作者： 高阳 gaoyang0209@mails.ucas.ac.cn

高 阳，男，籍贯河北，中科院电子所博士研究生，主要研究方向为机载高分辨率SAR成像处理和运动补偿技术。

E-mail: gaoyang0209@mails.ucas.ac.cn

禹卫东(1969-)，男，研究员，博士生导师，研究方向为SAR系统及其理论、SAR信号处理、电路设计等。

冯 锦(1970-)，男，副研究员，长期从事合成孔径雷达成像处理技术的研究。

郑世超，男，山东日照人，中科院电子所博士研究生，主要研究方向为广域监视信号处理。

E-mail: jerryiszsc@163.com

杨 亮，男，山东烟台人，中科院电子所博士研究生，主要研究方向为合成孔径雷达原始信号模拟。

E-mail: yangliang_mail@163.com