一种基于联合稀疏恢复的空时自适应处理方法

段克清 王泽涛 谢文冲 高 飞 王永良

①(空军预警学院 武汉 430019)

②(国防科学技术大学电子科学与工程学院 长沙 410073)

1 引言

机载相控阵雷达体制下，空时自适应处理(Space-Time Adaptive Processing, STAP)可实现对强杂波的有效抑制以及慢速运动目标的检测[1,2]。该技术需利用相邻多个距离门数据(训练样本)估计待检测距离门杂波协方差矩阵(Clutter Covariance Matrix, CCM)，进而计算空时自适应滤波器权系数。根据RMB (Reed-Mallett-Brennan)准则，为使得由CCM估计误差所带来的杂波抑制性能损失小于3 dB，所需独立同分布训练样本数至少为2倍系统自由度[3]。在实际应用中，由于机载雷达往往面临复杂多变的下视场景，常常难以获取足够的均匀训练样本，因此小样本、高性能STAP算法是目前该领域中的热点研究方向。

近年来，压缩感知或稀疏恢复技术被广泛应用于信号处理领域，并初步应用于机载雷达STAP技术中[4－10]。由于天线的方向性，杂波在空时 2维谱上的分布是稀疏的，因此可利用少量甚至单个训练样本基于超完备字典来获取空时谱上强杂波点的位置，即稀疏系数中的非零元素位置。超完备字典可利用超分辨空时2维导向矢量构造，求解稀疏系数的问题实则为稀疏约束下欠定方程求解问题。针对该问题的求解目前主要有3种途径，即凸优化方法[11－13]、贪婪算法[14－16]和 FOCUSS 算法[17]。其中，贪婪算法运算量较小，算法性能比较稳定，应用较为广泛，因此本文重点讨论贪婪算法在STAP技术中的应用。目前，文献[6-8]主要探讨了利用单样本恢复或多个样本分别恢复后再联合处理的稀疏恢复STAP算法，其本质上仍为单观测矢量情况(Single Measurement Vector, SMV)；文献[9,10]针对稀疏恢复STAP问题进行了深入且系统的研究，一方面研究了基于稀疏滤波器的STAP技术，另一方面针对空时谱稀疏问题重点研究了非参数化迭代稀疏恢复算法，旨在增强算法对正则化参数设置的稳健性和运算量的降低。然而，上述研究均未深入涉及多观测矢量(Multiple Measurement Vector, MMV)联合稀疏问题。

实际上，近年来在脑成像等领域的技术需求，激发了人们基于MMV进行联合稀疏恢复的兴趣[18]，也提出了一些较为有效的算法[18－23]。其中同时正交匹配追踪算法(Simutaneous Orthogonal Matching Pursuit, SOMP)[18－21]是贪婪算法由SMV到MMV的直接拓展，具有较低的运算量，同时在无噪声背景下具有理想的信号恢复性能，是目前最为高效和典型的联合稀疏恢复算法。然而，在实际应用背景下，机载雷达回波信号中除目标和强杂波外不可避免地存在各种噪声，因此，如果简单将SOMP算法引入到STAP技术中，受噪声影响，杂波抑制性能的稳定性将得不到保证。

针对上述问题，本文提出了一种基于杂波子空间的贪婪算法进行联合稀疏恢复，并应用于STAP进行杂波抑制处理。首先，该方法充分利用了多个训练样本中的杂波信息，因此较现有稀疏恢复STAP方法具备更强的信号恢复能力；其次，不同于 SOMP算法中利用剩余杂波矩阵来寻找最大相关原子的策略，该方法采用了剩余杂波子空间投影来寻找最大相关原子，并利用2l范数作为准则来衡量相关性的大小，从而有效回避了杂波矩阵中的噪声分量对稀疏恢复算法的不利影响，同时可高效地寻找到过完备字典中相关性最强的原子。本文最后利用仿真实验验证了所提STAP算法的有效性，并给出了相应结论。

2 机载雷达信号模型及空时谱估计

不考虑距离模糊情况下，机载雷达在某个距离门上的回波信号主要由该距离环上多个离散杂波块的回波叠加而成：

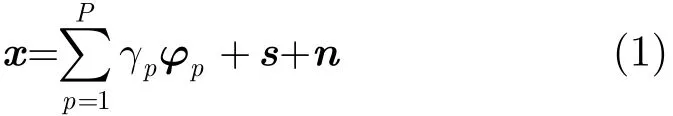
其中p为距离环上杂波块个数，γp为第p个杂波块的散射系数，s为目标信号，n为噪声，ϕp为第p个杂波块对应空时2维导向矢量：

其中, St,p和 Ss,p分别为第p个杂波块对应的时间导向列矢量和空间导向列矢量，且有

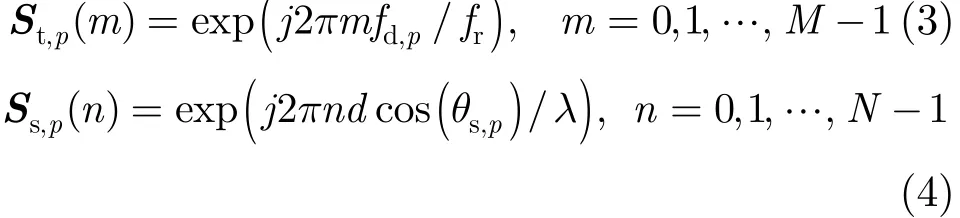
其中，θs,p为第p个杂波块对应的空间锥角，fd,p=2V cos( θs,p)/λ 为第p个杂波块对应多普勒频率，V为载机速度，λ为波长，N为天线阵元数，d为阵元间距，M为相干脉冲数，fr为脉冲重复频率。

由式(1)可知，机载雷达回波信号实际上由不同来向不同多普勒频率的回波信号叠加而成，如果将所有空间频率和多普勒频率均遍历并分别离散化为Ns=ρsN和Nd=ρdM个频率点，且只考虑训练样本中回波信号，则式(1)中信号还可表示为：

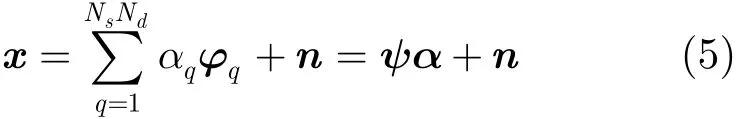
其中，ρs和ρd分别表示离散化程度，在高分辨情况下一般均远大于1, αq为第q个空时网格单元幅度，ϕq为第q个空时网格单元对应的空时2维导向矢量，。由于字典ψ的行数NM远小于列数 NsNd，因此式(5)为病态方程或欠定方程。

即从式(6)中求解稀疏系数矩阵A中的非零元素位置。需要注意的是，本文研究背景为正侧视机载雷达，因此各距离门中杂波分布特性一致，也就是说各距离门中杂波的稀疏结构可认为是相同的。式(6)最终需恢复得到稀疏系数矩阵A中非零行的坐标，即支撑集。

一旦求得A，则可计算出角-多普勒网格上杂波所在位置网格点的幅度，得到杂波空时2维谱的高分辨估计，进而可构造空时自适应权值进行杂波抑制处理。

3 基于子空间正交匹配追踪的STAP方法(Subspace-based OMP, SbOMP)

3.1 算法原理

无噪声情况下，贪婪算法可有效地寻找到支撑集。然而，当观测矢量中含有噪声分量时，现有贪婪算法的稀疏恢复性能会出现较大波动。针对该问题，本文提出了一种基于子空间的贪婪算法进行联合稀疏恢复，并利用其估计空时2维谱构造自适应权值进行杂波抑制处理。该方法对剩余杂波矩阵进行SVD或QR分解，得到剩余杂波子空间，再构造投影矩阵基于l2范数匹配寻找字典中最大相关原子，然后将该原子对应观测矩阵(训练样本)中杂波分量剔除，得到新的剩余杂波矩阵，再返回第1步，不断迭代，直到满足终止条件。在通过联合稀疏恢复得到空时谱中强杂波分量位置后，基于最小二乘可计算出空时谱中杂波分量幅度，进而估计得到杂波协方差矩阵，最终形成空时2维自适应权值进行杂波抑制处理。该方法具体表述如下：

输入：

•NM× L 维训练样本矩阵X。

•稀疏度K。

输出：

•含有K个坐标的集合ΛK。

•NM× NM维投影矩阵 PK。

•NM× L维近似矩阵 ZK。

•NM× L维剩余杂波矩阵 YK。

•NM× NM维杂波协方差矩阵R。

• NM× 1维空时导向矢量W。

程序：

第 1步：初始化剩余杂波矩阵Y0=X，坐标集Λ0=∅和迭代计数k=1。

第2步：计算第k次迭代后剩余杂波矩阵对应的杂波子空间Sk−1以及该子空间对应的投影算子Pk−1。

第3步：通过求解以下最优化问题求解第k次迭代时的坐标kλ

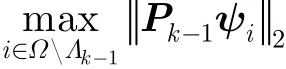
第4步：将第k次迭代时的坐标λk并入坐标集Λ

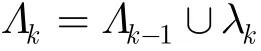
第5步：根据当前坐标集Λk对应字典中的原子计算投影算子 Pk。

第6步：获取新的杂波分量 Zk并根据该分量求得剩余杂波分量 Yk

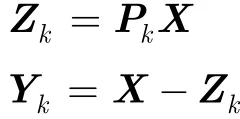
第7步：令 k = k+ 1并返回第2步直到k = K。

第8步：计算杂波协方差矩阵R和空时自适应权值W

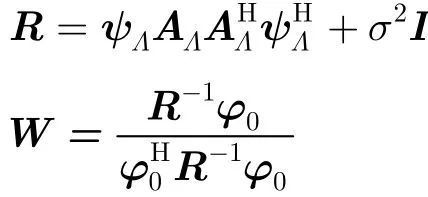
第2步中可通过SVD分解或QR分解算法[24]来计算杂波子空间；第3步中，Ω Λk表示坐标集Ω中除Λk内所含坐标以外的所有坐标的集合；第7步中，迭代次数K与杂波秩有关，根据经验一般选取K为1.5～2倍杂波秩r；第8步中，ψΛ为由ψ中相对于Λ的原子组成的矩阵，AΛ为相对于Λ的稀疏系数矩阵，σ2为噪声方差，目标空时导向矢量ψ0可通过式(2)求取。

3.2 方法分析

已有贪婪算法均利用剩余杂波矩阵与各原子进行相关，依据相关性大小来筛选出与杂波分量最大相关的原子。无噪声情况下，该类方法可高效筛选出r个与杂波相关性最强的原子。然而，存在噪声时受噪声分量影响，该类方法每次迭代并非恰好筛选出与杂波相关的原子，如果迭代次数依旧为r个，则筛选出与杂波相关的原子往往是欠缺的，因此一般迭代次数选取比r稍大来确保所有与杂波相关的原子均被搜索到。同时，与噪声分量相关的部分原子不可避免地也被搜索到，表现为杂波谱上出现部分伪峰，导致杂波抑制性能下降。

本文方法利用剩余杂波子空间构造投影算子来筛选与杂波分量相关的原子，保证了每次与原子进行相关运算的分量为纯杂波分量，因此不会受到噪声等其他因素的干扰。采用该算法每次筛选到的原子必然分布在理想杂波脊上，并随着迭代次数的增加连续性增强。如果迭代次数太少，则体现在杂波谱上较为离散；而如果迭代次数太多，一方面运算量较大；另一方面会导致自动搜索到杂波脊附近相关性相对较强的原子；因此，根据经验值，一般选取迭代次数为1.5～2倍杂波秩r。

4 仿真实验

选取正侧视均匀线阵机载相控阵雷达进行仿真实验，其中载机高度为 9000 m，载机速度为 150 m/s，波长为0.3 m，重频为2000 Hz，主波束俯仰角为3o，天线阵元个数N=8，相干脉冲数M=8，空间频率和多普勒频率超分辨因子ρs和ρd均设为4，待检测距离门为300。共选取4种STAP方法进行对比，包括传统的对角加载协方差求逆法[1,2]，文献[6]中所提稀疏恢复方法，文献[20]中所提联合稀疏恢复算法和本文算法。方便起见，上述4种STAP算法在以下仿真实验中分别简称为 LSMI, SR,SOMP和 SbOMP。需要注意的是，在实验 1～3中杂噪比(Clutter-to-Noise Ratio, CNR)均设定为35 dB，实验1～2中训练样本数均选取为12(依照RMB准则，样本数应不小于30，因此该情况为样本严重不足情况)。

4.1 实验1：杂波空时谱估计对比

本部分主要对比采用不同算法得到的空时谱分布情况，其中LSMI法采用传统的MVDR谱。由图1可以看出，采用稀疏恢复算法估计得到杂波谱的分辨率均显著高于传统 MVDR法。其中，由图1(b)可以看出，采用 SR法得到的谱分布离散化较为严重，且杂波脊附近区域存在伪峰；由图1(c)可以看出，采用SOMP法在杂波脊线上可恢复得到约r个强杂波点，但在其他区域也存在大量离散伪峰，这主要是由于噪声的影响所导致；由图1(d)可以看出，采用所提SbOMP法可沿杂波脊精确恢复出连续的强杂波点，且在其他区域无伪峰出现。

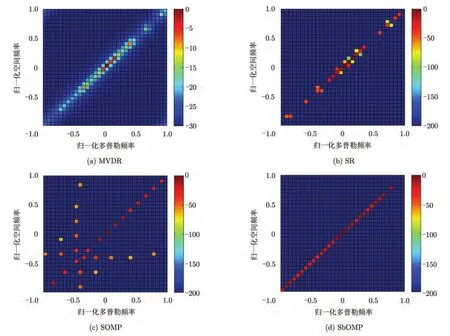
图1 采用不同算法估计空时谱分布情况Fig.1 Space-time spectra corresponding to different estimation algorithm

4.2 实验2：训练样本不足情况下杂波抑制性能对比

本节研究在训练样本不足情况下上述4种算法的杂波抑制性能对比。本文采用改善因子(Improvement Factor, IF)作为基准来衡量杂波抑制性能。其中，改善因子定义为输出信杂噪比(Signal-to-Clutter-plus-Noise Ratio, SCNR)与输入SCNR的比值，具体表述为：

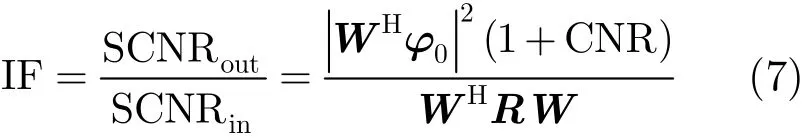
由图2可以得出以下3点结论：一是在训练样本不足的情况下，采用稀疏恢复算法的性能要显著优于传统STAP方法；二是采用联合稀疏恢复算法的主杂波区的抑制性能要显著优于已有稀疏恢复算法，这主要是已有稀疏恢复算法没有充分利用多个训练样本中所蕴含的杂波信息；三是噪声环境下本文所提SbOMB算法的杂波抑制性能要优于经典联合稀疏恢复算法，这验证了所提算法在噪声环境下具有更好的稳健性。

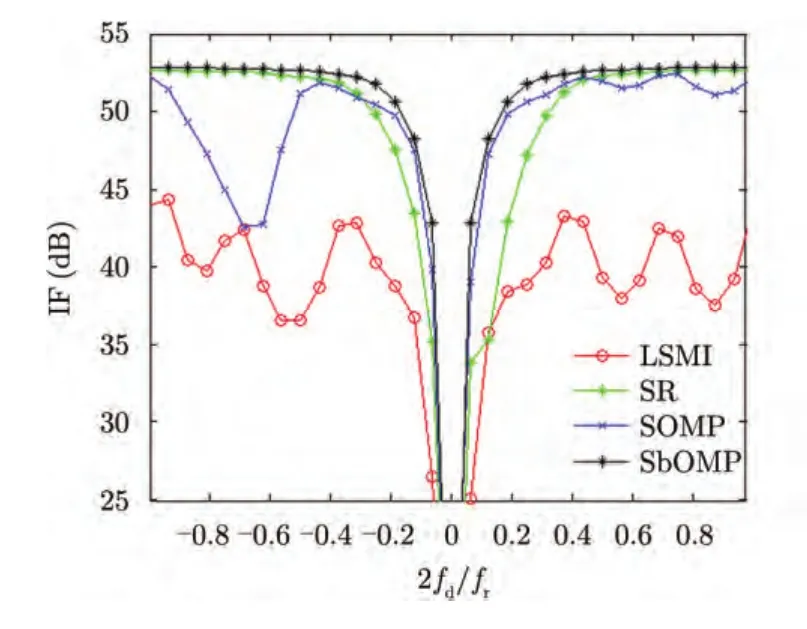
图2 杂波抑制性能对比Fig.2 Clutter suppression performance comparison

4.3 实验3：不同输入CNR情况下杂波抑制性能对比

本节主要研究在不同噪声背景下，所提基于子空间的联合稀疏恢复算法与经典联合稀疏恢复算法的杂波抑制性能对比。其中，Known Cov.算法为已知杂波协方差矩阵下协方差矩阵求逆方法，相应STAP处理器为最优处理器，提供算法性能上限，以方便对比。本实验中，采用各多普勒通道对应改善因子的平均值，即平均改善因子(Average Improvement Factor, AIF)作为标准来衡量杂波抑制性能。共进行50次蒙特卡诺仿真。由图3可以看出，在CNR低于35 dB的情况下，所提SbOMP算法的杂波抑制性能比SOMP算法可改善约3～10 dB；而在噪声相对较弱(杂噪比较大)情况下，相较于SOMP算法，SbOMP算法的杂波抑制性能也有约1 dB的改善。

5 结论

本文将经典联合稀疏恢复算法应用于机载雷达STAP处理，并针对其所存在的问题提出了一种基于子空间的联合稀疏恢复STAP方法。研究表明，相比于已有稀疏恢复算法，采用联合稀疏恢复STAP算法后，对主瓣杂波的抑制性能有了显著提升；同时，所提基于子空间联合稀疏恢复 STAP算法解决了经典联合稀疏恢复算法在噪声背景下性能下降的问题。实际上，本文算法由于涉及子空间处理，因此运算量较经典联合稀疏恢复算法有所提升；此外，在极少训练样本情况下，本文算法的旁瓣抑制性能并不理想，下一步重点针对这些问题开展进一步研究。

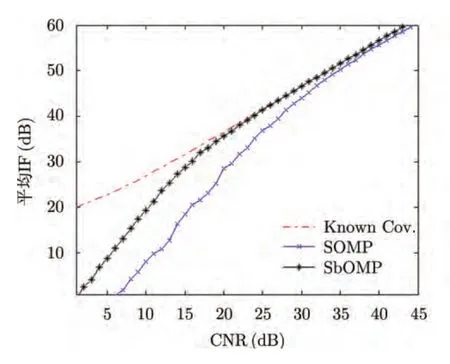
图3 不同输入CNR情况下平均IF对比Fig.3 Average IF comparison of different input CNRs

[1]Klemm R.Principles of Space-Time Adaptive Processing[M].London: Institute of Electical Engineering, 2006.

[2]王永良, 彭应宁.空时自适应信号处理[M].北京: 清华大学出版社, 2000.Wang Y L and Peng Y N.Space-Time Adaptive Processing[M].Beijing: Tsinghua University Press, 2000.

[3]Reed I S and Mallett J D.Rapid convergence rate in adaptive arrays[J].IEEE Transactions on Aerospace and Electronics Systems, 1974, 10(6): 853-863.

[4]Selesnick I W, Pillai S U, Li K Y, et al..Angle-Doppler processing using sparse regularization[C]. IEEE International Conference on in Acoustics, Speech and Signal Processing, Dallas, TX, USA, 2010: 2750-2753.

[5]Li J, Zhu X, Stoica P, et al..Iterative space-time adaptive processing[C].IEEE Digital Signal Processing Workshop,Marco Island, FL, 2009: 440-445.

[6]Sun K, Zhang H, Li G, et al..A novel STAP algorithm using sparse recovery technique[C].IEEE International Conference on Geoscience & Remote Sensing Symposium, Cape Town,2009: 336-339.

[7]Sun K, Meng H, Wang Y, et al..Direct data domain STAP using sparse representation of clutter spectrum[J].Signal Processing, 2011, 91(9): 2222-2236.

[8]Sun K, Meng H, Lapierre F D, et al..Registration-based compensation using sparse representation in conformal-array STAP[J].Signal Processing, 2011, 91(10): 2268-2276.

[9]Yang Z C, de Lamare R C, and Li X.l1-Regularized STAP algorithms with a generalized sidelobe canceler architecture for airborne radar[J].IE EE Transactions on Signal Processing, 2012, 60(2): 674-686.

[10]Yang Z C, de Lamare R C, and Li X.Sparsity-aware Space-Time Adaptive Processing algorithms with l1-norm regularization for airborne radar[J].IET Signal Processing,2012, 6(5): 413-423.

[11]Chen S, Donoho D, and Saunders M.Atomic decomposition by basis pursuit[J].SIAM Review, 2001, 43(1): 129-159.

[12]Tropp J A.Just relax: convex programming methods for identifying sparse signals in noise[J].IEEE Transactions on Information Theory, 2006, 53(3): 1030-1051.

[13]Wright S J, Nowak R D, and Figueiredo M A T.Sparse reconstruction by separable approximation[J].IEEE Transactions on Signal Processing, 2009, 57(7): 2479-2493.

[14]Tropp J A.Greed is good: algorithmic results for sparse approximation[J].IEE E Transactions on Information Theory, 2004, 50(10): 2231-2242.

[15]Tropp J A and Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.

[16]Needell D and Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J].IEEE Journal of Selected Topics on Signal Processing, 2009, 4(2): 310-316.

[17]Gorodnitsky I F and Rao B D.Sparse signal reconstruction from limited data using FOCUSS: a re-weighted minimum norm algorithm[J].IEEE Transactions on Signal Processing,1997, 45(3): 600-616.

[18]Cotter S, Rao B, Engan K, et al..Sparse solutions to linear inverse problems with multiple measurement vectors[J].IEEE Transactions on Signal Processing, 2005, 53(7):2477-2488.

[19]Tropp J, Gilbert A, and Strauss M.Algorithms for simultaneous sparse approximation.Part I: Greedy pursuit[J].Signal Processing, 2006, 86(3): 572-588.

[20]Chen J and Huo X.Theoretical results on sparse representations of multiple-measurement vectors[J].IEEE Transactions on Signal Processing, 2006, 54(12): 4634-4643.

[21]Gribonval R, Rauhut R, Schnass K, et al..Atomsof all channels, unite! average case analysis of multi-channel sparse recovery using greedy algorithms[J].Journal of Fourier Analysis Applications, 2008, 14(5/6): 655-687.

[22]Tropp J A.Algorithms for simultaneous sparse approximation.Part II: Convex relaxation[J].Signal Processing, 2006, 86(3): 589-602.

[23]Wipf D P and Rao B D.An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J].IEEE Transactions on Signal Processing, 2007, 55(7):3704-3716.

[24]Goldstein J S and Reed I S.Theory of partially adaptive radar[J].IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(4): 1309-1325.