高维分类型数据加权子空间聚类算法

孙浩军，闪光辉，高玉龙，袁 婷，吴云霞

汕头大学 工学院，广东 汕头 515063

高维分类型数据加权子空间聚类算法

孙浩军，闪光辉，高玉龙，袁 婷，吴云霞

汕头大学 工学院，广东 汕头 515063

聚类就是将物理或抽象的数据集合分成相似的对象类的过程，每一个类都是一个彼此相似的对象的集合，每一个对象与属于同一个类中的对象彼此相似，而与其他类中的对象相异[1]；聚类是理解数据库中数据结构的一种重要手段，它在机器学习、模式识别、数据挖掘、信息检索等方面都扮演着重要角色[2]，研究者们已经提出多种数据聚类算法[3-5]，然而在现实生活中，好多数据都拥有很高的维度，由于低维数据与高维数据在很多地方都表现出很大的不同，比如高维数据的稀疏型和“维度效应”[6]等，当用传统的方法对高维数据聚类时，算法的有效性就大为降低，这也就成为目前聚类研究中的难题之一。

高维数据中往往有许多无关的属性或者是相关性特别小的属性，它们对聚类过程带来的噪声信息往往比带来的有用信息还要多。在高维数据聚类中，尤其是在高维稀疏型数据集中，较密集的簇主要集中在一些低维子空间中，并且不同的簇往往与不同的子空间相关联[7]，子空间聚类算法[8]的提出在一定程度上解决了这一问题。

根据加权方式的不同，子空间聚类可以分为软子空间（soft subspace）和硬子空间（hard subspace）聚类两种[9]。软子空间又可称为加权子空间，它给子空间的维度赋予[0，1]的权值，表示该维度与该簇的关联程度；而硬子空间则是把子空间的维度同等看待，认为它们与该簇的关联程度相同。现有的聚类算法着重于划分的优化而忽略了子空间的优化或者是采用一个全局参数硬性的选取子空间，如 EWKM[9]的 γ、FKWM[10]的 β、δ等，这些在实际应用中都是很难确定的。

针对连续性数据，人们已经研究出K-means[4]、PAM[5]等经典算法。但是，用于连续性数据的聚类算法对于分类型数据数据却显得无能无力，因为对于连续性数据，基于距离的几何性质可以作为一个标准[11]，但是分类数据的数据值是离散的，基于几何性质的距离函数不再适用。对于分类型数据的相似度，现有的算法一般采用相异度作为分类型数据之间的距离度量，如：Dice/Jaccard系数和汉明距离等，但是使用它们有明显的缺陷[12]，因为分类型数据属性的值域十分狭小，即使低维的分类型数据也会经常出现“维度效应”问题，它们的相异度十分趋向于同一个值，在高维数据中更是如此。

针对这些问题，提出一种加权子空间聚类算法（Algorithm for Weighted Subspace Clustering，AWSC）。AWSC算法基于经典的蚁群聚类算法的聚类过程，采用层次聚类中凝聚聚类的思想进行聚类。在聚类过程中，采用基于子空间的特征向量加权计算两个簇的相似度，减少了“维度效应”等因素的影响。

1 相关知识和理论基础

1.1 信息熵

熵，最初作为一个热力学概念，用来度量热量的退化或进化。熵是系统无序程度的度量，熵越大，无序性越高，变化可能性越大，香农在信息论中引入熵的概念用来度量信息系统结构的不确定性。依据熵值计算权重[13]已有很多算法，本算法就是基于信息熵理论的基本原理来计算权重的。设有一个信源 X，其概率空间为xi，它们满足：

其信息熵计算公式为：

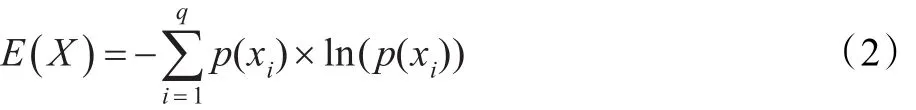
从上式可以看出，当X中某一个变量出现概率较大时，则X的信息熵就较小，而当X中的变量出现越均匀，X的信息熵就越大。X的信息熵在一定程度上就代表了X中变量的易变程度或者说是紧凑程度，这样信息熵就可以用在聚类过程中的子空间的搜索。

1.2 聚类的特征子空间

在高维数据聚类中，尤其是在高维稀疏型数据中，子空间的搜索是至关重要的。在搜索子空间时，子空间数据应尽可能地紧凑，噪声空间的数据应尽可能地凌乱，然而，怎样在两者之间找到一个平衡是一个难题，现有的算法很多是以一个固定的全局参数以信息熵为标准对子空间进行选择，这样的算法在实际应用中会有很大的限制。针对这一问题，以信息熵为基础，找到一个自适应函数 f(e)用于簇的特征子空间的搜索。

首先，应计算出簇的所有维的信息熵，然后，对信息熵按下式进行预处理，使std(i)∈[0，1]，以方便计算。

entropy(i)、min、max分别代表第i维的信息熵值、簇的最小信息熵值和最大信息熵值，std(i)表示第i维的预处理之后的信息熵，称它为标准信息熵。

其次，按自适应函数 f(e)计算出该簇的特征子空间，所求出的子空间应使 f(e)取得最小值。该函数既考虑了子空间的数据的紧凑度，又考虑了噪声空间的凌乱程度，以达到子空间搜索的合理化。

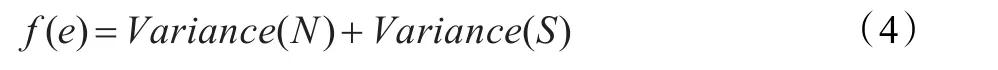
这里N、S分别是该簇的噪声子空间和特征子空间；Variance(N)、Variance(S)分别为噪声子空间和特征子空间的标准信息熵的方差，定义如下：

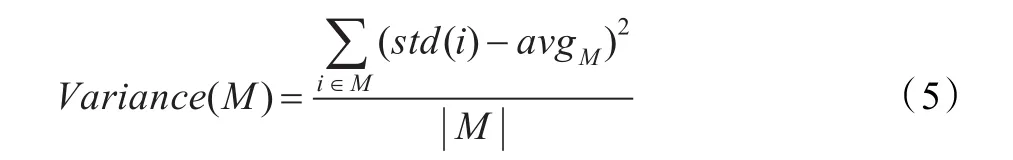
其中| M |为子空间M的维数，avgM为子空间M上维的标准信息熵的平均值。

由函数 f(e)求出的特征子空间能代表所属簇的属性特征。子空间的特征向量[14]就是在子空间所在的维上的特征值所组成的向量，在分类数据中维的特征值就是在簇中该维上出现次数最多的值，由特征子空间中维的特征值组成的特征向量就能代表所属簇的特征。

1.3 子空间权值

在特征子空间中，虽然该子空间中维和簇的关联程度相对来说已经很高，但是，不同的维与簇的关联程度不可能完全相同，维的信息熵恰恰说明了这一点。但是进行子空间权重的分配时，如果仅仅依据信息熵进行权重的分配是不合理的，比如：两个簇A、B在同一维上信息熵A的较大、B的较小，如果B中元素个数远多于A，在聚类过程中B对聚类结果的影响应大于A，那么就应该赋予该维较大的权重，反之相反。因此，将子空间的权重设计为由两个簇的子空间的信息熵及簇的大小确定。先分别求出两个簇的子空间，然后在两个子空间的并集上计算着两个簇合并时子空间维的权重。比如：簇 A的子空间为（2，3，4，5），簇 B 的为（3，4，5，7），那么A、B 两个簇的子空间的并集就是（2，3，4，5，7）。然后求出子空间的并集（2，3，4，5，7）每一维的权重，以计算 A、B两簇的相似度。那么，第 j维的权重就可以表示为：

式中，X为两簇的子空间的并集；|A|、|B|、| X|分别为A、B两簇的大小和两簇子空间并集的大小；std(a，j)、std(b，j)分别为 A、B子空间并集上第 j维的标准化熵值；其中，α是为了让维的熵值为0的情况下使该式有意义而加入的一个松弛量，为了让权值的计算尽可能地依据熵值和簇的大小，不让α对权值的计算产生大的影响，令α为0.000 1；β、γ是两个参数，它们决定簇的大小和信息熵值对权值的影响，较大的β意味着信息熵对权重的影响较小；较大的γ则意味着簇的大小对权重的影响就越大；反之均相反。采用类似熵权法[13]以熵求权的算法中的权值的计算方式，直接简单地令 β、γ为1。这样子空间权重的分配就显得更加合理，因为一维权值的大小与合并前两簇的子空间的维的信息熵的大小和簇的大小都直接相关；熵越小，权值应越大；簇越大，权值也应越大；所以把计算权重的公式定为以上形式，这样求出的权值能更好地用于计算簇的相似度。

1.4 相似度

相似度描述的是两个物体的相似程度，在聚类中，相似度在很大程度上可以说是两个数据属于同一个类的概率，分类数据相似度的度量不同于连续型数据的相似度的几何度量方式，传统的欧氏距离等基于几何性质的距离方式对分类数据已经失效。

传统的用于分类数据的相似度的度量方式如下：假设有同属于一个数据集 X的两个分类型数据，X1(x11，x12，…，x1q)、X2(x21，x22，…，x2q)，它 们 的 相 似 度 可 以 定义为：

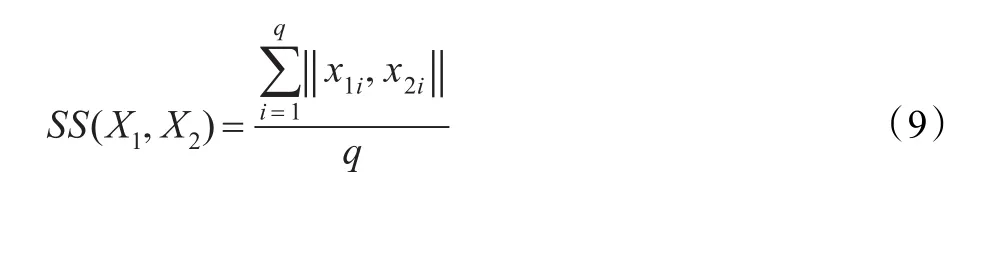
这里q为数据集 X的维数，x1i、x2i为 X1、X2在第i维的值。

受CLUC[15]算法的影响，把上式加以扩展得到以下几个相似度的计量方式：

一条分类型数据和一个分类型簇的相似度：

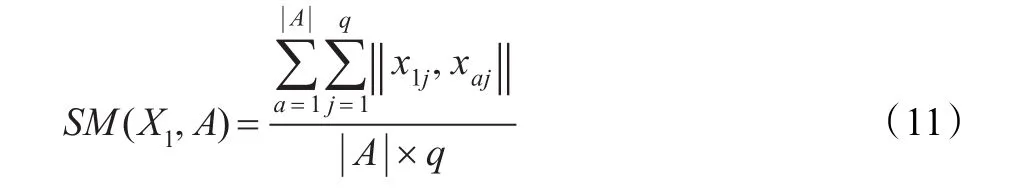
如果再把此式扩展一下就能得到两个分类型数据簇的相似度。

假如现有两个分类型数据的簇A、B，它们基于子空间并集的相似度定义为：

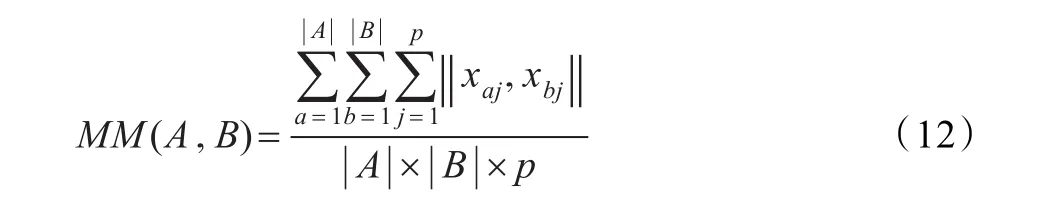
如果再对A、B的子空间的并集加权处理，那么它们基于子空间的加权相似度可定义为：

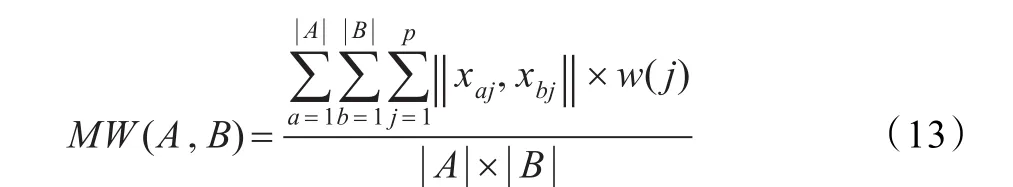
如果再对A、B取子空间的特征向量，那么它们基于子空间特征向量的加权相似度可定义为：

这里，|A|、|B |为簇A、B的元素个数，xaj、xbj分别为 A中第a、第b个数据元素在第 j维的值，q为簇 A特征子空间的维数，p为A、B两簇子空间并集的维数，w(j)为A、B子空间的并集中第 j维的权重，vai表示簇 A特征向量中第i维的值。

这一系列相似度的计量方法（式（11）～（14）），其实也是信息熵的一个扩展。但是它们克服了信息熵的一个缺点，按信息熵进行矩阵的相似度计算时，如果两个矩阵大小相差很大，就会出现意外情况，达不到理想的聚类效果。提出的簇的相似度的计算方式克服了这一缺点，该算法在计算矩阵的相似度时与矩阵的大小无关。

2 算法AWSC

本文的算法大致分为两步：首先，数据的预处理，进行数据的初始化。然后，对初始化后的数据进行聚类。

2.1 数据的预处理

本算法数据的预处理是为了降低算法复杂性，减少对计算机硬件的要求，减少噪声数据对聚类的影响。

初始化时，采用一个参数 init_rate（0～1），按式（9）、（11）将数据集做初始的划分。采用凝聚的概念进行数据集的初始化。首先，遍历原数据集，当取第一个元素时，把它当做一个初始簇，然后，遍历其他元素时，通过式（9）或（11）计算它与已有簇的相似度，当它在所有簇中的相似度都小于阈值init_rate时，就把该元素存入一个新簇中，簇的个数增1，当有相似度大于阈值时，就把该元素存入相似度最大的簇中，直至遍历结束。

2.2 聚类阶段

在数据的预处理之后，初始簇的个数远小于远数据集中数据个数，接下来的阶段就是对初始簇按最大相似度进行合并，直到达到预定类的个数。

2.2.1 子空间的确定及相似度的计算

首先，由式（4）找到初始簇的子空间，找出每个初始簇的特征子空间的特征向量。

然后，以特征子空间的特征向量为基础计算初始簇之间的相似度。在计算时，首先由式（7）计算两簇的子空间权重的分配，由两个簇的子空间特征向量、簇的大小以及子空间权重经式（14）计算两簇的相似度，从而得到由所有簇对的相似度组成的相似度矩阵。

2.2.2 初始簇的合并

根据相似度矩阵，找到拥具最大相似度的一对簇进行合并；如果相似矩阵有多对簇具有最大相似度则由式（13）找出具有较大值的两个簇进行合并；合并之后，如果初始簇的个数等于预定类个数K，则算法结束；否则，重新计算簇的子空间及相似度矩阵，再进行合并，直到初始簇的个数达到预定类个数K。

2.3 算法伪代码

伪代码如下：

算法AWSC

输入：数据集D；类的个数K；阈值init_rate

输出：C 个子集的集合C{c1，c2，…，ck}

初始化：根据式（9）、（11）及参数 init_rate把数据初始化为clusters个簇

Repeat

（1）由式（4）计算每个簇的子空间及其特征向量；

（2）由式（4）、（7）计算子空间权重；

（3）由式（14）得到相似度矩阵；

（4）结合式（13）进行簇的合并；

Until clusters=K

3 实验仿真及结果分析

实验仿真采用的是UCI机器学习网站[16]上的数据集，并与其他算法[17-21]仿真结果进行分析比较；聚类结果的分析主要依靠聚类的正确率。

3.1 评价指标

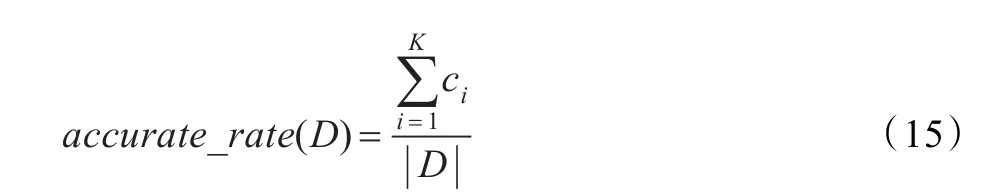
聚类正确率的计算公式如下：其中，K为该数据集的真实的类的个数，Ci为第i个类聚类正确的数据个数，|D|为该数据集的元素个数。

3.2 数据实验

在这里选用了Congressional Voting Records Data Set（Votes）、Zoo Data Set（Zoo）以及Soybean Data Set（Soybean）3个典型的真实分类型数据集。

3.2.1 数据描述

Votes是435×17的数据集，第一维为类标识，数据分为2类，一类是民主党包含267个数据，另一类是共和党包含168个数据。

Soybean是47×36的数据集，第一维为类标识，数据分为 D1、D2、D3、D44类，其中 D1、D2、D3、D4的数据量分别为10、10、10、17。

Zoo是101×17的数据集，第一维为类标识，数据集供分为 7类，类包含的数据量分别为41、20、5、13、4、8、10。三个数据集的信息如表1所示。其中Votes中有一些数据的属性值缺失，本算法中对其以“？”作为标示。

表1 数据集基本信息

3.2.2 实验结果及对比

其他几个算法[13，18-21]在这几个数据集上准确率如表2所示。其中，AWSC的结果是在init_rate=0.85的情况下产生的；CEVE、RDCE、RRCE算法的结果是取得10次计算中最好结果，“*”为相关算法中没有此数据集的验证，默认效果是不太理想，在图1中为了图形的完整性，以其他算法的平均值作为补充。

表2 各算法在数据集上的正确率

从以上各表可以看出，AWSC算法明显优于其他算法，为了更直观地对比各个算法的效果，将各个算法的实验结果用直方图的形式描述出来，如图1所示。

由图1可以看出，AWSC算法明显优于其他算法，充分地体现了AWSC算法的有效性和优越性。这是因为本文算法设计的合理性。为更好地说明本算法的合理性，特对不同参数下的各数据集的正确率进行分析，具体结果如图2。

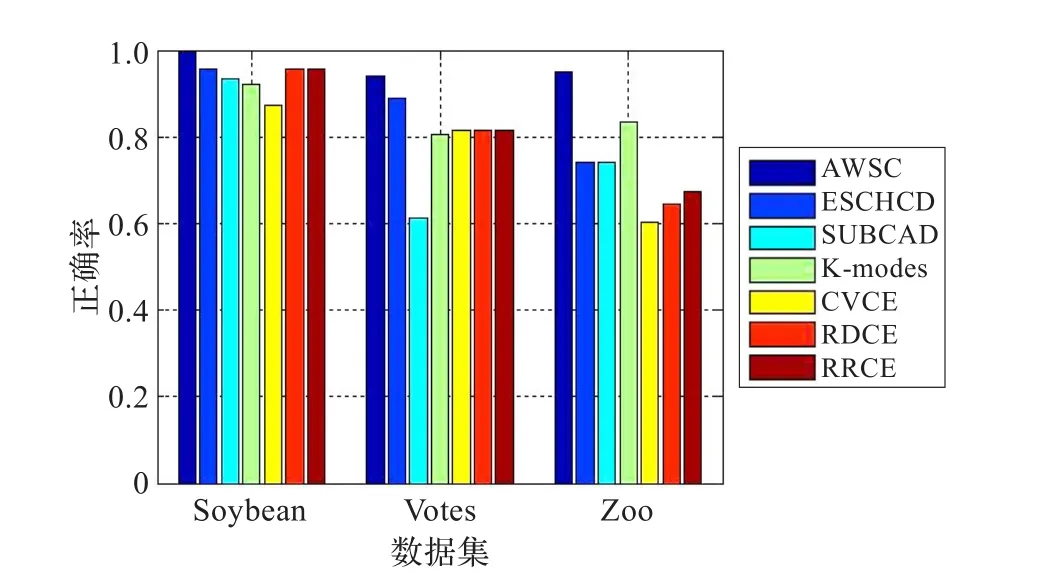
图1 各算法在不同数据集的准确率

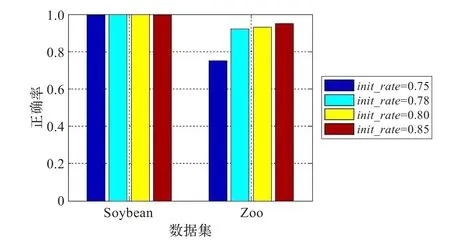
图2 Soybean、Zoo在不同参数下的准确率

Soybean、Zoo两个数据集有一定的特殊性，所以选择这两个数据集作为分析对象。就像3.2.1节描述的那样，这两个数据集在数据的分布上有较大的差异，很具有代表性。Soybean数据集簇的大小分布比较均匀，而且经实验发现，Soybean数据集中的四个簇紧凑性较好；而Zoo数据集的簇的大小的分布就很不均匀，较大的簇的大小达到41，较小的却只有4，不仅如此，在这四个数据里，只有3个数据是比较紧凑的，而另一个数据离另外3个数据比较“远”。

由图2可以看出，Zoo在不同的参数下聚类效果有明显的差异。对Zoo数据集，因为数据簇的大小分布不均匀，所以看到init_rate较小的时候，聚类效果并不好，这是因为在这种情况下，就会把更多的数据在数据的初始化时凝聚到一块，这样较大簇的异常数据和较小簇的数据就有可能聚到一块，导致聚类效果的降低；而当init_rate取较大值时，这时只有相似性较大的数据初始化时聚到一块，这时就能取得较好的聚类效果。所有的这些在Soybean数据集的聚类效果图中可以明显地感受到，从图2可以看出，Soybean在图中列出的参数情况下大部分都能取得很好的聚类效果，就像最初分析的那样，Soybean数据集簇的大小分布比较均匀、簇内紧凑度较好的缘故。其实，它们在其他参数下也能取得较好的聚类效果，图中没有一一列出。

AWSC算法的性能来源于它的自适应性以及权重分配的合理性。每合并两个簇后，AWSC算法都重新搜索新合并成簇的子空间，这样就能更准确地搜索出每个簇的子空间；权重分配时考虑簇的大小对权重分配的影响，从而获得较好的聚类效果。

4 结论及展望

提出了一种加权子空间聚类算法。它利用信息熵和方差去搜索子空间，找到了一个自适应的约束方程，充分地考虑了子空间和噪声空间的影响，使子空间的搜索更加合理；在分配子空间权重时，考虑子空间信息熵和簇的大小的影响，由此推导出了新的子空间维的权重计算方式。与其他算法相比，AWSC算法权重的分配更加合理，子空间的搜索也更加合理，大幅提高了聚类精度和聚类结果的稳定性。下一步的工作重点是减少参数的个数，进一步提高聚类算法的适应性。

[1]Han Jiawei，Kamber M.数据挖掘概念与技术[M].范明，孟晓峰，译.北京：机械工业出版社，2008：16-17，30-31，251-252.

[2]Iam-On N，Boongoen T，Garrett S，et al.A link-based cluster ensemble approach for categorical data clustering[J]. IEEE Knowledge and Data Engineering，2012，24（3）：413-425.

[3]Berkhin P.Survey of clustering data mining techniques[M]// Grouping multidimensional data：recent advances in clustering.Berlin：Springer-Verlag，2006：25-71.

[4]Macqueen J.Some methods for classification and analysis of multivariate observations[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability.Berkeley：University of California Press，1967：281-297.

[5]Kaufman L，Rousseeuw P J.Finding groups in data：an introduction to cluster analysis[M].Hoboken：John Wiley& Sons Inc，1990：68-72.

[6]Parsons L，Haque E，Liu H.Subspace clustering for high dimensionaldata：areview[J].ACM SIGKDD Explorations Newsletter，2004，6（1）：90-105.

[7]Zaki M J，Peters M，Assent I，et al.CLICKS：an effective algorithm for mining subspace clusters in categorical datasets[C]//Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining，2005：736-742.

[8]Tan S，Cheng X，Ghanem M，et al.A novel refinement approach for text categorization[C]//Proceedings of the ACM 14th Conference on Information and Knowledge Management，2005：469-476.

[9]Jing L，Ng M K，Huang J Z.An entropy weighting k-means algorithm forsubspace clustering ofhigh-dimensional sparese data[J].IEEE Trans on Knowledge and Data Engineering，2007，19（8）：1026-1041.

[10]Huang J Z，Ng M K，Rong H，et al.Automated variable weighting in k-means type clustering[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2005，27（5）：657-668.

[11]Karypis G，Han E H，Kumar V.Chameleon：hierarchial clustering dynamic modeling[J].IEEE Journals&Magazines，1999，32（8）：68-75.

[12]孙浩军，杜育林，姜大志.基于信息熵的高维分类型数据子空间聚类算法[J].山东大学学报：自然科学版，2011，45（5）：37-45.

[13]陈孝新，熵权法在股票市场的应用[J].商业研究，2004（16）：139-144.

[14]Zhang P，Wang X，Song P X.Clustering categorical data based on distance vectors[J].The J Am Statistical Assoc，2006，101（473）：355-367.

[15]Nemalhabib A，Shiri N.CLUC：a natural clustering algorithm for categorical[J].ACM，2006：23-27.

[16]UCI data base[EB/OL].[2012-12-19].http：//archive.ics.uci. edu/ml/datasets.html.

[17]He Zengyou，Xu Xiaofei，Deng Shengchun.A cluster ensemblemethod forclustering categoricaldata[J].Information Fusion，2005，6（2）：143-151.

[18]李桃迎，陈燕，张金松，等.一种面向分类属性数据的聚类融合算法研究[J].计算机应用研究，2011，28（5）：1671-1673.

[19]马海峰，刘宇熹.基于相关随机子空间的分类数据聚类集成[J].计算机应用研究，2012.

[20]San O M，Huynh V，Nakamori Y.An alternative extension of the k-means algorithm for clustering categorical data[J].International Journal of Applied Mathematics and Computer Science，2004，14（2）：241-247.

[21]Gan G，Wu J.Subspace cluatering for high dimensional categorical data[J].ACM SIGKDD Explorations Newsletter，2004，6（2）：87-94.

SUN Haojun,SHAN Guanghui,GAO Yulong,YUAN Ting,WU Yunxia

College of Engineering,Shantou University,Shantou,Guangdong 515063,China

Subspace clustering is a kind of effective strategy to high-dimensional data clustering,the principle of subspace clustering is as well as possible keeping original data information,meanwhile as small as possible using subspace to data clustering.Based on the studying of the existing soft subspace clustering,it proposes a new algorithm for subspace searching.The algorithm combines with the size of cluster and information entropy,defines a new subspace dimensional weight distribution mode,and then uses the feature vector of cluster subspace to measure the similarity of two clusters.It uses the idea of agglomerative hierarchical clustering in hierarchical clustering to data clustering,which overcoming the shortcomings of using information entropy or traditional similarity separately.Through the test in the Zoo,Votes,Soybean three typical categorical data set to find out that compared with other algorithms,the proposed algorithm not only can improve the accuracy of clustering,but also has the very high stability.

high-dimensional data;clustering;subspace;information entropy;hierarchical clustering

子空间聚类是高维数据聚类的一种有效手段，子空间聚类的原理就是在最大限度地保留原始数据信息的同时用尽可能小的子空间对数据聚类。在研究了现有的子空间聚类的基础上，引入了一种新的子空间的搜索方式，它结合簇类大小和信息熵计算子空间维的权重，进一步用子空间的特征向量计算簇类的相似度。该算法采用类似层次聚类中凝聚层次聚类的思想进行聚类，克服了单用信息熵或传统相似度的缺点。通过在Zoo、Votes、Soybean三个典型分类型数据集上进行测试发现：与其他算法相比，该算法不仅提高了聚类精度，而且具有很高的稳定性。

高维数据；聚类；子空间；信息熵；层次聚类

A

TP301

10.3778/j.issn.1002-8331.1301-0121

SUN Haojun,SHAN Guanghui,GAO Yulong,et al.Algorithm for high-dimensional categorical data weighted subspace clustering.Computer Engineering and Applications,2014,50（23）：131-135.

国家自然科学基金（No.61170130）。

孙浩军（1963—），男，教授，研究领域为模式识别、数据挖掘等；闪光辉（1986—），男，硕士研究生，研究领域为数据挖掘技术与应用；高玉龙（1988—），男，硕士研究生，研究领域为数据挖掘技术与应用；袁婷（1988—），女，硕士研究生，研究领域为数据挖掘技术与应用；吴云霞（1988—），女，硕士研究生，研究领域为数据挖掘技术与应用。

E-mail：haojunsun@stu.edu.cn

2013-01-14

2013-03-29

1002-8331（2014）23-0131-05

CNKI网络优先出版：2013-07-15,http://www.cnki.net/kcms/detail/11.2127.TP.20130715.0936.002.html