分数阶非线性方程近似解析解的新解法

董立华，刘艳芹

德州学院 数学科学学院，山东 德州 253023

分数阶非线性方程近似解析解的新解法

董立华，刘艳芹

德州学院 数学科学学院，山东 德州 253023

1 引言

分数阶非线性方程已广泛地应用到黏弹性流体、扩散过程、生物力学、固态物理等很多领域[1-4]。伴随着非线性科学的发展，涌现出了很多求解分数阶非线性方程的解析和数值方法[5-7]。而分数阶偏微分方程的解析解难以推导，而现有的解析近似方法又有其自身的缺点[8-9]，需要计算复杂的Adomian多项式和Lagrange乘子等，近年来很多学者对这些方法做了改进[10-11]。Wu[12-13]将Laplace变换和变分迭代法相结合，克服了分数阶Lagrange乘子难以计算的困难。在前人研究的基础上本文提出一种新的修正方法，将变分迭代法、同伦扰动法和Laplace变换相结合，并将该方法应用于分数阶非线性发展方程的求解，其中利用Laplace变换推导分数阶的Lagrange乘子，而He的多项式则用来处理方程中出现的非线性项，该方法简单有效。

2 方法简介

考虑如下的时间分数阶方程：

首先根据修正的变分迭代法[12-13]，方程（1）和（2）两边作Laplace变换并得到方程的迭代格式为：考虑L[R[un(x，t)]+N[un(x，t)]]为变分项，可得到Lagrange乘子为 λ(s)=-1/sα，方程（3）两边再作逆Laplace变换 L-1得到：

u0(x，t)为方程（1）的初始迭代值，包含了初始值和源汇项的信息：

齐次方程非线性项的处理。根据同伦扰动法假设方程的解可以表示为p的幂级数：

3 时间分数阶耦合的MKdV方程及其近似解

考察如下的求解时间分数阶耦合的MKdV方程[15]。

γ是任意常数，当α=1时精确解为：

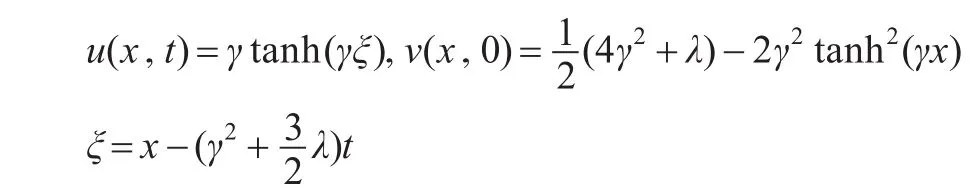
这里 t＞0，0＜α≤1，初始条件为：方程（5）～（6）两边作Laplace变换得到如下迭代格式：

u0，v0是式（5）和（6）的初始迭代值，取 u0=u(x，0)，v0= v(x，0)，应用上述修正的新方法得到：

图1 方程（5）～（6）的精确解 u(x，t)当 λ=1，γ=0.1

图3 方程（5）～（6）的二阶近似解 u0+u1当 α=λ=1，γ=0.1

图4 方程（5）～（6）的二阶近似解 v0+v1当 α=λ=1，γ=0.1

图 1和图 2分别表示方程（5）～（6）精确解 u(x，t)，v(x，t)的图像。图3和图4分别表示方程（5）～（6）二级近似解的图像当α=1。从图像可以看出这种新方法具有较高的精确度，而且不需要复杂的计算。

4 结果和讨论

这种新的方法结合了变分迭代法、同伦分析法和Laplace变换三种处理方法的优点，便于简单计算Lagrange乘子和方便处理非线性项。实例证明该方法可以用于其他分数阶的非线性方程。

[1]Podlubny I.Fractional differential equations：an introduction to fractional derivatives，fractional differential equations，to methods of their solution and some of their applications[M].New York：Academic Press，1999：69-265.

[2]Ma J H，Liu Y Q.Exact solution for a generalized nonlinear fractional Fokker-Planck equation[J].Nonlinear Analysis：Real World Applications，2010，11（1）：515-521.

[3]Metzler R，Klafter J.The random walks guide to anomalous diffusion：a fractional dynamics approach[J].Physics Reports，2000，339（1）：1-77.

[4]Yildirim A.Application of the homotopy perturbation method forthe Fokker-Planck equation[J].Communications in Numerical Methods in Engineering，2010，26（9）：1144-1154.

[5]He J H.Homotopy perturbation method：a new nonlinear analytical technique[J].Applied Mathematics and Computation，2003，135（1）：73-79.

[6]Gupta P K，Yildirim A，Rai K N.Application of He’s homotopy perturbation method for multi-dimensional fractional Helmholtz equation[J].Int J Num Meth Heat& Fl Flow，2012，22（4）：424-435.

[7]Liu Y Q，Ma J H.Exact solutions of a generalized multifractional nonlinear diffusion equation in radial symmetry[J]. Communications in Theoretical Physics，2009，52（5）：857-861.

[8]Liu Y Q.Approximate solutions of fractional nonlinear equations using homotopy perturbation transformation method[J].Abstract and Applied Analysis，2012.

[9]Liu Y Q.Study on space-time fractional nonlinear biologicalequation in radialsymmetry[J].MathematicalProblems in Engineering，2013.

[10]Liu Y Q.Variational homotopy perturbation method for solving fractional initial boundary value problems[J]. Abstract and Applied Analysis，2012.

[11]Guo S M，Mei L Q，Li Y.Fractional variational homotopy perturbation iteration method and its application to a fractional diffusion equation[J].Applied Mathematics and Computation，2013，219（11）：5909-5917.

[12]Wu G C，Baleanu D.Vatiational iteration method for fractional calculus-a universal approach by Laplace transform[J].Advances in Difference Equations，2013，18：1-9.

[13]Wu G C.Laplace transform overcoming principle drawbacks in application of the variation iteration method to fractional heat equations[J].Thermal Science，2012，16（4）：1257-1261.

[14]Ghorbani A.Beyond Adomian polynomials：He polynomials[J].Chaos Solitons&Fractals，2009，39（3）：1486-1492.

[15]Liu J C，Hong L.Approximate analytic solutions of timefractionalHirota-Satsumacoupled KdV equation and coupled MKdV equation[J].Abstract and Applied Analysis，2013.

DONG Lihua,LIU Yanqin

School of Mathematical Sciences,Dezhou University,Dezhou,Shandong 253023,China

A novel method which is based on variational iteration method,Laplace transform and homotopy perturbation method is proposed,and this new method is applied to obtain the approximate solutions of the fractional coupled MKdV equation.The fractional Lagrange multiplier is accurately determined by the Laplace transform and the nonlinear term can be easily handled by He’s polynomials.The results demonstrate accuracy and fast convergence of this new algorithm.

variational iteration method;Laplace transform;homotopy perturbation method;fractional equation;nonlinear equation

将变分迭代法、同伦扰动法和Laplace变换相结合应用于分数阶非线性发展方程近似解的求解，其中Laplace变换可准确方便地求得分数阶的Lagrange乘子，而He的多项式可简单地处理方程中出现的非线性项，将新的处理方法应用到分数阶耦合的MKdV方程，结果表明该方法具有较高的精度和收敛性。

变分迭代法；Laplace变换；同伦扰动法；分数阶方程；非线性方程

A

O175.29

10.3778/j.issn.1002-8331.1404-0192

DONG Lihua,LIU Yanqin.New approximate solutions of fractional nonlinear equations.Computer Engineering and Applications,2014,50（23）：1-3.

山东省优秀中青年科学家科研奖励基金（No.BS2013HZ026）；山东省自然科学基金（No.ZR2013AQ005）。

董立华（1965—），女，教授，研究方向为函数论；刘艳芹（1981—），女，博士，副教授。E-mail：yanqinliu@dzu.edu.cn

2014-04-14

2014-05-27

1002-8331（2014）23-0001-03

CNKI网络优先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1404-0192.html