基于Matlab/simulink的SVPWM仿真实现

耿翠红 曹以龙

(上海电力学院电气工程学院，上海 200090)

随着计算机控制技术与电力电子技术的发展，空间矢量脉宽调制(SVPWM)技术越来越被广泛地应用于交流变频调速系统中[1]。SVPWM是通过控制三相功率逆变器的6个IGBT的不同开关模式产生PWM波，使逆变器的输出电流近似于理想的三相对称正弦电流。不同于传统的正弦脉宽调制(SPWM)方法，SVPWM着眼于使形成的磁链轨迹跟踪由理想三相正弦电压源供电时形成的基准磁链圆[2]。因此，SVPWM通常也称为磁链跟踪控制技术。此外，与SPWM相比较，SVPWM控制策略可有效降低电机的转矩脉动，提高系统的动静态性能，增加直流电压的利用率，且更易于实现数字化[3]。

笔者主要介绍SVPWM的基本原理及其控制算法，并以永磁同步电机(PMSM)为应用对象，在Matlab/simulink环境下建立了系统的仿真模型，验证该方法的正确性和有效性。

1 SVPWM基本原理①

电流整流后经逆变电路输出PWM波进行控制，图1为三相电压源逆变电路的拓扑结构。将逆变器三相桥臂上的6个IGBT看作理想开关，同一桥臂上的上、下两个开关管互锁[4]。为方便研究，定义开关量Sx(x=a、b、c)，并规定当Sx=1时，上桥臂导通；当Sx=0时，下桥臂导通[5]。

显然，(Sa、Sb、Sc)将产生8种不同的组合，包括6个有效矢量：U1(0 0 1)、U2(0 1 0)、U3(0 1 1)、U4(1 0 0)、U5(1 0 1)、U6(1 1 0)和两个零矢量U0(0 0 0)、U7(1 1 1)[6]。

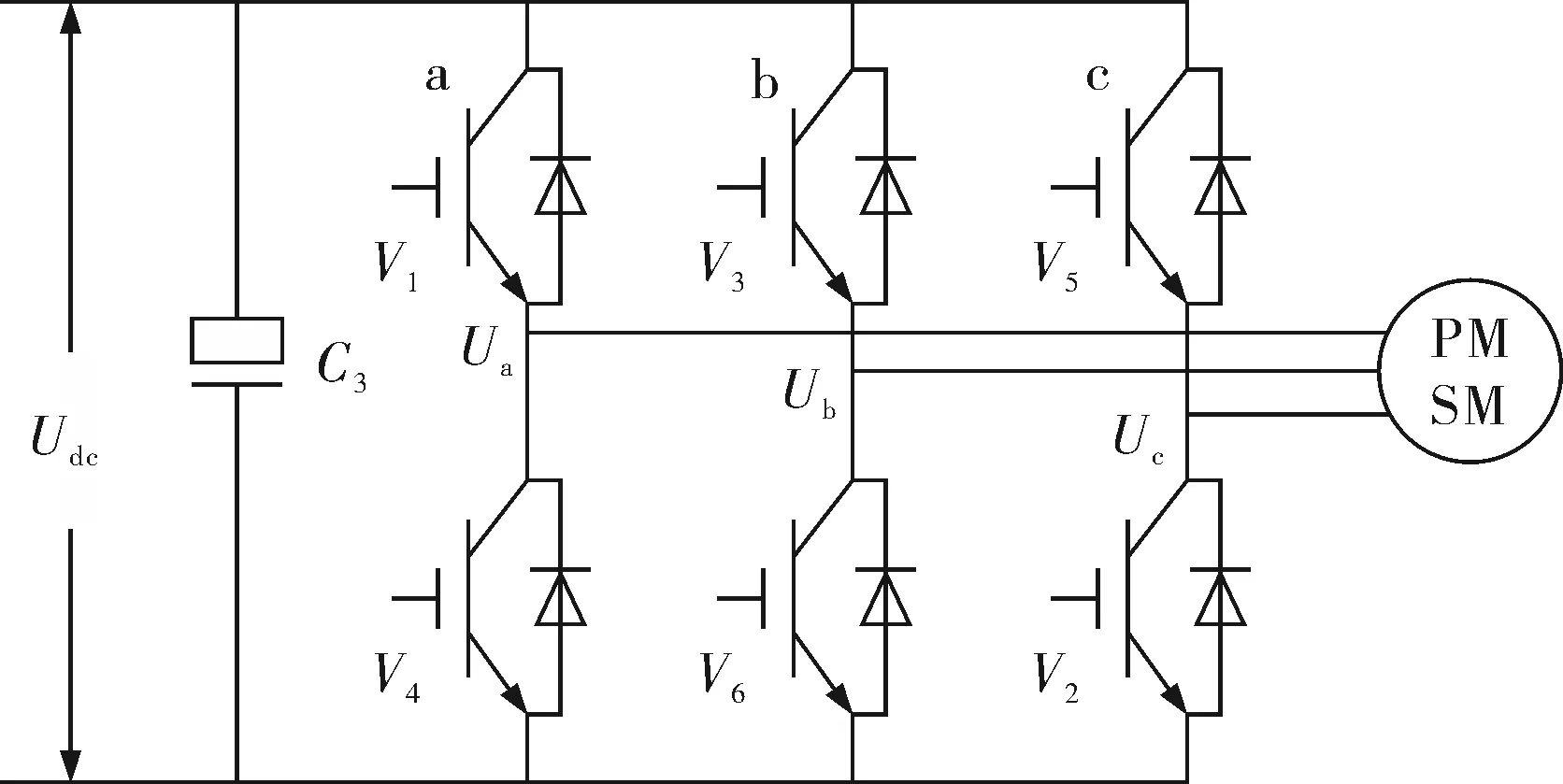
图1 三相电压源逆变器结构示意图

根据空间矢量原理便可得到8个基本电压矢量的大小和位置(图2)。

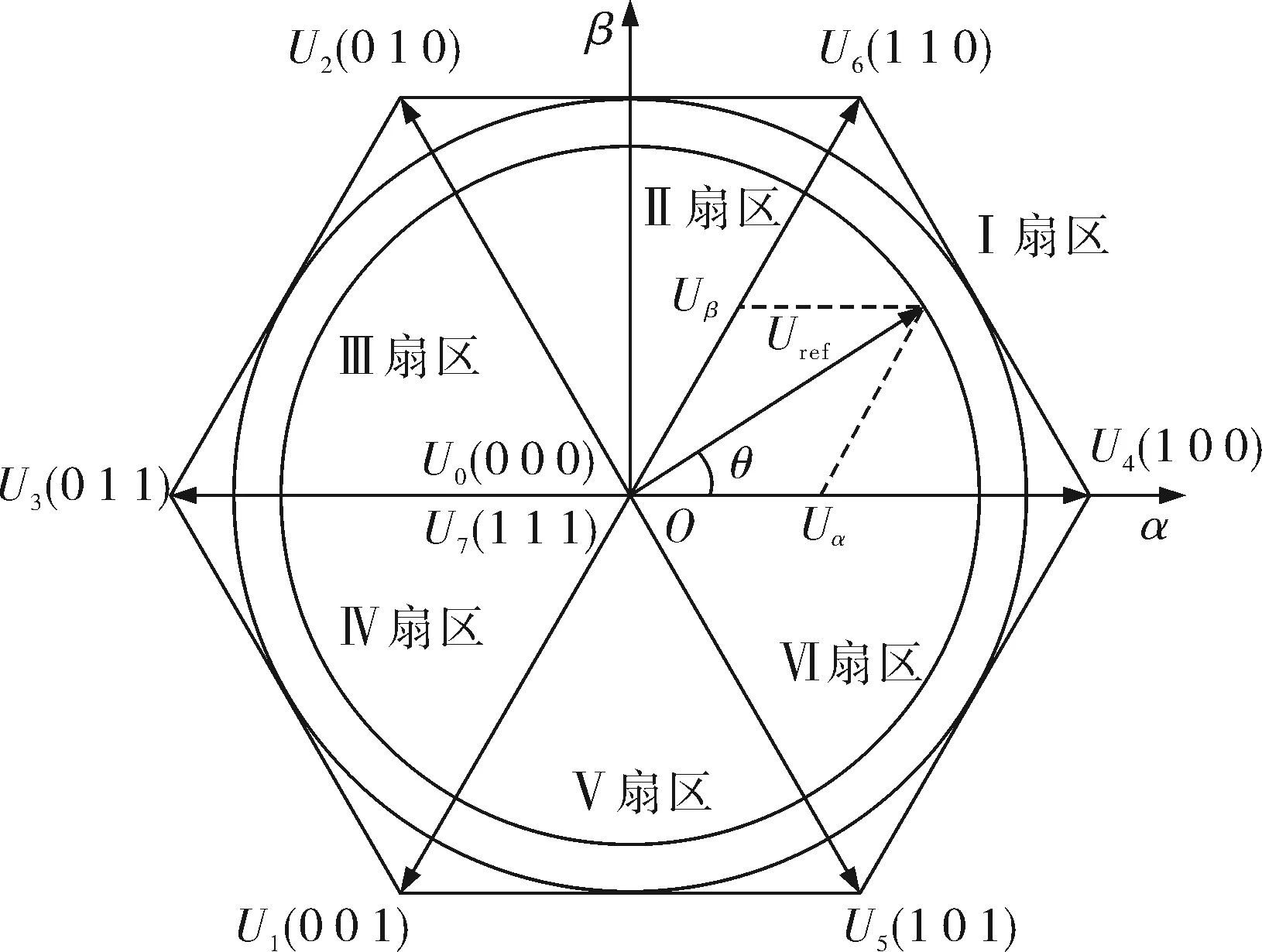
图2 基本矢量分布

经计算可知，6个基本空间矢量的模长相同，都为2Vdc/3。空间矢量就是利用上述8个空间矢量等效合成每个扇区中任意的参考电压矢量Uref[7]。为得到所需脉冲的宽度，需要知道相邻两个基本矢量的作用时间T1、T2[8]。

2 SVPWM的实现方法

根据SVPWM原理，可将SVPWM的实现步骤为：Uref所在扇区判断；基本矢量作用时间计算；矢量切换点的计算和PWM波的形成。

2.1 扇区的判断

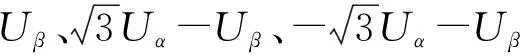
(1)

设定：

则可能的组合共有6种。令N=A+2B+4C，Uref所在扇区便可由N的取值确定，其对应关系见1。

表1 Uref所在扇区与N值的关系

2.2 基本矢量作用时间计算

以Uref在第Ⅰ扇区时为例进行分析，根据图2可得[10]：

(2)

其中Ts为采样周期，T4、T6分别为空间矢量V4、V6的作用时间。求解可得[11]：

(3)

同理可求得在其他扇区时各个矢量的作用时间，为方便求解，可定义：

(4)

则对于不同扇区的T1、T2可按表2取值[12]。

表2 矢量作用时间与所在扇区的关系

2.3 矢量切换点的计算

对于矢量切换点的计算，以第Ⅰ扇区7段式SVPWM为例，由其三相PWM调制模式图(图3)可以得到其矢量切换点：T01=T-T1-T2/4、T02=T01+T1/2、T03=T02+T2/2。其他扇区同理可得，整理结果见表3。其中，Tcm1、Tcm2、Tcm3为晶闸管的切换时间[13]。

图3 第一扇区三相PWM调制模式

扇区ⅠⅡⅢⅣⅤⅥTcm1T02T01T01T03T03T02Tcm2T01T03T02T02T01T03Tcm3T03T02T03T01T02T01

3 SVPWM方法的仿真实现

根据SVPWM产生原理和控制算法流程，可在Matlab/simulink中搭建其仿真模型。判断空间矢量所在扇区仿真如图4所示。

图4 空间矢量所在扇区判断模型

由X、Y、Z的值和采样周期计算基本矢量作用时间T1、T2的仿真实现如图5所示[14]。

图5 计算基本矢量作用时间T1、T2模型

基本矢量切换点的切换时间Tcm1、Tcm2、Tcm3仿真实现如图6所示[15]。

图6 计算切换时间Tcm1、Tcm2、Tcm3的模型

4 仿真结果及其分析

为了验证所建模型的正确性，结合PMSM进行仿真，并设电机功率P=2kW，直流电压Udc=310V，定子绕组电阻Rs=2.875Ω，d相绕组Ld=8.5mH，q相绕组Lq=8.5mH，转子磁场磁通φf=0.175W，转动惯量J=0.8g·m，极对数p=4。仿真系统如图7所示，得到转子转矩、转子转速仿真结果如图8所示。从仿真波形可知，该系统具有较快的响应速度，启动后转矩保持恒定，转速和转矩的超调量均在允许的范围内。

图7 基于SVPWM的系统仿真模型

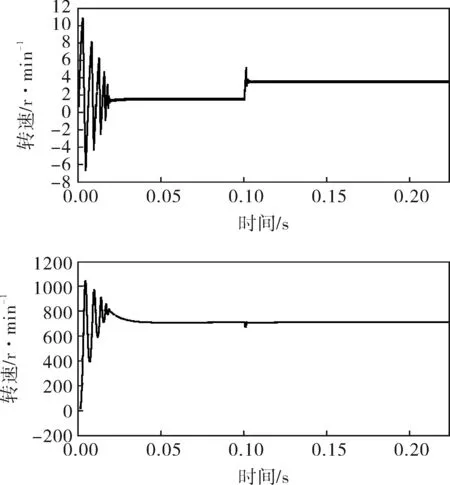
图8 转子转矩和转速波形

5 结束语

根据SVPWM的基本原理，在Matlab/simulink环境下，构建了基于SVPWM的PMSM系统的仿真模型，仿真结果表明，系统具有良好的动静态性能，从而验证了SVPWM方法的有效性。