多边形图形矢栅混合模型的改进及编码方法*

邱 国 清

(闽南师范大学 计算机学院， 福建 漳州 363000)

矢栅混合模型和矢栅一体化模型是数据模型研究的两个部分。其中，矢栅混合模型是将矢量结构和栅格结构的数据不加任何处理分别存储在同一个空间数据库中，当需要使用时只需将两种数据分别调入，这样就可以极大地提高地图编辑对象的信息量和准确性，矢栅混合模型已经在GIS和制图中得到了广泛的应用，但该模型数据重复存储占用了大量的存储空间[1]，为了弥补该缺点，提出了将存储空间中的矢量数据和栅格数据进行编码处理，同时对这两种编码进行压缩，以达到减少存储空间和提高效率的目的。

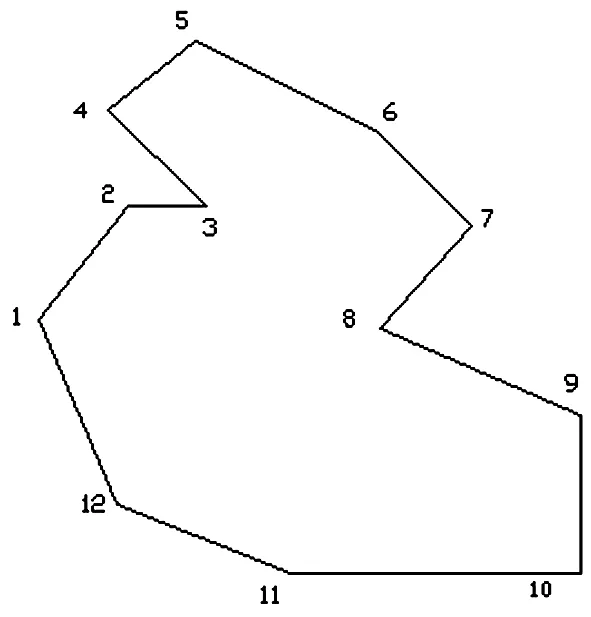
图1:复杂多边形图形

1 矢量数据编码及压缩方式

矢量数据结构是通过记录坐标的方式，尽可能精确地表示点线多边形等地理实体[2]，该数据结构精度高，易于空间信息的可视化表达[3]。矢量数据的编码及压缩比较简单而且方法有多种。

2 栅格数据的编码

栅格数据结构又称为网格数据结构，每个小方格用(x,y)坐标表示，其最明显的特点就是属性明确，定位隐含[4]。

2.1 四叉树原理

四叉树编码方式是栅格数据编码最常用的方法之一，该编码方式将图形分为四个部分，逐块检查其格网属性值，但该编码方式最大缺点在于转换的不定性，同一个图形可能会有多种不同的四叉树，这样就不利于形状分析和模式识别，为此还需要将四叉树转换成二叉树，这样就能保证只得出一棵对应的编码树。

2.2 四叉树转换成二叉树

利用霍夫曼原理[5]将四叉树转换成二叉树，该基本原理是按照字符出现概率的大小，概率大的字符分配短码，概率小的字符分配长码来构造最短的平均码长，以图1为例，假设点1、2、3的属性值为1，点4、5、6、7的属性值2，点8、9、10、11的属性值为3，点12的属性值为4，该图形编码中每个像素元的属性值出现的概率大小计算如表1所示。

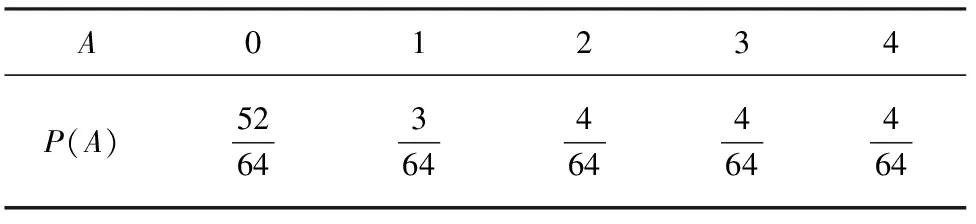
表1:概率表

用霍夫曼编码方法，对属性值进行编码，其编码过程如表2所示。

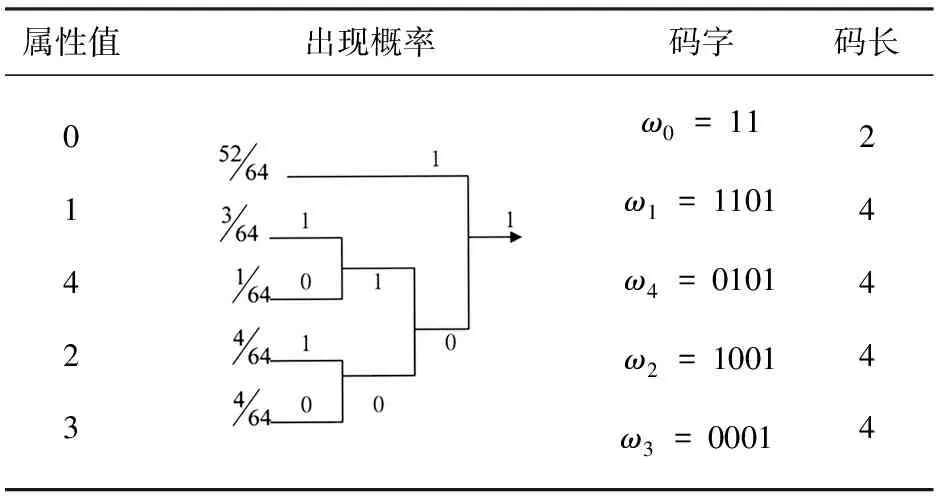
表2:编码过程

2.3 霍夫曼编码树

表2的编码过程可用图2的编码树来表示。

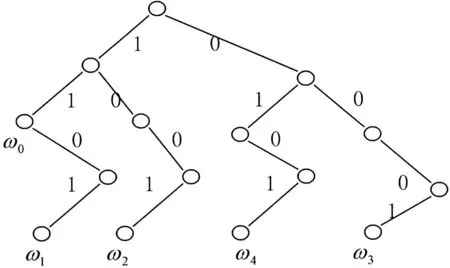
图2:霍夫曼编码树

3 Morton码的原理

Morton码的计算如下[6]：

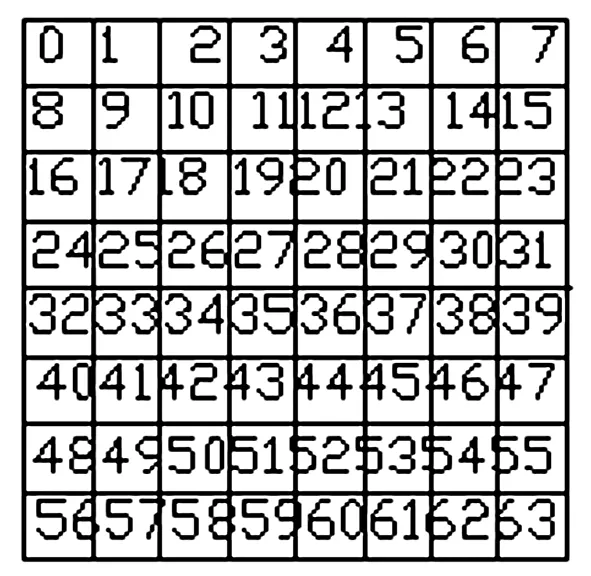
图3:Morton码

图4:Morton码的计算过程

这样就可以行列表示二维栅格阵列图形，用Morton码写成二维数组，通过Morton码来确定节点的坐标。

图5:复杂多边形转化后的编码

4 矢栅数据转化后的存储编码

对于矢量数据结构才采用元子空间填充来表达。图1是复杂多边形的原始矢量数据结构，采用元子空间填充后，转化成图5复杂多边形的十进制四叉树。

栅格数据结构本身就可以直接采用十进制四叉数编码方式存储，假设图1中点1、2、3、4、5、6、7的属性值为，点8、9、10、11、12的属性值为2，其它都为0，那么多边形图形的栅格结构为图6所示，

图6:多边形图形栅格数据结构

通过图5和图6可以看出，将矢量数据结构采用元子填充后，矢量数据和栅格数据都可以采用十进制四叉树编码，从而保证了编码的一致性。

5 总结

矢栅混合模型中的矢量数据和栅格数据转换同样的编码，对于重复的数据不需要在同一个数据库中反复存储，节省了存储空间，混合模型中数据结构转换成同一个格式，这样在数据处理更加方便，提高了编码的效率。

〔参考文献〕

[1]闫浩文，等. 计算机地图制图原理与算法基础[M].北京：科学出版社,2007：108-109.

[2]何嘉珈. 矢栅数据一体化存储技术研究[J].科技资讯，2009，(26)：233.

[3]王昌、滕艳辉. 矢量栅格一体化数据结构设计与应用[J]. 计算机工程，2010，20(36)：88-89.

[4]王建、杜道生. 矢量数据向栅格数据转换的一种改进算法[J].地理与地理信息科学，2004，20(1)：31-34.

[5]付先平. 多媒体技术及应用[M]. 北京：清华大学出版社，2007：53-55.

[6]艾自兴，龙毅. 计算机地图制图[M].武汉：武汉大学出版社,2005:37-45.