基于TC控制与干扰观测器的Smith预估控制
李 光 郑恩让
(陕西科技大学电气与信息工程学院,西安 710021)
工业过程中滞后现象的存在对系统的稳定性和动态品质影响非常大,会使系统的超调量增大,响应时间变长,更有甚者会使系统出现振荡、发散的情况,导致系统的控制效果降低。瑞典科学家Smith于1957年提出的Smith预估器从理论上解决了时滞对系统的影响,但是需要知道对象的精确数学模型,而且只能用于定常系统,所以在实际应用中受到限制。另外该方法还存在鲁棒性差和抗扰性差的问题,因此许多文献都提出了扩展型或改进型的方法:文献[1~6]把自抗扰技术与Smith预估器相结合;文献[7]通过重复控制的方法对控制器参数进行了自整定;文献[8,9]对Smith预估器做了修改,增强了抗扰性。
笔者对传统的Smith预估器也进行了两方面的改进:首先采用一种控制结构简单、不需要精确模型、动态响应速度可调且易于实现的鲁棒控制器(TC控制器);其次,加入了干扰观测器,增强了系统的抗扰性。通过对典型时滞系统的大量仿真,结果表明:当数学模型参数τm变化50%时,系统输出仍然平滑而且响应速度快,验证了该方法对于稳定时滞系统的有效性和可行性。
1 改进型Smith预估控制①
为了提高传统Smith预估控制器的鲁棒性和抗扰性,使用TC控制器代替PID控制器,并且加入了干扰观测器,系统的结构如图1所示,当被控对象与数学模型完全匹配时系统的闭环传递函数为:
(1)

图1 改进型Smith预估控制器框图
1.1 TC控制器
1992年,意大利学者Tornambè A和Valigi P提出了TC控制器[10],其核心在于构造观测器获得对扰动的估计和补偿以提高控制效果,该方法控制结构简单,不需要精确模型,易于在工业过程中实现。系统的相对阶数为一时,TC控制律为[11]:
(2)

h0——可调预期动力学参数,决定系统的响应速度;
k0——可调参数,决定系统的鲁棒性;
y——系统输出;
yr——系统给定;
ξ——中间变量。
1.2 稳定时滞系统控制器设计
考虑如下形式的一阶稳定时滞系统:
(3)
由式(2)得到TC控制器的表达式:
(4)
a=h0+k0,b=h0k0
(5)
E(s)=Yr(s)-Y(s)
(6)
把式(3)、(4)代入式(1),得到闭环传递函数:
(7)
笔者按照文献[12]的ITAE控制系统优化设计方法来进行参数整定。将特征多项式Ts3+s2+aKs+bK的系数与基于ITAE指标的Φ(s)的最优系数进行对比,求解得到参数a、b的表达式:
(8)
(9)
其中ωn是系统自然频率。
按照上述方法也可以得到二阶稳定时滞系统的参数表达式:
(10)
(11)
(12)
2 干扰观测器
干扰观测器的基本设计思想是将外部力矩干扰和模型参数变化造成的实际对象与名义模型输出的差异统统等效为控制输入端,即观测出等效干扰,在控制中引入等量的补偿,实现对干扰完全抑制。干扰观测器的原理如图2所示。

图2 干扰观测器原理框图
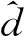
(13)
由图1可得到扰动输入的传递函数:
Yd(s)=Gp(s)[1-Q(s)e-τs]e-τsD(s)
(14)

Q(s)的设计是干扰观测器设计中一个非常重要的环节。首先,为使Q(s)Gp-1正则,Q(s)的相对阶应不小于Gp-1的相对阶;其次,Q(s)宽带的设计是在干扰观测器的鲁棒稳定性和干扰抑制能力之间的折中[13]。
设Gp(s)的名义模型为Gn(s),则不确定对象的集合可以用乘积摄动来描述,即:
Gp(s)=Gn(s)[1+Δ(s)]
(15)
式中Δ(s)——高频振动。
由鲁棒稳定性定理可知,低通滤波器Q(s)鲁棒稳定的充分必要条件:
(16)
当被控对象与数学模型失配时,被控对象与预估器模型的误差为:
(17)
考虑只有τm变化时,对式(17)通过泰勒级数展开:
Df(s)=Gp(s)[0.5(τ-τm)s2-(τ-τm)s]F(s)
考虑一阶时滞对象:
(18)
(19)
这样通过设计滤波器F(s)就可以减小模型失配时的误差。
3 仿真研究
为验证笔者提出的改进型Smith预估控制方法,以下用该方法和文献[14]中的方法对工业过程中典型的一阶和二阶稳定时滞系统进行仿真研究。
3.1 一阶稳定时滞系统仿真
考虑如下一阶稳定时滞系统:
(20)
根据文献[14]中的方法,选取PI控制器的参数为Kp=0.037 5,Ti=3。根据式(5)、(8),选取TC控制器参数为h0=17.3,k0=2.7,滤波器Q(s)=1/(3s+1),F(s)=1/(150s+1)。
在模型匹配时,为验证系统的跟踪性能和抗扰性,分别在t为1、100s时输入单位阶跃信号和0.2的阶跃干扰信号,响应曲线如图3所示。

图3 一阶对象模型匹配时系统的响应曲线
在模型失配时,为验证系统的鲁棒性和抗扰性,使数学模型参数τm变化50%时的响应曲线如图4、5所示。

图4 一阶对象模型τm减小50%时的响应曲线

图5 一阶对象模型τm增大50%时的响应曲线
从图4、5可以看出,虽然预估器模型的纯滞后时间变化幅度大,但该方法仍然可以很好地控制系统,在一定程度上不存在所谓的模型失配问题。
3.2 二阶稳定时滞系统仿真
考虑如下二阶稳定时滞系统:
(21)
按照3.1节所述,选取PID控制器的参数为Kp=0.05,Ti=5,Td=6/5。TC控制器的参数为h0=102,k0=0.5,滤波器Q(s)=1/(3s+1)2,F(s)=1/(150s+1)。
在模型匹配时,在t分别为1、100s时输入单位阶跃信号和0.2的阶跃干扰信号,响应曲线如图6所示。

图6 二阶对象模型匹配时系统的响应曲线
在模型失配时,模型参数τm变化±50%时的响应曲线如图7、8所示。

图7 二阶对象模型τm减小50%时的响应曲线
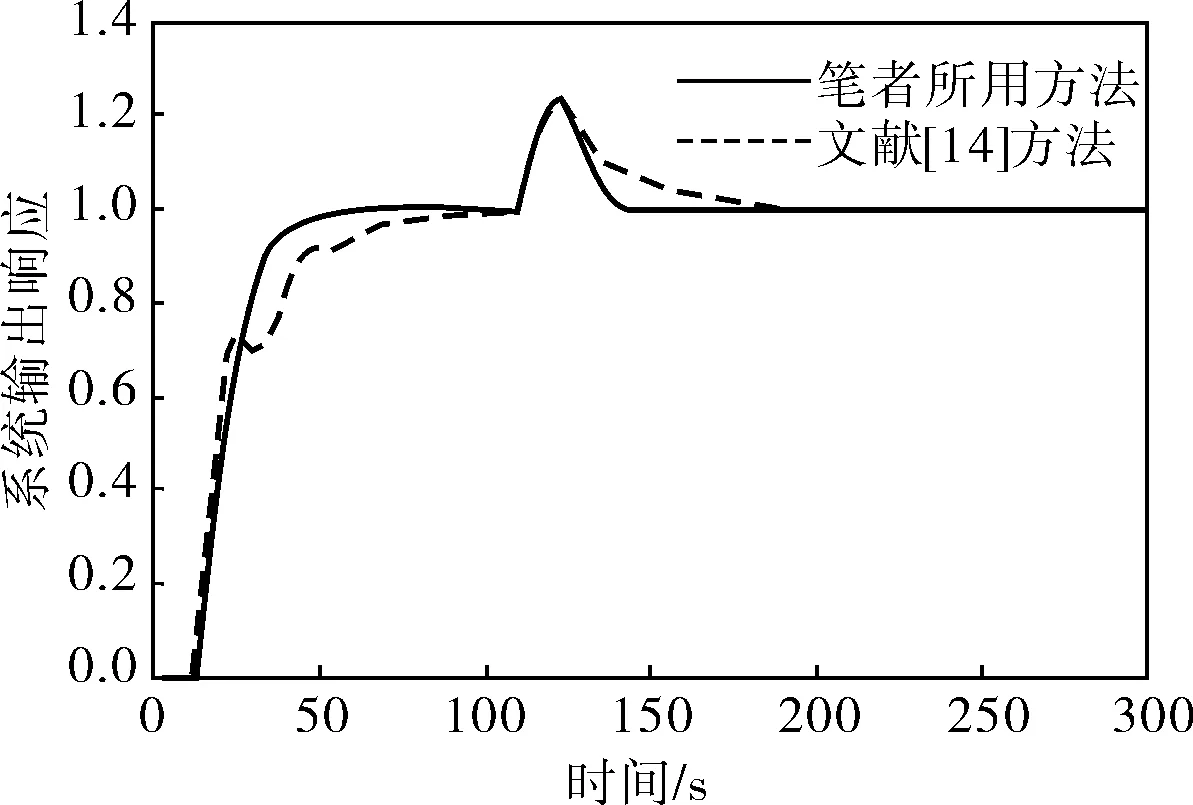
图8 二阶对象模型τm增大50%时的响应曲线
同理,从图7、8可以看出,笔者所述方法仍然可以有效地控制二阶稳定时滞系统。
由仿真结果可知,模型参数变化±50%时,笔者所述方法的系统输出仍然平滑而且响应速度快,克服了传统Smith预估器鲁棒性差和抗扰性差的缺点,提高了控制系统的品质。
4 结束语
传统Smith预估控制在实际中控制效果不佳,模型失配时鲁棒性和抗扰性差。针对这两方面提出了一种不依赖于精确数学模型、结构简单、响应速度快、易于实现的TC控制器与干扰观测器相结合的改进型Smith预估器。通过对典型稳定时滞系统的大量仿真研究,可以发现该方法克服了传统Smith预估器的缺点,明显地改善了控制系统的品质。

