基于第一扇区坐标分量的SVPWM快速算法

荣 飞 董兴发

(1.山西同煤集团煤峪口矿，山西 大同 037000； 2.太原理工大学机械工程学院，太原 030000)

空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)技术是一种比SPWM技术更为先进的、计算机可高度介入的脉冲宽度调制(Pulse Width Modulation，PWM)方法。它具有谐波含量少、开关损耗小和直流电压利用率高的优点，且磁链轨迹更逼近圆形，转矩平稳，因此得到了日益广泛的应用[1]。传统的SVPWM算法涉及到大量的运算，主要是三角函数运算和矩阵运算，这大大增加了控制器的负担和程序占用的存储空间[2]。

笔者提出了一种新型的SVPWM快速算法，该算法能根据参考矢量的坐标分量迅速判断出参考矢量所在的扇区，且仅需根据坐标分量计算出第一扇区的时间，即可求出其他相关矢量的作用时间，易于数字化应用，具有很好的实用性。

1 SVPWM快速算法①

1.1 扇区判断

两电平在三坐标轴坐标系空间中的矢量图如图1所示，图中的扇区号经过了顺序调整，该操作的仿真模块如图2所示。

图1 两电平三坐标轴坐标系中的矢量图

Ux，Uy，Uz——参考矢量在坐标系的分量；

V1～V6——两电平空间矢量图的基本向量；

Vref——参考矢量

图2 扇区调整仿真模块

如图1所示，在两电平电压空间矢量图中建立一个与所有扇区严格坐标系，其中3个坐标轴x，y，z分别位于扇区Ⅰ，Ⅱ，Ⅲ的角平分线上。设参考矢量在坐标系的分量分别为Ux，Uy，Uz[3]，即：

(1)

若Uz>0，则扇区可能为Ⅱ，Ⅲ，Ⅳ；Uy<0，则扇区可能为Ⅳ，Ⅴ，Ⅵ,因此若Uz>0且Uy<0，则参考矢量所在的扇区为Ⅳ，于是得出参考矢量所在扇区的判断关系见表1[4]。

表1 扇区判断关系表

1.2 相关矢量作用时间计算

相关矢量作用时间的计算依据的是矢量的平行四边形定则，因此若合成两个不同参考矢量的平行四边形是全等的，则它们的相关矢量作用时间要么相同要么顺序相反。

如图3所示，若参考矢量Vref在第二扇区与第一扇区内的模长相等，且第二扇区的参考矢量经角度变换转化到第一扇区后，与α轴正向的夹角与第一扇区的参考矢量和与α轴正向夹角相等。则这两个平行四边形是全等的。图3中，T11、T12、T21、T22为与参考矢量相关的基本矢量的作用时间，于是得T11=T22,T12=T21。当参考矢量位于第三扇区时，同理可得其作用时间与第一扇区作用时间的对应关系为T31=T11,T32=T12。这样就可以用第一扇区的时间来代替其他扇区的时间。

图3 扇区Ⅱ，Ⅰ作用时间关系

设Vref位于第一扇区，由传统的SVPWM算法可得矢量的作用时间为[5]：

(2)

与式(1)相比较得：

(3)

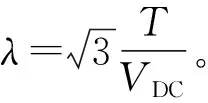
得到的各扇区的矢量作用时间见表2。

表2 各扇区矢量作用时间

于是将参考矢量旋转到第一扇区后，就可以用式(3)来求所有扇区相关矢量的作用时间了，参考矢量转化公式为:

theta=θ-π(N-1)/3

(4)

式中N——扇区数；

θ——参考矢量与α轴正方向的夹角[6]。

2 仿真验证

在Simulink中建立了该算法和传统算法的仿真模型。直流电压设为600V,仿真时间为0.7s，异步电动机参数设置为：额定功率4kW,线电压有效值400V,频率50Hz，二对极RS=1.405Ω，LS=0.005 839H,Rr=1.395Ω，Lr=0.005 839H，Lm=0.172 2H,转动惯量为0.013 1kg·m2，机械负载转矩为30N·m。图4、5分别为逆变器在该算法下输出的相电压波形图和线电压波形图(横轴单位为s，纵轴单位为V)，由输出波形可知该算法是正确的。图6为电机转矩曲线，图7为电机转速曲线，由电机输出的曲线可知，该算法有较好的稳定性。

图4 相电压波形

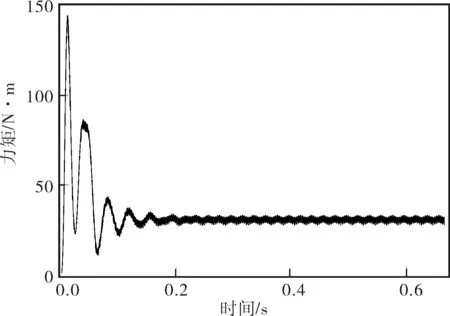
图6 电机转矩曲线

3 结束语

笔者提出了一种基于第一扇区坐标分量的SVPWM算法，简化了扇区判断及相关矢量作用时间的计算量，提高了系统的实时性，系统达到稳态后，运行平稳，且该方法具有很好的实用性。

图7 电机转速曲线