多温区加热炉新型解耦网络及模糊PID控制

鲁照权 黄会娜 孙 木

(合肥工业大学电气工程与自动化学院优化控制技术研究所，合肥 230009)

坯料加热炉有加热一段、加热二段和均热段3个温区。经过3个加热段加热，使坯料达到工艺要求的温度后出炉。3个加热段之间存在着较强的耦合性，同时，每段还具有非线性、时滞性及参数摄动性等特点。因此，坯料加热炉是一个难以控制的MIMO系统。若要对这样的系统实施有效的控制，首先必须解决解耦问题。

解耦方法可以分为传统解耦、自适应解耦及智能解耦等[1,2]。传统解耦方法一般适用于线性定常MIMO系统，对被控过程的数学模型有很强的依赖性，不易实现动态解耦；自适应解耦是一类可行的方法，但其算法比较复杂，而且抗干扰能力和鲁棒性只能在一定范围内满足要求；智能解耦方法对非线性系统的解耦更具有优越性，近年来不少学者对其展开研究[2,3]。

模糊PID控制和BP神经网络均不依赖于系统的数学模型，是处理不确定性、非线性和强耦合性问题的有力工具。模糊PID很容易将人的控制经验融入到模糊控制规则中，其推理方式类似于人的思维模式[4,5]。BP神经网络具有学习和参数调整的优点，能够以任意精度逼近任意解析非线性函数[1,3]。所以将模糊PID控制和BP神经网络相结合是解决MIMO系统非线性、强耦合和带时滞问题的强有力工具。笔者针对多变量、非线性、强耦合和带时滞的三温区加热炉，设计了一种基于新型解耦网络的加热炉模糊PID控制系统[6～8]。仿真结果证明了该系统对实现解耦、克服参数摄动及非线性等问题均具有优良的性能。

1 新型解耦网络及多温区温度控制系统结构①

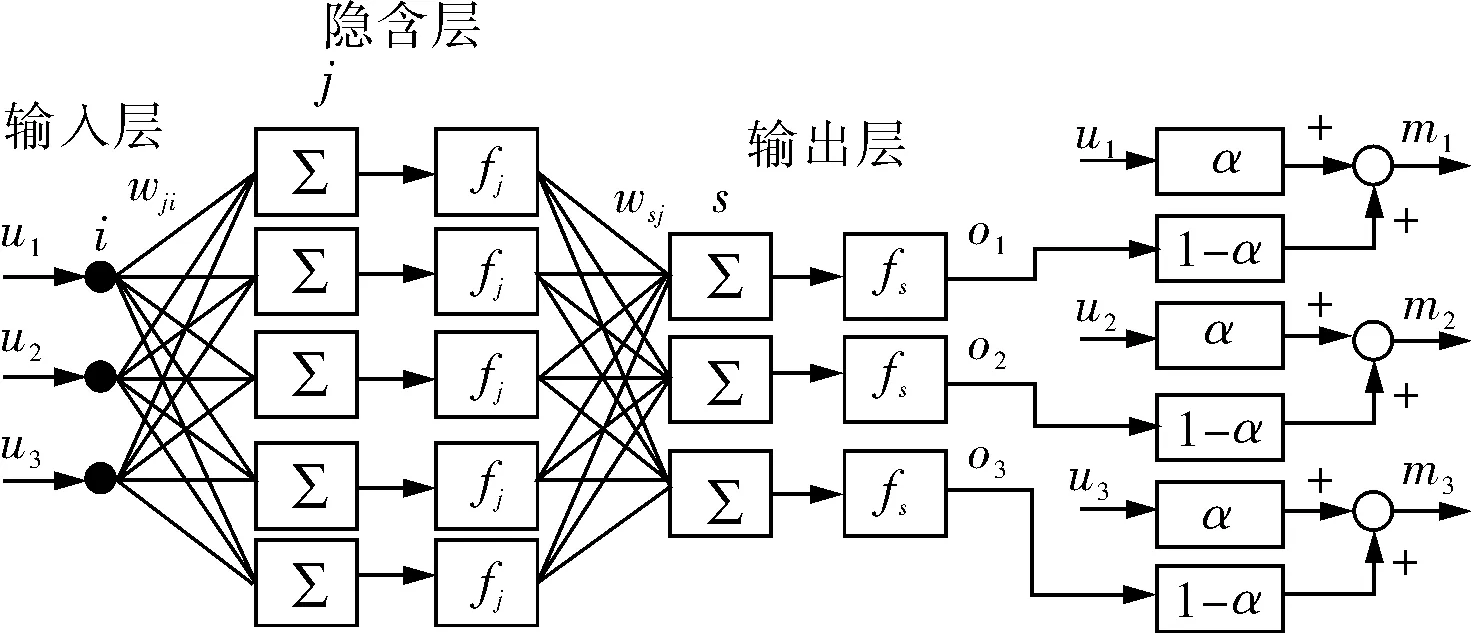
图1 新型解耦网络结构框图

fj——输入层到隐含层的传递函数，为对称饱和线性函数；

fs——隐含层到输出层的传递函数，为线性函数；

i——输入层神经元的个数，i=1,2,3；

j——隐含层神经元的个数，j=1,2,3,4,5；

s——输出层神经元的个数，s=1,2,3

图2 基于新型解耦网络的加热炉多温区

由图1可知ms与us、os的关系表达式为：

ms=α×us+(1-α)×os

(1)

式中s——控制通道数，s=1,2,3；

α——加权系数，取值范围为0～1。

2 BP神经网络学习算法

BP神经网络的学习算法包括前向传播算法和反向传播算法[6]。

2.1 前向传播算法

输入层节点为：

xi(k)=ui(k)

(2)

式中i——输入层神经元的个数，i=1,2,3。

将输入层经过加权系数wji后的输出记为sumj(k)，则隐含层的总输入为：

(3)

将输入层到隐含层的传递函数记为fj(sumj(k))，隐含层的输出值记为bj(k)，则有：

bj(k)=fj(sumj(k))

(4)

其中传递函数fj(sumj(k))为：

(5)

以上各式中j均为解耦神经网络隐含层神经元的个数，j=1,2,3,4,5。

将隐含层经过加权系数wsj后的输出记为sums(k)，则输出层的总输出为：

(6)

将隐含层到输出层的传递函数记为fs(sums(k))，输出层的输出值记为os(k)，则有：

os(k)=fs(sums(k))

(7)

其中传递函数fs(sums(k))为：

fs(sums(k))=sums(k)

(8)

以上各式中，s均为解耦神经网络输出层神经元的个数,s=1,2,3。

2.2 反向传播算法

定义最小均方误差函数为训练的性能指标，则有：

(9)

式中rs(k)——期望输出值；

s——输入输出个数，s=1,2,3；

ys(k)——系统实际输出值。

隐含层到输出层加权系数wsj的修正算法为：

(10)

由于对象参数未知，式(10)中∂ys(k)/∂us(k)不能直接计算。但其仅为一个相乘因子，其大小决定收敛速度，其正负决定收敛方向。因此可用ys(k)和us(k)相对变化量的符号函数近似代替，其符号函数为：

(11)

由式(11)知：

∂us(k)/∂uos(k)=1-α

(12)

联立解式(9)～(12)得：

(13)

(14)

按最速下降法修正隐含层至输出层连接权值,设学习速率因子为η1，则有：

(15)

wsj(k+1)=wsj(k)+Δwsj(k)+α1[wsj(k)-wsj(k-1)]

(16)

由式(15)、(16)知，当∂E(k)/∂wsj(k)=0时，加权系数的梯度调整就卡在了局部极值点,这时可以加入动量项加以改善，式(16)中α1为动量因子,加入动量项后表明加权系数修正不仅与梯度有关，还取决于上一步权值的变化增量。

由式(13)～(16)可得：

wsj(k+1)=wsj(k)+η1δs(k)bj(k)+α1[wsj(k)-

wsj(k-1)]

(17)

由上述ωsj的修正算法可得：

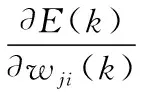
(18)

(19)

(20)

wji(k+1)=wji(k)+η2δj(k)xi(k)+α2[wji(k)-

wji(k-1)]

(21)

式中α2——动量因子；

η2——学习速率因子。

3 模糊PID控制算法

模糊PID调节器由4个部分组成：模糊化、知识库、模糊推理和清晰化[5]。以一通道为例，其结构如图3所示[11]。

图3 一通道模糊PID调节器结构框图

图3中PID调节器采用增量式控制算法，其输入输出关系为：

ui(k)=ui(k-1)+KP[ei(k)-ei(k-1)]+KI[ei(k)]+KD[ei(k)-2ei(k-1)+ei(k-2)]

(22)

模糊PID调节器是基于模糊条件语句描述的语言控制规则。其KP、KI、KD控制规则见表1～3[12]。用NB、NM、NS、ZO、PS、PM、PB描述模糊PID调节器输入、输出变量的状态。

表1 模糊PID KP控制规则

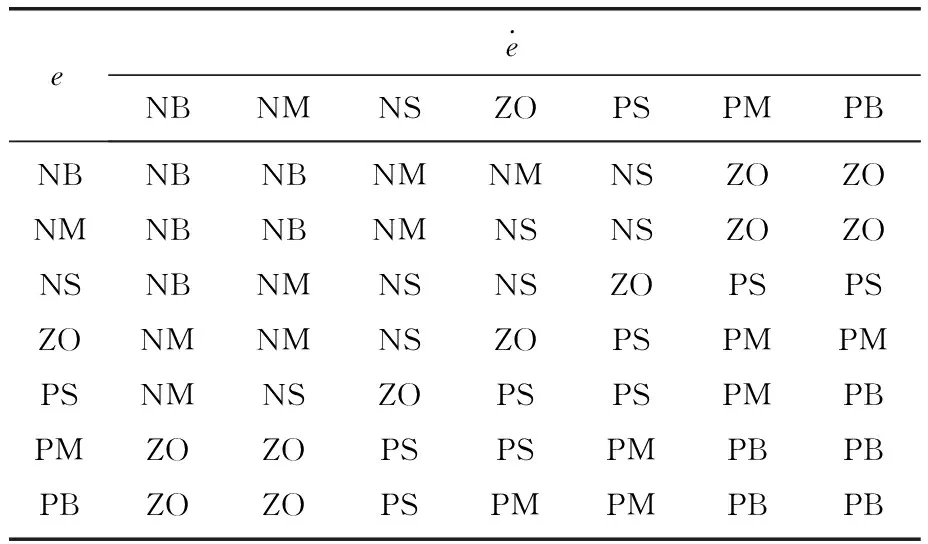
表2 模糊PID KI控制规则

表3 模糊PID KD控制规则

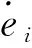
4 基于新型解耦网络的多温区加热炉温度模糊PID控制系统仿真

对图2所示的基于新型解耦网络的多温区加热炉温度控制系统进行训练，学习步长η1=η2=0.075，信号采样点数k=400，加权系数α=0.05，动量因子α1=α2=0.03，输入层到隐含层的加权系数初始值为0.045rands(5,3)，隐含层到输出层的加权系数初始值为0.05rands(3,5)。某多温区加热炉数学描述为：

(23)

式中aij——各个控制量对相应通道输出值的作用系数，i为通道个数，i=1,2,3，j=1,2；

bij——第j通道控制量对第i通道输出值的作用系数，i=1,2,3，j=1,2,3,且i≠j。

为方便起见，定义式(23)中系数矩阵为：

(24)

被控过程的原始系数矩阵为：

鉴于均热段的温度对坯料的出炉温度影响最大，则以下仿真中，温度给定为：

被控过程的系数矩阵分别为原始值、原始值的50%、原始值的250%、原始值的300%，系统的响应曲线分别如图4所示。当系统系数矩阵参数发生大幅度摄动时，基于新型解耦网络和模糊PID控制的三温区加热炉温度控制系统均具有良好的解耦性能和控制品质。

a. 100%

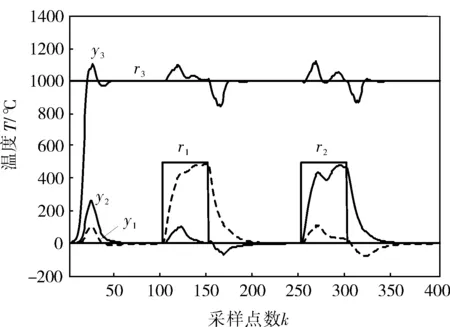
b. 50%

c. 250%

d. 300%

5 结束语

基于新型解耦网络的加热炉温度模糊PID控制系统比较完美地解决了三温区之间的强耦合性、系统参数的不确定性及非线性等问题，各控制通道响应速度快，超调量小，鲁棒性好，抗干扰能力强。因此，该解耦控制方法在多变量耦合系统控制中具有很高的应用价值。