基于小波变换的电缆故障测距研究
姚建红 林 娜 王天明 张玲玉
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.大庆油田电力集团,黑龙江 大庆 163000)
在电缆故障测距中,通过观察实测的故障电缆行波信号,可以看出,有的行波信号上升沿比较缓慢,奇异性较弱,如果用小波变换模极大值法检测奇异点,就会产生一定的误差,而用曲线拟合法则较准确。当测得的行波信号较强时,一般采用小波变换模极大值法确定奇异点,笔者将小波变换模极大值法和曲线拟合法相结合来进行信号奇异点的确定。
1 模极大值法①
信号经过小波变换后,在突变点处相对应的小波系数的绝对值通常都是比较大的,所以信号的局部奇异性与小波变换的模极大值之间存在着一定的关系,即通过小波变换的模极大值在不同程度上的衰减速度可以将信号的局部奇异性检测出来。模极大值法奇异性检测步骤为:
a. 首先对信号进行离散二进制小波变换,选择合适的分解尺度,一般选择的分解尺度为4或5;
b. 将各个分解尺度上小波变换系数对应的模极大值点求出;
c. 利用AD HOC算法,搜索出最大尺度上的每一个模极大值点所对应的模极大值线,将没有在模极大值线上的模极大值点去掉,并逐级地进行搜索,将最后剩下的两个模极大值点保留,则这两个模极大值点对应的时刻就是发射脉冲和第一次反射脉冲起始点所对应的时刻。
2 曲线拟合法
曲线拟合法是指通过曲线拟合获取数据中反射脉冲的上升沿数据的一部分,进而确定出起始点的方法。曲线拟合法进行反射波奇异点检测的具体步骤为[1]:
a. 求取反射波的极值点Fmax,以及极值点所对应的采样序号Tmax,其中对于短路和低阻故障要求极小值,开路故障求极大值;
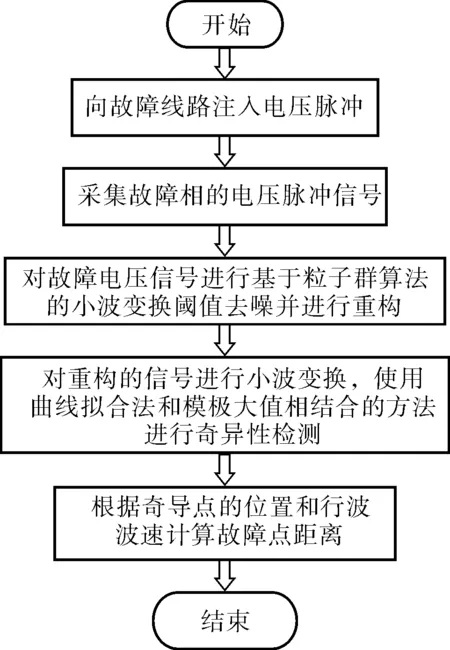
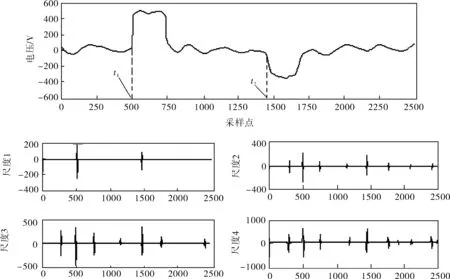
b. 通过所得到的反射波的极值点对阈值区间进行确定,这里以Fmax>0时的情况分析说明,Fmax<0依此类推。当Fmax>0的时候,选取阈值区间为[FL,FR],其中有0 曲线拟合法在进行奇异性的检测时对奇异性较强的信号检测误差较大,会给测距精度带来一定的偏差。而常见的函数空间和函数的局部光滑性质都可以通过小波系数来进行描述。通过对小波系数的描述,不但能够反映信号在整个时域上的频谱含量,而且还可以体现出信号随时间变化而变化的特性。 曲线拟合与模极大值法相结合的奇异点检测方法的基本思想为:首先对去噪后的行波信号用曲线拟合的方法初步确定奇异点Ts,然后求出该拟合曲线上的点Ts处切线的斜率k,若斜率|k|>|kset|,即该点处的反射波上升沿比较陡,则继续通过小波变换模极大值法来重新求取奇异点的位置,否则,就认为该点的信号上升沿较缓慢,该点就是要求的奇异点的位置。 由于曲线拟合法是假设获得的数据之间是存在误差的,通过选择合适的参数,用这个含参数的几何模型对原信号进行逼近,使拟合值尽量地接近检测点的检测值。因此,这里认为所得的拟合函数和原检测信号是逼近的,拟合函数上某一点的斜率反映出原始信号在该点的上升或下降的缓急程度。 设定值kset的选取关系到对测量点的判断,进而影响到故障电缆测距的准确度。如果kset选取过小,则程序会自动认为测量脉冲较陡,直接取模极大值法的结果,导致测量误差;反之,若kset选取过大,则程序会自动认为测量脉冲较缓,直接取曲线拟合法的结果,也会导致测量误差。kset的取值对测量误差的影响见表1。 表1 kset取值对测量误差的影响 经过多次反复试验和与测量结果对比,在本文中kset的取值为2.145。 曲线拟合与小波变换结合的奇异点检测算法的具体步骤为: a. 对获得的故障信号运用曲线拟合法检测奇异点,求出拟合曲线f(t)=at2+bt+c,得到a、b、c的值,求出第一次反射脉冲奇异点位置Ts; b. 将奇异点Ts带入拟合曲线,得到拟合曲线上这点的斜率|k|; c. 将|k|与|kset|作比较,若|k|>|kset|,则说明该点处的信号较强,则继续用小波变换模极大值法来求取脉冲的起始点,反之保留Ts的值; d. 根据步骤c的结果,令t2=Ts,即可求出发射脉冲与反射脉冲的时间间隔Δt=t2-t1,其中t1为发射脉冲时间,Δt将代入电缆故障测距公式L=(vΔt)/2即可求得故障点的距离。 电力电缆故障测距方法实现流程如图1所示。具体的实现步骤为:首先建立电缆故障模型,用直流脉冲信号源向电缆的一端注入低压电流脉冲信号,通过采集器采集到故障相和非故障相的电压行波信号,作为实现电力电缆故障测距的原始数据,将得到.p14文件,通过转换软件转换成.mat文件以便于用Matlab进行行波的故障分析;然后由Matlab进行信号的去噪和奇异点的分析,得到奇异点发生的位置,即奇异点发生的时间;最后将波速和时间代入行波测速公式即可得到电缆故障发生的位置,实现电缆故障的测距。笔者采用文献[2]的去噪方法对采集到的故障信号进行去噪。 图1 电力电缆的故障测距流程 仿真模型的具体参数为: 系统的电源 500V 计算步长 0.01μs 铜导体的截面积 300mm2 铜的电阻率 1.75×10-8Ω·m 交联聚乙烯(XLPE)绝缘相对介电常数 2.3 聚氯乙烯(PVC)护套的相对介电常数 5.5 由于线路上的行波是以多种方式传播的,而每种传播形式中的衰减情况也不同,每种频率的传播形式都对应了各自的波速度,因此行波的速度并不是一个固定值,通常取150~200m/μs。因此,为了更好地消除行波波速的不稳定对电缆故障测距造成精度上的影响,建立一个针对仿真模型中的电缆的测量行波速度的模型(图2)。图2中,两段电缆均为400m,则电缆的总长度为800m。 图2 行波测速模型 图3所示为波形的仿真图,图3a中,曲线拟合法中拟合曲线在求得的t2点的斜率大于设定值,因此采用图3b的模极大值法求得的t2=1 447,由于发射脉冲时间t1=5μs,即Δt=9.47μs,由v=2L/Δt,可得: 可以看出,求出的速度值在电缆参数提供的波速度范围内,说明用该方法所测得的速度值是正确的,同时也说明了笔者所提方法的正确性与可行性。因此,在以下的仿真算法中,均取v=168.95m/μs。 a. 曲线拟合法 b. 模极大值法 3.3.1曲线拟合法对模型的验证 笔者仅对短距离的电力电缆单相低阻接地故障建立了仿真模型(图4),图4中,在400m处发生了单相接地故障。图5所示为采用曲线拟合法对图4所示的单相低阻故障仿真模型采集到的电缆故障电压行波信号进行测距分析。 图4 ATP单相低阻接地故障模型 图5 曲线拟合法波形分析 3.3.2小波变换模极大值法对模型的验证 图6所示为采用小波变换模极大值法求取发射脉冲和第一次反射脉冲起始点。 图6 模极大值法波形分析 3.3.3模极大值和曲线拟合相结合的方法对模型的验证 图7 模极大值和曲线拟合相结合的方法波形分析 运用模极大值和曲线拟合相结合的方法分别对单相开路故障、两相短路故障进行了故障测距,其结果见表2。 表2 电力电缆仿真结果对比 对表2的数据进行分析,不难看出,笔者采用了模极大值法和曲线拟合法相结合的方法进行仿真。通过对反射脉冲的上升沿的判断选取适合的方法进行脉冲起始点的检测,结果证明该方法能够很好地进行脉冲起始点的确定,也证明了kset值的选取是合理的。 笔者结合脉冲波形的特点,采用曲线拟合法和模极大值法相结合来确定脉冲起始点,并通过大量的仿真验证了该方法的可行性。该方法能够很好地检测出反射脉冲起始点位置,提高了电缆故障测距的准确性,通过对拟合函数斜率的判断可以确定出反射脉冲起始点的缓急程度,从而降低了电缆故障测距的误差。3 曲线拟合与模极大值法结合的奇异点检测
3.1 斜率的确定

3.2 算法描述
3.3 算法的仿真验证







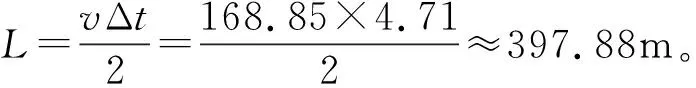

3.4 电力电缆故障仿真结果分析

4 结束语

