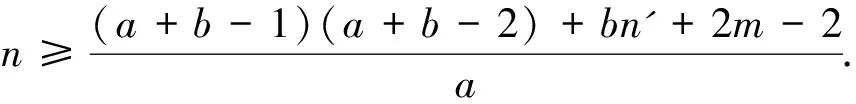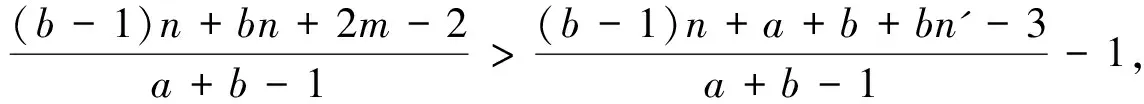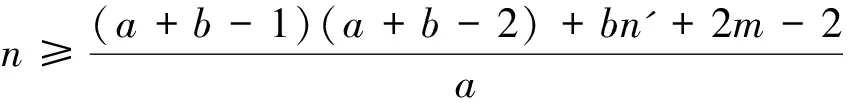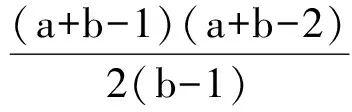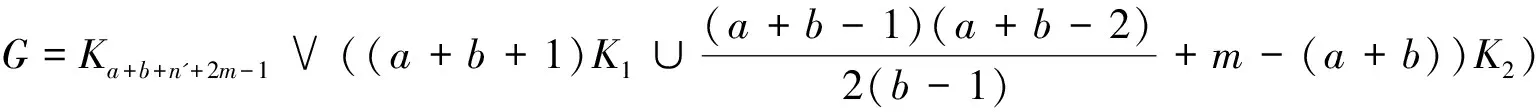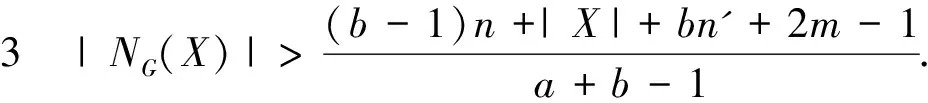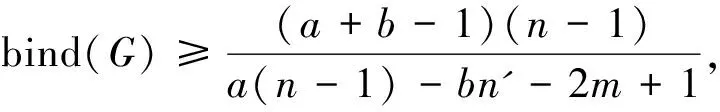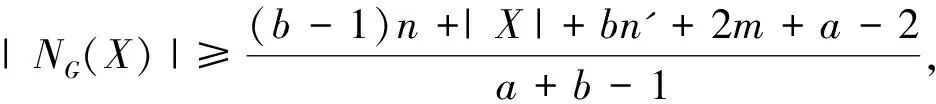特殊框架下分数(f,n',m)-临界消去图的联结数条件*

夏幼明, 张云港, 高炜

(云南师范大学 信息学院,云南 昆明 650500)

1 引 言

在计算机网络中,若将站点看成顶点,站点之间的通道看成顶点之间的边.那么网络中的信息传递问题就可以用图论中的分数因子存在性和因子分解模型来解决.本文忽略站点之间信息传递的方向,所考虑的图均为无向有限简单图.设图G对应某个特定结构的网络,其顶点集和边集分别为V(G)和E(G).对任意顶点x∈V(G),记dG(x)和NG(x)分别为x在G中的度和邻域.δ(G)为G的最小度.对任意S⊆V(G),标记G[S]表示S的导出子图.本文中的其他标记若无特别说明则与文献[1]一致.

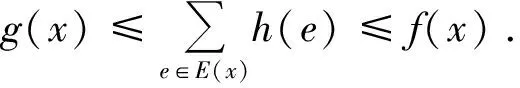
图G的联结数bind(G)用来衡量图G对应网络的易受攻击性和稳定性,其定义为:

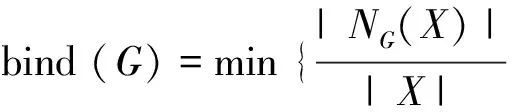
由定义可知,分数(f,n')-临界图和分数(f,m)-消去图分别反映的是网络中部分站点损坏或部分站点之间的连接损坏的情况下,是否还可以进行站点之间的信息传输.而分数(f,n',m)-临界消去图反映的是部分站点和连接同时被损坏的情况下,网络信息传输的可行性.而图的联结数恰恰是反应网络易受攻击性的一个参数,因此从数学上研究它们之间的相互关系对于网络保护和信息流传输都有重要意义.

文献[2]研究了联结数与分数(f,n',m)-临界消去图的相互关系,得到如下结果:

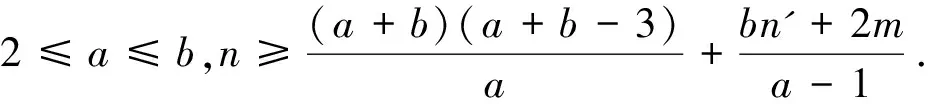
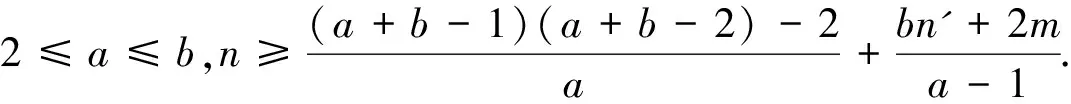
和

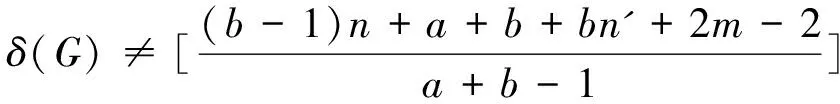
则G是分数(f,n',m)-临界消去图.

这两个结果在一定程度上扩展了文献[3-4]中的相关结论.其他关于分数临界图和分数消去图的结果可参考文献[5-9].在已有结论的基础上,本文继续研究联结数与分数(f,n',m)-临界消去图的关系.指出在a、b同时为偶数的情况下,定理1和定理2中关于联结数的界可以更好,同时对新结论的最优性进行讨论.本文的主要结论如下:

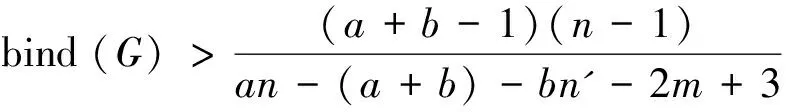
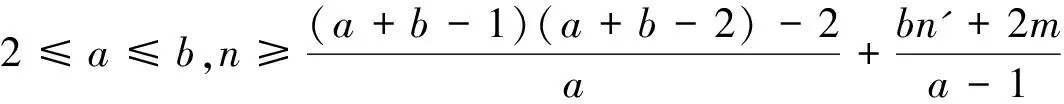
和

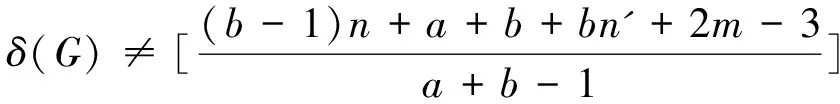
则G是分数(f,n',m)-临界消去图.

定理3和定理4的证明主要运用分数(f,n',m)-临界消去图的充要条件，如下:

引理1[10]设G是一个图,f是定义在V(G)上的非负整值函数.设n'、m是两个非负整数.则G是分数(f,n',m)-临界消去图当且仅当

对所有V(G)的不相交子集S,T成立,其中|S|≥n'.

2 定理3的证明

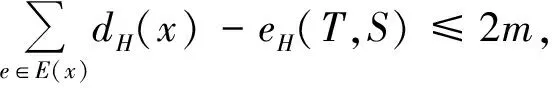
f(S)-f(T)+dG-S(T)≤bn'+2m-1

(1)

其中|S|≥n'.选取S、T使得|T|的值最小.从而对每个x∈T,都有dG-S(x)≤f(x)-1≤b-1成立.这是因为若存在某个x∈T使得dG-S(x)≥f(x),则S和T{x}依然满足(1).这与S和T的选取矛盾.

设d=min{dG-S(x):x∈T}.则0≤d≤b-1且

f(S)+dG-S(T)-f(T)≥a|S|+d|T|-b|T|

从而

bn'+2m-1≥a|S|-(b-d)|T|

(2)

选取x1∈T使得dG-S(x1)=d.我们从以下两种情况分别得到矛盾.

情况1 1≤d≤b-1.

设Y=(V(G)S)NG-S(x1).则x1∈YNG(Y).从而Y≠Ø,NG(Y)≠V(G)且|NG(Y)|≥bind(G)|Y|.可知

n-1≥|NG(Y)|≥bind(G)|Y|=bind(G)(n-d-|S|)

即

(3)

由于a、b都是偶数,可得

(4)

由(4),可知

(5)

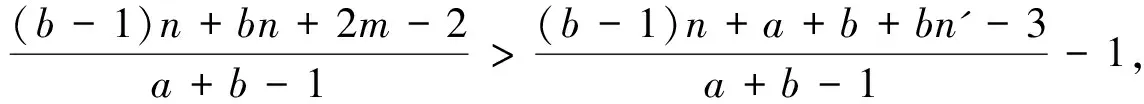
记(5)式的左边和右边分别为A和B,则A-B>0.乘以(a+b-1)(a+b-d)进行整理可得

0<(a+b-1)(a+b-d)(A-B)

=-(d-1)(an-(a+b-1)(a+b-d)-bn'-2m+2)

结合2≤d≤b-1,可知

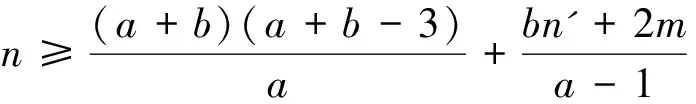
情况2d=0.

在此情况下,首先给出如下断言:

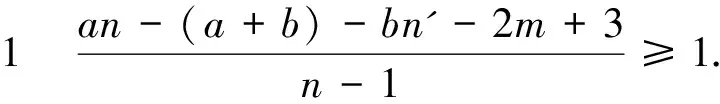
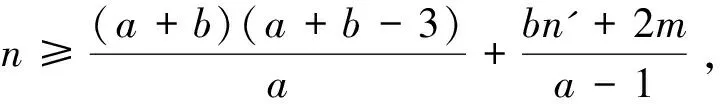
an-(a+b)-bn'-2m+3-(n-1)

=(a-1)n-(a+b)-bn'-2m+4

≥2(a+b-3)-(a+b)+4

=a+b-4≥0.

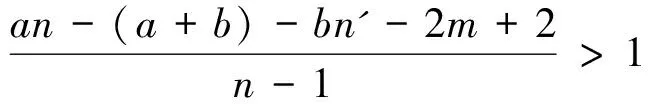
设h=|{x:x∈T,dG-S(x)=0}|且Y=V(G)S.由d=0,可知NG(Y)≠V(G).又根据T≠Ø知Y≠Ø.因此,|NG(Y)|≥bind(G)|Y|.从而有

n-h≥|NG(Y)|≥bind(G)|Y|=bind(G)(n-|S|)

所以

(6)

根据式(2)、式(6)、断言1以及|T|≤n-|S|,得到

bn'+2m-1

≥f(S)+dG-S(T)-f(T)

≥a|S|+|T|-h-b|T|=a|S|-(b-1)|T|-h

≥a|S|-(b-1)(n-|S|)-h=(a+b-1)|S|-(b-1)n-h

=bn'+2m+(a+b)-4≥bn'+2m

矛盾.

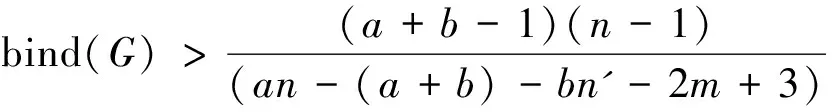
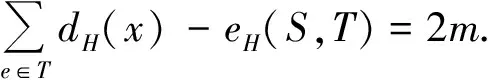
f(S)+dG-S(T)-f(T)

=a|S|-(b-1)|T|

=bn'+2m-2

根据引理1,G不是分数(f,n',m)-临界消去图.从而定理3的联结数条件在a、b都是偶数的情况下是最好的.

3 定理4的证明

为证明定理4,首先给出如下关于分数(f,n',m)-临界消去图邻域条件的引理.

对每个非空独立子集X⊆V(G)成立,且

则G是分数(f,n',m)-临界消去图.

引理2的证明设G满足引理2的条件但不是分数(f,n',m)-临界消去图.显然有T≠Ø.由引理1,存在不相交子集S和T满足

f(S)-f(T)+dG-S(T)≤bn'+2m-1

(7)

其中|S|≥n'.选取S和T使|T|最小.从而有dG-S(x)≤f(x)-1≤b-1对每个x∈T都成立.

设d=min{dG-S(x)|x∈T},则

0≤d≤b-1,δ(G)≤d+|S|

(8)

根据式(8)以及a、b都是偶数,可得

(9)

下面根据d的值分两种情况讨论.

情况1 1≤d≤b-1.

由于a和b都是偶数,可知

(10)

根据式(9)和(10),得

(11)

将(11)式的左边和右边分别记为A和B,则有A-B>0.乘以(a+b-1)(a+b-d)后重新排列可得

0<(a+b-1)(a+b-d)(A-B)

=-(d-1)(an-(a+b-1)(a+b-d)-bn'-2m+2)

结合2≤d≤b-1,得到

(12)

情况2d=0.

设Y={x∈T|dG-S(x)=0}.显然Y≠Ø且Y是独立集.从而有

(13)

情况2.1 |S|+|T|≤n-1.

由式(7)及|S|+|T|≤n,得到

bn'+2m-1

≥f(S)+dG-S(T)-f(T)

≥a|S|+dG-S(T)-b|T|

≥a|S|+|T|-|Y|-b|T|

=a|S|-(b-1)|T|-|Y|

≥a|S|-(b-1)(n-1-|S|)-|Y|

=(a+b-1)|S|-(b-1)n-|Y|+b-1

≥(a+b-1)|S|-(b-1)n-|Y|+1

这说明

与式(13)矛盾.

情况2.2 |S|+|T|=n.

从式(7)和(9)中可知

bn'+2m-1

≥f(S)+dG-S(T)-f(T)

≥a|S|+dG-S(T)-b|T|

≥a|S|+|T|-|Y|-b|T|

=a|S|-(b-1)|T|-|Y|

≥a|S|-(b-1)(n-|S|)-|Y|

=(a+b-1)|S|-(b-1)n-|Y|

=bn'+2m-1

即

dG-S(T)=|T|-|Y|

(14)

且

a|S|+dG-S(T)-b|T|=bn'+2m-1

(15)

从而dG-S(T)是偶数.这是因为Y⊆T.若|T|=|Y|,则由(14)可得dG-S(T)=0.若|T|>|Y|,则根据式(14)以及Y的定义可知dG-S(v)=1对每个v∈T-Y成立.由于|S|+|T|=n,得dG[T-Y](v)=1对每个v∈T-Y成立,且G[T-Y]是一个完美匹配.从而,|T|-|Y|是偶数,同样dG-S(T)也是偶数.

因为a和b都是偶数,得a|S|+dG-S(T)-b|T|是偶数,这与式(15)矛盾.

f(S)+dG-S(T)-f(T)

=bn'+2m-2

从而G不是分数(f,n',m)-临界消去图.就这个意义上来说,引理2中的|NG(X)|条件是最好的.

下面给出定理4的证明.

定理4的证明设G满足定理4的条件但不是分数(f,n',m)-临界消去图.显然T≠Ø.由引理1,存在不相交的子集S和T满足

f(S)-f(T)+dG-S(T)≤bn'+2m-1

(16)

其中|S|≥n'.选取S和T使得|T|最小.则dG-S(x)≤f(x)-1≤b-1对所有x∈T成立.

对所有X⊆V(G),有X≠Ø且NG(X)≠V(G).设Y=V(G)NG(X).显然Ø≠Y⊆V(G).

断言2X∩NG(Y)=Ø.

断言2的证明假设X∩NG(Y)≠Ø,x∈X∩NG(Y).由x∈NG(Y),得到y∈Y和xy∈E(G).

从而,y∈NG(x)⊆NG(X),这和y∈Y=V(G)NG(X)矛盾.

断言3的证明运用以上结果可得

|X|+|NG(Y)|≤n

(17)

和

NG(Y)≠V(G).

(18)

根据式(17)、(18)以及bind(G)的定义,可知

(19)

根据式(19),得到

(20)

从而

(21)

|NG(X)|

由此,断言3成立.

(22)

即,

这和定理4的条件矛盾.

通过断言3、断言4和引理2,可知定理4成立.

参 考 文 献:

[1] BONDY J A,MUTRY U S R.Graph theory[M].Berlin:Spring,2008.

[2] 高炜,高云.关于联结数与分数(f,n',m)-临界消去图的几个注记[J].云南师范大学学报:自然科学版,2012,32(2):53-57.

[3] ZHOU S,SHEN Q.On fractional(f,n)-critical graphs[J].Information Processing Letters,2009,109(14):811-815.

[4] ZHOU S,BIAN Q,LIU H.A remark about fractional(f,n)-critical graphs[J].An.St.Univ.Qvidius Constanta,2011,19(1):365-372.

[5] GAO W,WANG W.Binding number and fractional(g,f,n',m)-critical deleted graph[J].Ars.Combin.,2014,CXIIIA:49-64.

[6] GAO W,WANG W.Anote on fractional(g,f,m)-deleted graphs[J].Ars.Combin.,2014,CXIIIA:129-137.

[7] GAO W,WANG W.A neighborhood union condition for fractional(k,m)-deleted graphs[J].Ars.Combin.,2014,CXIIIA:225-233.

[8] GAO W,WANG W.Degree conditions for fractional(k,m)-deleted graphs[J].Ars.Combin.,2014,CXIIIA:273-285.

[9] GAO W,LIANG L,XU T,et al.Tight toughness condition for fractional(g,f,n)-critical graphs[J].Journal of the Korean Mathematical Society,2014,51(1):55-65.

[10]高炜.关于分数消去图的若干结果[D]．苏州:苏州大学,2012.