一类反应扩散方程的行波解
郑伟强,周小燕,胡萍,彭建奎
(兰州文理学院 师范学院,甘肃 兰州 730030)
非线性现象广泛存在于物理、生物、化学、经济等学科领域,研究某些非线性现象时通常将其转化为非线性偏微分方程来进行描述,从而通过对偏微分方程的计算或数值模拟来了解和解释这些现象.目前已经有很多求解偏微分方程的方法,如齐次平衡法[1]、双曲正切函数展开法[2]、试探函数法[3]、Sine-Gonsine法[4]、辅叠加法[5]、辅助常微分方程法[6]和双函数法[7]等.由于偏微分方程的复杂性,目前对于求解偏微分方程的精确解依然没有统一的方法,因此,寻求新而有效的求解偏微分方程的方法依然是求解非线性方程的重要研究课题之一.本文依照试探函数法解出了一类反应扩散方程的行波解的通解,分析了不同参数情况下解的形式,且对参数m=1时的结果进行了验证.
1 反应扩散方程及行波变换
研究反应扩散方程

(1)

u=u(ξ),ξ=x-ct,
(2)
其中c为波速.将行波解(2)带入方程(1)有

(3)

(4)
2 系统的平衡点
非线性方程解的形式或性质与其定态解的稳定性密切相关,所以研究其定态解的稳定性是非常必要的,而描述系统运动方程的解是否稳定,主要取决于系统在扰动下偏离此解所表征的状态能否回到此状态.为此,李雅普诺夫提出了判断动力系统稳定性的两种方法:李雅普诺夫直接法和李雅普诺夫间接法.本文依照后者对系统的平衡点进行分析.
1)当m=1时,方程(1)可视为Fisher方程的推广,因此方程(4)可写为
(5)
显然,方程(5)有3个平衡位置:(u*,P*)=(0,0),(u*,P*)=(1,0),(u*,P*)=(α,0),相应的特征方程和特征根为:
其中平衡位置(u*,P*)=(0,0)和(u*,P*)=(1,0)都是鞍点,而(u*,P*)=(α,0)在c2>4kνα(1-α)时为结点,在c2<4kνα(1-α)时为焦点.
2)当m=2时,方程(4)可写为
(6)


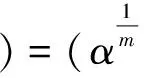

3 连接不同平衡点的异宿轨道
1)当m=1时,根据文献[8]可知:
① 连接鞍点(u*,P*)=(0,0)和鞍点(u*,P*)=(1,0)的异宿轨道为

(7)
② 连接鞍点(u*,P*)=(0,0)和鞍点(u*,P*)=(α,0)的异宿轨道为

(8)
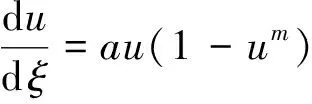

(9)
令z=u-m,则(9)式可写为
(10)
将(9)式两端乘以-m,得
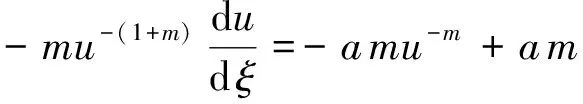
(11)

(12)

(13)
当m=1时,(13)式为连接鞍点(0,0)和(1,0)的异宿轨道,其结果和文献[8]中的结果一致.
(14)
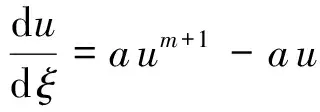

(15)
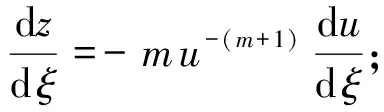
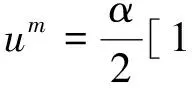
(16)
当m=1时,(16)式和(8)式完全一致,即为连接鞍点(0,0)和结点(α,0)的异宿轨道.
4 结论
本文利用试探函数法求出了当m≥2时,方程(1)的平衡位置,得出了鞍点和鞍点、鞍点和结点之间的异宿轨道,并且验证了当m=1时其结果和文献中的结果相一致;由此得出了一类囊括了许多著名的物理方程(如Fisher方程、Fitzhugh-Napumo方程、Huxley方程[9]等)的行波解的通解.
参考文献:
[1]Wang M L. Solitary wave solution for Boussinesq equation[J]. Physics Letters A,1995,199:162-172.
[2]Parkes E J,Duffy B R. Travelling solitary wave solution to a compound Kdv-Burgers equation[J]. Physics Letters A,1997,229:217-220.
[3]Fan E C,Zhang H Q. A note on homogeneous balance method[J]. Phys Lett A,1998,246:403-406.
[4]Yan C T. A simple transformation for nonlinear waves[J]. Physics Letters A,1996,224:77-84.
[5]Xie Y X,Tang J S. New solitary wave solutions to the Kdv-Burgers equation[J]. International Journal of Theoretical Physics,2005,44(3):293-301.
[6]Xie Y X,Tang J S. A unified approach in seeking the solitary wave solutions to sine-Gordon type equations[J]. Chinese Physics,2005,14(7):1303-1306.
[7]关伟,张鸿庆.求解非线性方程的双函数法[J].高校应用数学学报:A辑,2001,16(2):163-168.
[8]刘式适,刘式达.物理学中的非线性方程[M].北京:北京大学出版社,2000:195-200.
[9]王明新.非线性抛物方程[M].北京:科学出版社,1993:139-180.

