一维等温欧拉方程组的Delta激波解
王 丽
(上海电机学院 数理教学部,上海201306)
一维等温欧拉方程组可以写为如下形式:

式中,ρ为流体的密度;u为流体的速度;p为流体的压强;e为流体的内能;t为时间;x为变量。
式(1)中,压强和音速c分别满足p=ρ和c=1,且内能满足如下关系:

式中,S为流体的熵;R为常数[1]。
在流体动力学的研究中,一般假定流体是定常、等熵或无旋的。然而,对流体做等温的假设在工业上应用广泛,如通过安装制冷设备使得管道流等温,以减少压缩的成本[2]。等温欧拉方程组的重要性不仅体现在生产实践中,它在理论上的应用也颇为广泛[3-6]。
在非线性双曲守恒律的研究领域,黎曼问题是非常基本的问题之一。不同学者借助不同的模型(如欧拉方程组、压力-梯度方程、零压气体等)研究了黎曼问题。一般来讲,黎曼问题的解包含中心波、激波和接触间断。本文将构造另一种形式的黎曼解,即式(1)黎曼问题的Delta激波解。关于Delta激波解,可以参见文献[7-13] 中的结果以及其中的参考文献。
1 预备知识
式(1)的矩阵形式为
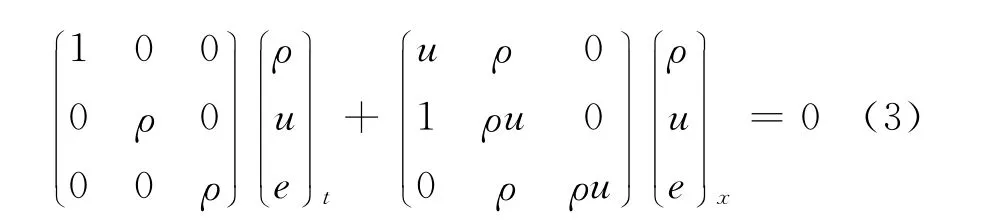
式(3)中的3个特征值为
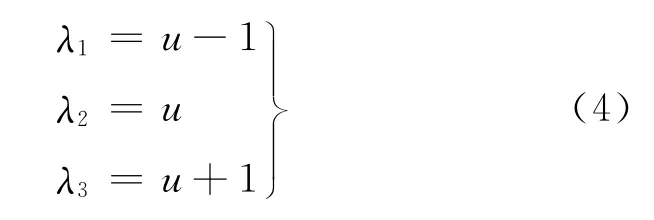
故式(1)是严格双曲的。式(3)相应的右特征向量为

由式(4)、(5)知,

考虑式(1)带有如下初值的黎曼问题:

式中,l、r表示初值的左、右状态。
黎曼问题式(1)、(6)的解包含中心波、激波和接触间断,此处不做赘述。
2 一维等温欧拉方程组的Delta激波解
考虑如下形式的Delta激波解:
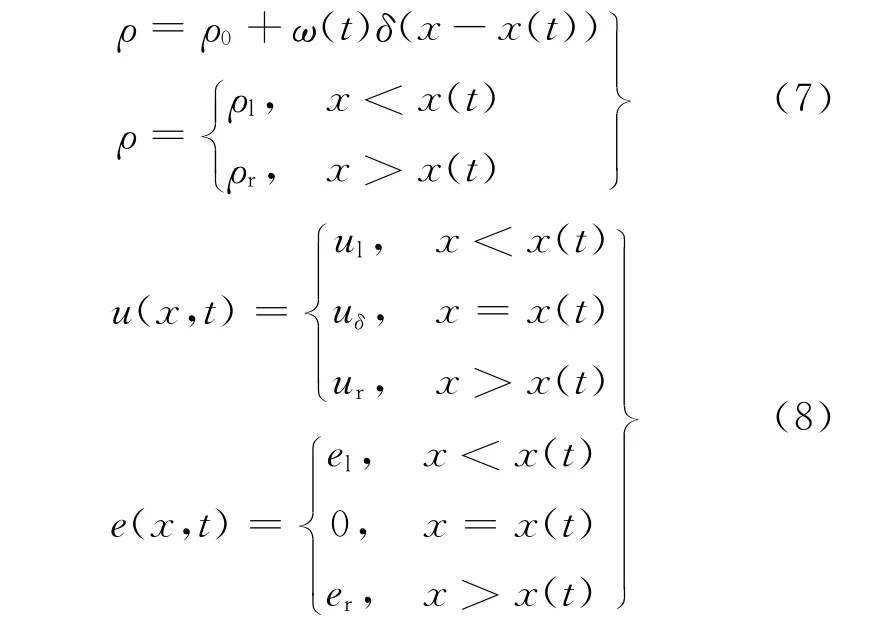
式中,δ(x-x(t))为带有支集x=x(t)的标准狄利克雷测度;ω(t)为Delta激波x=x(t)的权重。若式(7)、(8)是式(1)的一个测度解,则需满足如下形式的Rankine-Hugoniot条件:
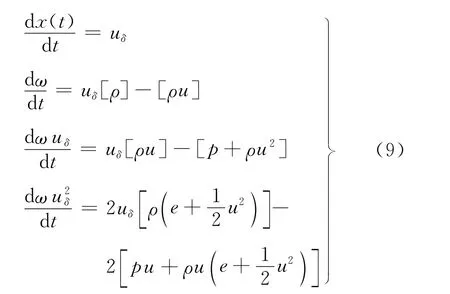
式中,p=ρ。
式(9)的初值条件为
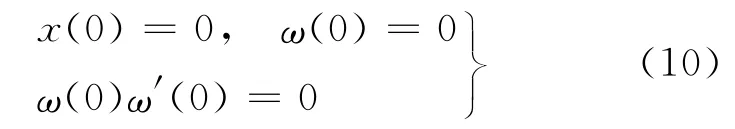
若(ρi,ui,ei)(i=1,r)是常状态,通过求解式(9)、(10),若ρr≠ρl时可得:
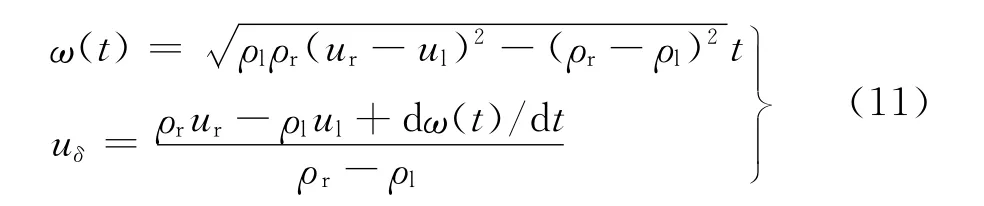
若ρr=ρl,可得:
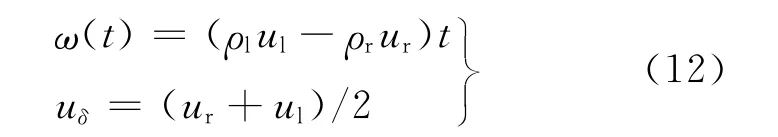
除满足式(11)、(12),Delta激波解还需满足如下的熵条件:
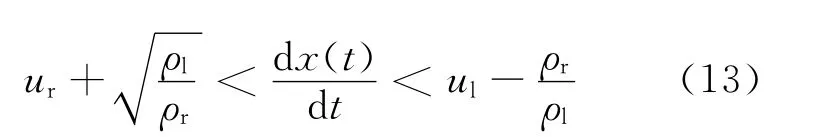
图1所示为Delta激波解示意图。
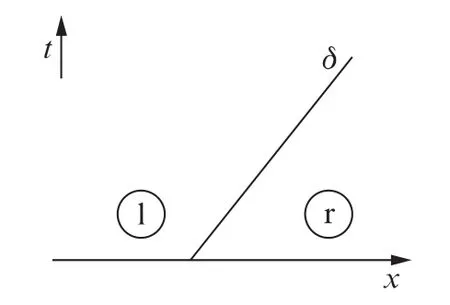
图1 Delta激波解Fig.1 Delta shock wave solution
3 结 语
等温欧拉方程组在工业实际中应用广泛,黎曼问题是流体动力学中非常重要的基本问题。本文重点研究了Delta激波解的结构,这也是目前研究的热门领域。因此,本文在研究对象和研究的问题上都颇具意义。
[1] Chen Guiqiang,Christoforou C,Zhang Yongqian.Continuous dependence of entropy solutions to the Euler equations on the adiabatic exponent and Mach number[J] .Archive for Rational Mechanics and Analysis,2008,189(1):97-130.
[2] Osiadacz A J,Chaczykowski M.Comparison of isothermal and non-isothermal pipeline gas flow models[J] .Chemical Engineering Journal,2001,81(1-3):41-51.
[3] Poupaud F,Rascle M,Vila J P.Global solutions to the isothermal Euler-poisson system with arbitrarily large data[J] .Journal of Differential Equations,1995,123(1):93-121.
[4] Yuen M.Analytical blowup solutions to the 2-dimensional isothermal Euler-poisson equations of gaseous stars[J] .Journal of Mathematical Analysis and Applications,2008,341(1):445-456.
[5] Huang Feimin,Wang Zhen.Convergence of viscosity solutions for isothermal gas dynamics[J] .SIAM Journal on Mathematical Analysis,2002,34(3):595-610.
[6] Bhat H S,Fetecau R C.On a regularization of the compressible Euler equations for an isothermal gas[J] .Journal of Mathematical Analysis and Applications,2009,358(1):168-181.
[7] Korchinski D J.Solutions of a Riemann Problem for a System of Conservation Laws Possessing No Classical Weak Solution[M] .Thsis:Adelphi University,1977:123-150.
[8] Li Jiequan,Zhang Tong,Yang Shuili.The Two-dimensional Riemann Prolem in Gas Dynamics[M] .[S.L.] :CRC Press Inc.,1998:151-190.
[9] Nedeljkov M,Oberguggenberger M.Interactions of delta shock waves in a strictly hyperbolic system of conservation laws[J] .Journal of Mathematical Analysis and Applications,2008,344(2):1143-1157.
[10] Shen Chun,Sun M.Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model[J] .Journal of Differential Equations,2010,249(12):3024-3051.
[11] Tan D C,Zhang T,Chang T,et al.Delta-shock waves as limits of vanishing viscosity for hyperbolic system of conservation laws[J] .Journal of Differential Equations,1994,112(1):1-32.
[12] Wang Zhen,Zhang Qingling.The Riemann problem with delta initial data for the one-diemensional Chaplygin gas equations[J] .Acta Mathematica Scientia,2012,3(2):825-841.
[13] Shen Chun,Sun M.Interactions of delta shock waves for the transport equations with split delta functions[J] .Journal Mathematical Analysis and Applications,2009,351(2):747-755.

