量子遗传算法在多元函数优化上的应用

梅晓娟， 徐余法， 苏强强， 戴志军

（上海电机学院 电气学院，上海200240）

随着智能算法的广泛使用，复杂函数的优化问题也得到了广泛的重视。遗传算法（Genetic Algorithm，GA）是函数优化中应用最广泛的智能算法。20世纪40年代起，有学者利用计算机进行生物模拟的研究[1]。GA是一类借鉴生物界的自然进化规律演化而来的随机化搜索方法，具有较好的全局寻优能力，通过优胜劣汰的选择，使得算法能够向着最优解的方向进行。在实际应用过程中，GA也暴露出了很多缺点，如早熟、对初始种群的选择依赖性大、寻优速度慢、并行性较差等[2-3]。

为了解决GA存在的不足，科学家提出将蚁群算法 与 GA 的 结 合[2，4-5]，以 提 高 GA 的 寻 优 速度；有学者提出将粒子群算法与GA相结合[6]以提高精度等。近年来，量子算法凭着其独有的相干性和并行性，已得到了学者们的青睐。因此，学者们也把量子算法与GA进行组合，充分利用它们的优势，使得其应用更加广泛。目前，量子遗传算法（Quantum Genetic Algorithm，QGA）在组合优化、函数优化、信号处理等方面得到了应用，并取得了良好效果[7]。本文就多元函数的优化问题，证明了QGA比传统GA在精度、寻优速度、收敛性等方面都要好。

1 量子算法基本概念

19世纪初，科学家提出了量子力学理论；量子独有的相干性和纠缠性等特性为量子计算带来了不同于经典计算的独特运算方式[8]。近年来，量子算法得到了快速发展，并取得了一系列惊人成就。目前，应用广泛的量子算法主要有Shor大数质因子分解算法、Grover数据库搜索算法。Shor大数质因子分解算法实现了算法的量子编码，并且成功地证明了难解的NP问题可以在多项式时间内完成[9]。Grover算法适于解决在无序数据库中搜索一个特定的问题。由于量子算法的并行性，故Grover算法每次可以同时查找所有的数据，大大提高了寻找的速度和概率[8]。在Shor算法和Grover算法后，量子智能算法引起了研究者们更大的兴趣，QGA是量子智能算法之一。目前，其研究主要集中在组合优化、数值优化等有限的领域，还有待开拓更广阔的领域，现在已有学者将量子算法用于机器人的控制中[10-11]。随着科技信息的快速发展，人们对获取信息的速度要求越来越高，因此，量子算法独有的并行性将会得到更好的应用，其混合应用也会越来越多，如理论上，QGA可以应用于传统GA所应用的领域，但目前其应用领域较少。因此，QGA必将向着更广的领域发展。

1.1 量子比特

量子计算中的基本单位是量子位或量子比特（qubit），用｜0〉和｜1〉表示（其中“｜〉”是量子力学中表示量子状态的符号，称为Dirac符号）[8]。与经典计算机中的bit不同的是：qubit可以为任意归一化的态，即由｜0〉、｜1〉两个基本比特单位叠加而成的叠加态，可表示为式中，α、β为相应状态的概率幅，均为复数，且满足归一化条件：｜α｜2＋｜β｜2＝1。

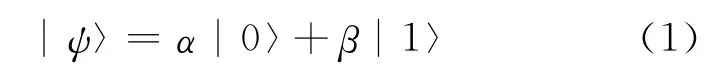
如，在经典计算机中，需要用00、01、10、11表示4种不同的信息，且存储器每次只能记录一种状态。但在量子计算中，量子存储器可以一次以量子叠加态的形式存储这4个不同的状态。也就是说，对于相同维数的存储器，量子计算机可以处理的信息量是经典计算机的指数倍。对于一个n量子位的存储器，它可以同时存储2n个不同的数字，且这2n个不同的数字是用同一个量子态表示的，其一般表示形式[8，12]为

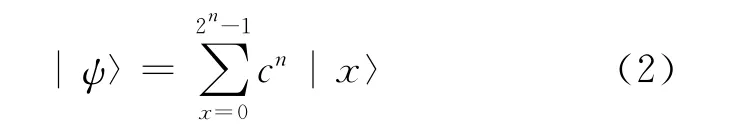
式中，x为由基本比特单位叠加而成的任意位的量子比特；c为x的位数，如x由基本比特｜0〉、｜1〉叠加代表了4种状态，则c＝4。

1.2 量子逻辑门

量子计算中，基本的操作单元叫做量子逻辑门，简称量子门。量子门由幺正矩阵或幺正矩阵的组合构成，通过对量子态实施幺正操控实现对信息的逻辑变换[8]。根据输入比特个数的不同，量子门可分为单比特、二比特以及多比特逻辑门。有研究表明[13]，任何复杂的幺正变化最终都可以分解为简单的量子门来实现。因此，量子逻辑门的实现最关键的是一位和两位量子门的实现[14]。如

式中，P（θ）为一个幺正操作，且该幺正操作就是一个单比特的逻辑门，即单比特门；θ＝k·f（α，β），为旋转角，其中，k＝5exp（-t／100），t为遗传代数；eiθ＝[cosθsinθ] ，i为复数单位。

两位量子逻辑门有两个相互作用的量子位：控制位和目标位。控制位在门操作后保持不变，但其状态决定了目标位的演化。如果控制位是｜0〉，则目标位不发生任何改变；如果控制位是｜1〉，则目标位将经历一个确定的变换。其他位的量子门的操作由1、2位的组合构成[13]。

2 量子遗传算法（QGA）

QGA是量子计算和GA相结合的产物。目前，对该领域的研究主要集中在两个方面：①基于遗传理论的量子算法；② 基于量子理论的遗传算法。前者是将量子的态矢量表达应用到遗传编码中，利用量子旋转门来实现染色体的演化；后者在于利用量子的并行搜索原理，扩大搜索范围，利用量子的相干性，实现信息间的交流，从而整体上提高算法的搜索效率，因此，本质上其仍属于GA范畴。本文应用的QGA中，一个染色体即包含所有可能的解，真正融合了量子算法与传统GA的优点[13]。

2.1 量子编码

所谓的量子编码就是用量子基本态以及量子的组合态来代替遗传编码中的0、1组合所表示出的信息[15]。如在经典编码中要用0、1来表示4个信息，并且要向计算机传送4个0、1串才能表达出4个信息；但在量子中，仅需要用｜0〉、｜1〉两个基本态以及它们的组合态｜ψ〉＝α｜0〉＋β｜1〉即可，通过调整α、β的大小就可以表达不同的信息。

2.2 量子变异

在量子算法中，对一个染色体的任何操作，也是同时对其所在的整个解空间进行操作。因此，它对所有的解具有相同的意义，也就是说在QGA中交叉没有意义。文献[8] 中引入了量子变异操作，来改变QGA的性能。其单比特量子门的变异方法如下。

（1）对每一代的个体随机确定一个变异位，类似于传统GA的变异位的选择。

（2）将该量子位的系数（αi，βi）位置互换，即完成了量子变异的操作。

如对该染色体的第6位进行变异，通过调整（αi，βi）的位置即可，则变异前 ｜0〉｜1〉｜1〉｜1〉｜1〉｜1〉｜0〉｜0〉变异后 ｜0〉｜1〉｜1〉｜1〉｜1〉｜0〉｜0〉｜0〉

类似的方法可推广到多量子比特的情况。

2.3 基本步骤

QGA的基本步骤如下[14]：

（1）初始化种群p（t），随机生成n个以量子比特为编码的染色体，本文选择初始值为

（2）对p（t）中的每个个体进行一次测量，得到对应的确定值；

（3）对每个确定值进行适应度评估，记录最优个体以及对应的适应值；

（4）判断计算过程是否满足条件，即是否达到全局的最优值，若满足条件，则计算结束；否则继续；

（5）利用量子旋转门U（t）对个体进行调整，得到一个新的种群p（t＋1）；

（6）令t＝t＋1，并返回步骤（2）。

3 实例分析

为证明QGA的性能，本文选择文献[15] 中的一个二元函数进行验证，该函数为

约束条件为

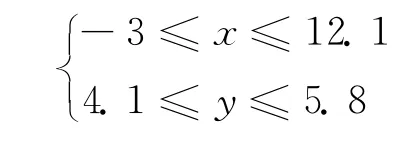
求解该二元函数的最小值。

在传统GA中，各变量初始值如下：种群规模为50，染色体基因位为18，交叉概率为0.7，变异概率为0.05。

图1、2给出了利用GA和QGA分别迭代200次和1 000次的寻优结果。

由图1可知，利用GA迭代200次得到的f（x，y）的最小值为-16.640 0；迭代1 000次得到f（x，y）的最小值为-17.409 7。由图2可知，利用QGA迭代200次得到f（x，y）的最小值为-17.115 1，其中x1＝11.369 7，x2＝5.775 69；迭代1 000次得到f（x，y）的最小值为-17.258 2，其中，x1＝11.863 3，x2＝5.671 35。

由仿真结果可见，当迭代200次时，GA需要约60代才能达到稳定最优值-16.640 0，而QGA仅需约15代即可达到最优值-17.115 1。由此可见，在寻优速度上，QGA要优于GA。当迭代次数为1 000次时，随着迭代次数的增加，GA的精度有了明显的提高，但寻优速度却明显下降；而QGA的寻优速度及精度几乎没有变化，由此可见，QGA与迭代次数的多少关系不大。因此QGA的寻优速度及精度都是要优于传统的GA。

图1 GA寻优的仿真结果Fig.1 Simulation results of GA optimization

图2 利用QGA寻优的仿真结果Fig.2 Simulation results of QGA optimization

4 结 语

QGA是量子计算与遗传算法相结合的产物。本文简单介绍了量子算法、QGA的基础理论，并利用Matlab验证了QGA在解决多元函数优化问题上的优势。量子算法是一种较新的理论，在很多方面还不很成熟。其理论研究主要是在构造新的量子门等方面，对于算法收敛性、收敛速度估计、参数设置对算法的影响等的研究还很少涉及，还有待于进一步研究。

[1] 朱文龙.基于遗传算法的BP神经网络在多目标优化中的应用研究[D] .哈尔滨：哈尔滨理工大学，2009：18-30.

[2] 王雅芳.遗传算法结合蚁群算法电力系统故障浅析[J] .系统仿真技术，2008，4（1）：56-60.

[3] Patalia，T P Kulkarni G R.Behavioral analysis of genetic algorithm for function optimization[C] ∥2010IEEE International Conference on Computational Intelligence and Computing Research（ICCIC）.Coimbatore：IEEE，2010：1-5.

[4] 高尚，江新姿，汤可宗.蚁群算法与遗传算法的混合算法[C] ∥Proceeding of the 26th Chinese Control Conference.Zhangjiajie：IEEE，2007：701-104.

[5] Wei Juan，Wang Ping.Optimization of fuzzy rule based on adaptive genetic algorithm and ant colony algorithm[C] ∥2010International Conference on Computational and Information Sciences.Chendu：IEEE，2010：359-362.

[6] 巩永光.粒子群算法与遗传算法的结合研究[J] .济宁学院学报，2008，29（6）：20-22.

[7] 梁昌勇，柏桦，蔡美菊，等.量子遗传算法研究进展[J] .计算机应用研究，2012，29（7）：2401-2405.

[8] 林家逖，任德龙，田欣，等.经典逻辑门与量子逻辑门之比较[J] .计算机工程与科学，2005，27（11）：93-95.

[9] 王凌.量子进化算法研究进展[J] .控制与决策，2008，23（12）：1321-1326.

[10] Shill P C，Amin M F，Akhand M A H，et al.Optimization of interval type-2fuzzy logic controller using quantum genetic algorithms[C] ∥International Conference of Fuzzy Systems.Brisbane，QLD：IEEE，2012：1-8.

[11] Bennett CH，Brassard G，Crepeau C，et al.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J] .Physical Review Letters，1993，70（13）：1895-1899.

[12] 王蕴，黄德才，俞攸红.量子计算及量子算法研究进展[J] .计算机系统应用，2011，20（6）：228-231.

[13] 熊焰，陈欢欢，苗付友，等.一种解决组合优化问题的量子遗传算法 QGA[J] .电子学报，2004，32（11）：1855-1858.

[14] 王凌，吴昊，郑大忠，等.混合量子遗传算法及其性能分析[J] .控制与决策，2005，20（2）：156-159.

[15] 史峰，王辉，胡斐，等.MATLAB智能算法30个案例分析[M] .北京：北京航空航天大学，2011：79-87.