三轴运动加速度计（GT3X）测量青春期少年（11～14岁）身体活动能耗预测方程的建立和检验

朱 琳，陈佩杰

1 前言

Physical Activity即身体活动，也有人将其译为体力活动，是指由骨骼肌收缩产生的、使能量消耗增加的身体动作。身体活动与人体健康密切相关[14]，身体活动能量消耗是引起总能量消耗变化的最大可变成分[10]。因此，准确测量身体活动能耗不仅可以了解该人群身体活动水平，有的放矢地指导其科学运动，也可为制定膳食推荐标准提供支持。那么，解决问题的关键是找到一种行之有效的身体活动测量方法。目前，日常体力活动监测中常用的能耗监测方法有运动加速度计和问卷法等。问卷法虽然简便易行，但报告往往被限制在一定范围的活动种类上，而活动种类往往不能准确区分活动的不同强度；其次，报告者的年龄对问卷测试的准确性有一定的影响，使问卷法的准确性和适用范围具有一定的局限性。运动加速度计是基于牛顿力学定律，通过测量身体加速度绝对值的积分，通过身体运动的持续时间和强度的测量对身体活动提供客观的评估，具有较高的信度和效度；运动加速度计因其可在不干扰受试者正常活动的情况下长时间佩戴，是目前科研人员常见的身体活动监测和评估手段，其中，三轴运动加速度计因其可同时测量人体在垂直轴、冠状轴和矢状轴三个方向上身体活动的加速度变化，更能准确地反映人体的真实运动。然而，运动加速度计是通过预测方程来实现能耗监测，现有的预测方程多是国外学者针对当地成年人，以走、跑运动为基础建立的[9，12]，使预测方程对人群或活动的适用范围和适用广度具有一定的局限性。为此本研究针对青春期少年建立基于走跑与非走跑运动为基础的三轴运动加速计能耗预测方程。

2 研究对象和研究方法

2.1 研究对象

研究招募80名11～14岁初中生（每岁20人，男女各半）按性别、年龄分成实验组（60人）和验证组（20人）；实验组用于方程的建立，验证组用于方程的检验。所有参加者均身体健康，没有参与过系统的运动训练（表1）。

表1 本研究受试者基本信息一览表Table1Descriptive Characteristics of Subjects ±S）

表1 本研究受试者基本信息一览表Table1Descriptive Characteristics of Subjects ±S）

实验组GroupE验证组Croup Ctr男性（n＝30） 女性（n＝30） 男性（n＝10） 女性（n＝10）年龄（yr） 12.91±0.96 12.95±0.98 13.14±0.91 13.04±0.96身高（m） 1.63±0.10 1.57±0.05 1.65±0.05 1.56±0.06体重（kg） 56.45±12.34 49.42±9.73 54.52±7.36 48.94±5.75 BMI（kg/m2） 21.05±3.55 19.87±2.93 19.99±2.32 20.26±2.84

2.2 研究方法

2.2.1 测试安排

第一部分非走跑活动测试，运用Cosmed K4b2（以下简称K4b2）和三轴运动加速度计ActiGraph GT3X（以下简称GT3X）对受试者进行第三套全国中学生广播操（舞动青春）和1min尽力跳绳测试，两项测试后均要求受试坐位休息至恢复；第二部分实验室跑台走跑运动递增负荷测试，餐后1h以上运用K4b2和GT3X同步监测3～6km/h走和7～8km/h跑的运动，每级运动5min，跑台坡度为0，中间无休息（表2）。

2.2.2 Cosmed K4b2便携式气体代谢分析仪

间接测热法所设计的间接能量测定仪是测定机体能量消耗的“金标准”[3，4]，K4b2（Cosmed，Rome，Italy）是利用间接测热原理，通过分析每一口气中氧和二氧化碳的含量，计算单位时间能量消耗，现已证实其可有效测量各种运动强度下的摄氧量[13]。实验测试过程，严格按照操作手册进行，通过随机配备的数据分析处理系统导出数据表，并提 取 能 耗 参 数O2（ml/min）、CO2（ml/min），通 过WEIR公式计算能耗[5]。各运动项目的能耗参数提取方法为：广播操选择整个活动时间；1min尽力跳绳，考虑到此运动会产生运动后过量氧耗的问题，跳绳＝（跳绳期平均值＋恢复期平均值×恢复时间）/运动时间[1]；跑台走、跑递增负荷运动选取每级运动的后2min的稳态期数据，第1～3min作为平衡期。跳绳恢复及走跑稳态的标志是HR和O2的宽容度分别在±5BPM和±10%[5，6]的范围内。

2.2.3 ActiGraph GT3X三轴运动加速度计

本研究采用60s时间间隔采样模式，三轴测试方式；在部分实验开始，GT3X要依据制造商的说明书被初始化，并将仪器通过一个尼龙弹性腰带固定在右腋窝中线和髂嵴水平线的交界处[13]。实验后可以通过自带数据分析软件ActiLife 5导出EXCEL数据表，提取原始指标垂直轴活动计数（ACxis1）、冠状轴活动计数（ACxis2）、矢状轴活动计数（ACxis3）、三轴向量幅值 VM3（Vector Magnitude，VM），VM3＝（ACxis12＋ACxis22＋ACxis32）1/2。

表2 本研究实验的测试方案一览表Table2 Test Scheme

2.2.4 数据简化

2.2.5 数据的统计处理

通过实验组运用逐步回归方法建立回归方程。通过验证组针对日常活动类、走跑类、走跑跳类、不规则活动类等四种活动类型对所建方程进行验证；绝对误差＝∑｜实测值－方程预测值｜/n和相对误差率＝｜实测值－方程预测值｜/实测值×100%用于验证方程预测准确性；Bland－Altman图用于确定方程的系统偏差；P＜0.05为有统计学意义。统计分析均用EXCEL 2007和SPSS 16.0完成。

3 研究结果

3.1 GT3X能量消耗预测方程的建立

通过实验组以K4b2实测能耗值为因变量，以ACxis1、ACxis2、ACxis3、VM3、年龄、性别、身高、体重等为自变量，获得回归方程 Y（Kcal/min）＝－1.471＋0.10440×体重（kg）＋6.15209E－4×VM3（counts/min）。方程的R2＝0.703，SEE＝0.82，F检验P＜0.001，说明自变量与因变量存在线性关系，方程的拟合程度较高；自变量回归系数和常数项t检验，P＜0.05，说明自变量回归系数和常数项有意义；Durbin－Watson（以下简称DW）统计量通过确定两个相邻误差项的相关性是否为零来检验回归残差是否存在自相关，DW越接近2表明判断误差项无自相关性的把握越大，本研究所建方程的DW 为1.734，查Durbin－Watson Test检验表，方程DW值满足UD＜DW＜4－UD，残差不存在一阶正自相关，表明方程误差项独立，回归模型可靠。

3.2 能耗预测方程的验证

因考虑到所建方程在今后的能耗评估中，主要是用于日常生活身体活动的能耗监测，而日常身体活动的形式是多样的，如果只是对单项身体活动进行验证显然是不合理的，为此研究将活动分成不同活动类型进行方程的检验。通过验证组，运用所建回归方程对四种类型活动的能耗预测能力进行检验，以验证本研究建立的能量消耗预测方程的有效性（表3）。

从表3可知，对于四类活动方程预测绝对误差在0.58～0.63kcal/min之间，相对误差率为9.14%～11.81%；经Bland－Altman散点图分析（图1），实测值与预测值95%的残差均落在Bland－Altman散点图±2SD区间内，表明方程对四类活动均有较好的预测能力。

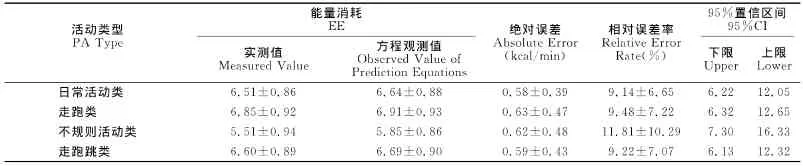
表3 本研究能耗预测方程对不同活动类型能耗的预测一览表Table3 Observation Capabilities of Energy Expedition Prediction Equations Monitoring Four PA Types

图1 本研究所建预测方程对四种类型活动预测的Bland－Altman散点图Figure1.Bland–Altman Plots of the Paper’s Energy Expedition Prediction Equations for Monitoring Four PA Types

4 分析与讨论

在实际的日常生活中，人们的主要活动形式可归为走、跑、跳，而走、跑是最为常见的活动形式，其中，极低速的走或极快速的跑在日常生活中均少见[2]；同时，由于日常活动通常以垂直轴和水平面的活动情况较多，因此，运动加速度计特别是GT3X等三轴运动加速度计在评价日常身体活动能耗方面具有一定的优势，建立其相应的能耗预测方程也更有意义。

对于自由活动状态的受试者，运动加速度计是一种能够描述身体活动模式的有效工具。以运动加速度计预测能量消耗（EE）的验证性研究主要是在短期的实验室或模拟自由生活的状态下进行的实验[11]。GT3X官方软件中的五个能耗预测公式适用于19岁以上成年人，因此，本研究以EE为因变量来建立基于走跑与非走跑运动为基础的适用于青春期少年日常身体活动的能耗预测方程。

本研究以 EE为因变量，以 ACxis1、ACxis2、ACxis3、VM3、年龄、性别、身高、体重为自变量进行逐步回归分析，结果VM3和体重进入最终方程。这表示VM3和体重比ACxis1、ACxis2、ACxis3、年龄、性别、身高等信息更能反映因变量，说明EE与VM3和体重存在线性关系；所建方程R2＝0.703，说明因变量的70.3%的变异可以由VM3和体重解释，方程的拟合程度较高；且DW接近2，表示回归方程有效，回归模型可靠。

儿童青少年的身体活动往往是复杂的和不规律的活动，而不是单纯的走或跑或跳等运动，因此，本研究将活动分为四种活动类型对方程的预测能力进行检验。研究显示，所建预测方程对日常活动类、走跑类、不规则活动类、走跑跳类等四种活动类型的预测绝对误差分别为0.58 kcal/min、0.63kcal/min、0.62kcal/min、0.59kcal/min；对日常活动类（9.14%）、走跑跳类（9.48%）、不规则活动类（11.81%）和走跑跳类（9.22%）活动的预测相对误差均在15%以内外，准确度均在85%以上。Bland－Altman方法的目的是计算出两种测量结果的一致性界限，并以图形的方式直观地反映出这种一致性界限，以得出这两种测量方法是否具有一致性的结论；Bland－Altman散点图显示，对于四种活动类型的运动，95%的预测值与实测值的残差均在±2SD以内，说明方程具有较好的预测能力，能有效预测日常生活中的各种类型活动。

有研究者[13]在儿童青少年中同时评估三个能耗预测方程，研究者通过45个年龄在10～18岁的儿童青少年受试者运用GT3单轴运动加速度计和Cosmed K4b2对Trost、Freedson和Puyau equations这3个能耗预测方程的有效性进行了研究，其方法是让参与者在室外平坦的大椭圆行跑道内以正常步速走（5.052km/h），轻快步速走（6.708km/h），慢跑（10.074km/h），快跑（12.804km/h）等4种方式进行运动，每个速度运动5min。理想情况下，一个运动加速度计的预测方程应该可以准确地预测一系列活动类型的能量消耗和运动强度，但他们的研究显示，没有一个方程能在4个活动实验中准确地预测平均能耗。这些发现也再一次说明，运动加速度计在被用于监测儿童青少年等比较活跃的受试者的身体活动与日常身体活动能耗监测之前，额外的校正研究是必要的。

GT3X基于每分钟垂直轴活动计数建立的能耗预测方程对预测低、中等运动强度的身体活动能量消耗是一个很好的测量工具，然而它却不能精确地评估高强度运动的身体活动能量消耗，这是单轴和三轴运动加速度计的一个普遍公认的缺陷[7，8，12]，其主要原因是高强度活动时垂直轴AC会出现平台期，换句话说它只能判断一定加速度阈值之下的运动，而对于超过这个阈值的运动不能加以区分。以往能量消耗预测方程的建立多是基于实验室或自由状态下的走、跑等活动形式，而现实生活中的活动往往是多样化的，特别是儿童青少年的活动种类更是多样化。本研究在走、跑的基本运动形式中加入跳、广播体操等不规则活动，对提高方程预测日常身体活动能耗的准确性方面具有一定的实用价值。本研究所建方程是通过活动计数和体重来预测能量消耗的，因此，即包括了身体的信息，也包括了运动的信息。GT3X运动加速度计可以自由选择单轴、双轴和三轴的测试模式，虽然在多数活动中常以垂直轴的活动占优势，但日常活动中复杂的空间活动更为常见，因此使用向量幅值更能准确地反映日常活动的真实情况，对于预测身体活动能量消耗也更加准确。

5 结论

本研究应用线性回归分析的方法，建立的以三轴向量幅值和体重为自变量的能耗预测方程有效，能有效监测11～14岁青春期少年不同活动类型的能耗，适用于对青春期少年的日常身体活动的能耗监测。

[1]陈吉棣.运动营养学[M].北京：北京医科大学出版社，2002：15.

[2]戴剑松，孙飙，沈洪兵.加速度传感器测量体力活动的应用综述[J].中国运动医学杂志，2009，（6）：720－727.

[3]孟庆华，冯岩梅.静息能量消耗测定在慢性肝病中的应用[J].中国临床营养杂志，2007，15（2）：107－110.

[4]朱琳，陈佩杰.能量消耗测量方法及其应用[J].中国运动医学杂志，2011，30（6）：577－582.

[5]朱琳，陈佩杰，庄洁，等.12～14岁正常和肥胖男性青少年运动能耗的比较研究[J].中国运动医学杂志，2011，30（2）：166－169，181.

[6]ARVIDSSON D，SlINDE F，LARSSON S，etal.Energy cost of physical activities in children：validation of SenseWear Armband[J].Med Sci Sports Exe，2007，39（11）：2076－2084.

[7]BRAGE S，WEDDERKOPP N，FRANKS P W，etal.Reexamination of validity and reliability of the CSA monitor in walking and running[J].Med Sci Sports Exe，2003，35（8）：1447－1454.

[8]KING G A，TORRES N，POTTER C，etal.Comparison of activity monitors to estimate energy cost of treadmill exercise[J].Med Sci Sports Exe，2004，36（7）：1244－1251.

[9]MATTEWS C E，AINSWORTH B E，THOMPSON R W，etal.Sources of variance in daily physical activity levels as measured by an accelerometer[J].Med Sci Sports Exe，2002，34（8）：1376－1381.

[10]NILSSON A，BRAGE S，RIDDOCH C，etal.Comparison of equations for predicting energy expenditure from accelerometer counts in children[J].Scand J Med Sci Sports，2008，18（5）：643－650.

[11]ROTHNEY M P，SCHAEFER E V，NEUMANN M M，etal.Validity of physical activity intensity predictions by ActiGraph，Actical，and RT3accelerometers[J].Obesity （Silver Spring），2008，16（8）：1946－1952.

[12]SASAKI J E，JOHN D，FREEDSON P S.Validation and comparison of ActiGraph activity monitors[J].J Sci Med Sport，2011，14（5）：411－416.

[13]TROST S G，WAY R，OKELY A D.Predictive validity of three ActiGraph energy expenditure equations for children[J].Med Sci Sports Exe，2006，38（2）：380－387.

[14]US.DEPARTMENT OF HEALTH AND HUMAN SERVICES.Physical activity and health：a report of the surgeon general[M].International Medical Publishing，1996：85－142，29.