基于时变自回归模型的非平稳数据预测方法研究
王莉娜,姜相夺,芦玉华
基于时变自回归模型的非平稳数据预测方法研究
王莉娜,姜相夺,芦玉华
针对现有的自回归(Autoregressive, AR)模型对非平稳数据预测效果不佳的问题,提出了基于时变自回归(Time-Varying Autoregressive, TVAR)模型的时序预测方法。针对某型国产飞机发动机的低压转速信号,使用TVAR模型分别进行点预测和区间预测,并与AR模型的点预测结果进行对比。研究结果表明,TVAR模型能够很好地反映非平稳数据的变化趋势。在给定置信水平下,TVAR预测区间能够包含真实数据,因此TVAR模型在时序预测中具有更好的预测效果。
时间序列;时变自回归模型;预测
0 引言
近年来,随着微机、航空、航天、电子、通信金融等领域的发展,时间序列预测变得越来越重要,是当前科学研究的热点之一。目前,我国学者已将时间序列法中的回归分析法、分解分析法应用于故障率预测,然而回归分析法需要首先识别目前产品所处阶段,分解分析法则需要大量数据支撑,不适用于数据量少的情况,这两种方法都存在一定的局限性。时间序列法中的ARMA(Autoregressive Moving Average)模型能较好地解决上述问题,无须识别产品所处阶段,所需数据量少,且预测精度较高,便于在线性最小方差意义下进行最佳预报和控制。研究人员已经将ARMA模型应用于故障数预测、设备缺陷数预测[1][2]。
ARMA模型的两种特殊情况是AR模型、MA模型等。其中,由于AR模型的结构相对简单,在某种意义上,AR模型和MA模型及ARMA模型可以相互转化,因此AR模型的应用范围最广。AR模型的系数是常数,不能随着信号的变化而不断调整,适用于平稳信号,对非平稳信号的适用性较差。
TVAR模型是将AR模型的常系数ai展开为一组基时间函数的线性组合,模型系数能够动态调整,可以更好地描述信号的变化,已经在模态识别[3],语音分析[4]及故障诊断[5]等方面成功应用。
本文针对TVAR模型在非平稳信号处理方面的优势,提出了基于TVAR模型的非平稳数据预测方法。
1 时变自回归模型
1.1 AR预测模型简介
AR模型是一种特殊的随机线性时不变(LTI)系统离散时间模型。该模型的输出序列y(n)可以看作是白噪声e(n)通过有理滤波器得到。对于长度为N的时间序列y(n),其AR模型具有如下形式:
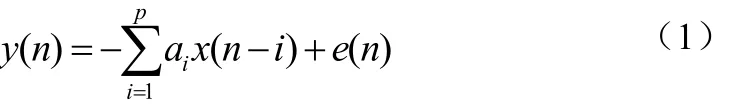
其中,y(n)为第n时刻的采样值,ai为AR模型的系数,p为模型的阶数,e(n)为模型的残差。
假设要对长度为N的时间序列y(n)作k步预测,设第n时刻的预测值用yˆ(n)表示,则第N+k时刻的预测数据有如下形式如公式(2):
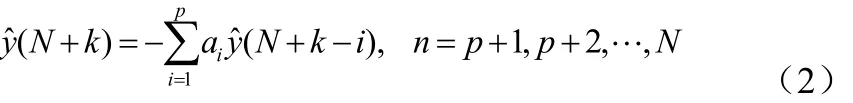
1.2 TVAR预测模型
(1)点预测
TVAR模型是将AR模型的常系数ai展开为一组基时间函数的线性组合,因此该模型能够根据信号的变化而不断地调整模型的系数,从而能够更好地描述信号的变化,即对于长度为N的时间序列y(n),TVAR模型用差分方程形式表示如公式(3)、(4):
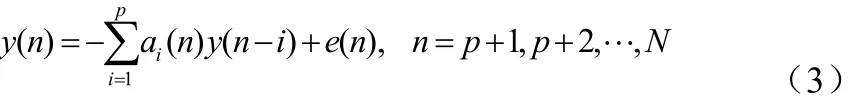

其中,y(n)为第n时刻的采样值,ai(n)为时变系数,p为模型的阶数,e(n)为模型的残差,aij为基时间函数的加权系数,gj(n)为基时间函数,m为基展开的维数。
假设要对长度为N的时间序列y(n)作k步预测,即使用有限个历史数据y(1),y(2),…,y(N)对第N+k时刻的数据y(N+k)作预测,设第n时刻的预测值用yˆ(n)表示,则第N+k 时刻的预测数据有如下形式如公式(5):
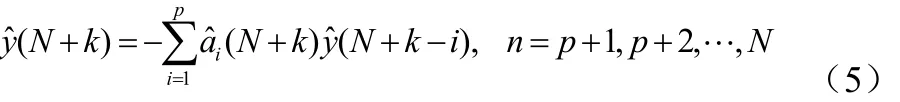
其中,当i≥k时,yˆ(N+k−i )=y(N+k−i )。
使用文献[7]所用的前后向估计相结合的方法估算出系数aij以后,便可使用公式(4)计算出aˆi(N+k)的值,之后利用公式(5)便可计算出第N+k时刻的预测值yˆ(N+k)。
2 区间预测
在参数的点估计中,当θˆ=θˆ(X1,X2,…,Xn)是未知参数θ的一个估计量时,对于一组样本值(x1,x2,…,xn)就得到θ的一个估计值θˆ=θˆ(x1,x2,…,xn)。点估计就是取θ≈θˆ,这使得我们对θ的值有了一个明确的数量概念。但是,点估计值θˆ仅仅是未知参数θ的一个近似值,这种近似值的精确程度或误差范围都没有给出,这是点估计的缺陷,而区间估计则正好在一定程度上弥补了点估计的这个缺陷[8]。
y(N+k)的第k步预测由式(5)给出,则第k步预测的方差由公式(6)给出:
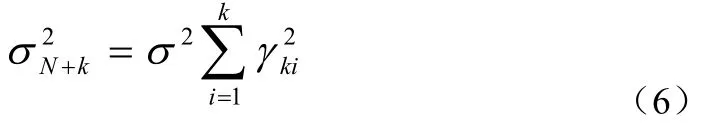
其中如公式(7):
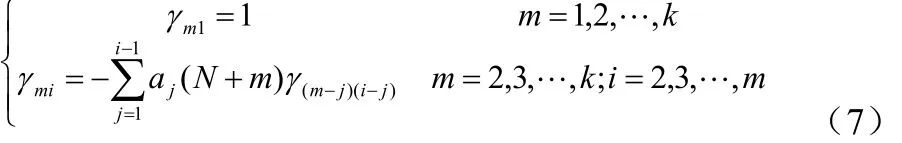
当i>p时,ai(n)=0,σ2为前N时刻的方差。
于是y(N+k)的置信水平为1−α的置信区间如公式(8):
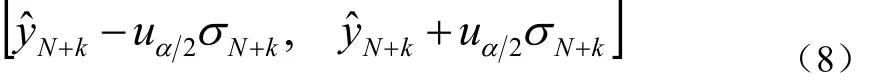
公式(6)至公式(8)的具体推导过程参见文献[9]。
3 点预测算例分析
为了探讨TVAR算法的预测效果,本文选用某型国产飞机发动机所采集到的左发低压转速NL为预测对象。选取其中的528个数据点,前508个数据点作为历史数据,后20个数据点为待预测数据。模型阶数的选取采用AIC预报准则[10],TVAR模型选用DCT基时间函数(Discrete Cosine Transform)[11],基展开维数为12。
为了更清楚地查看AR模型与TVAR模型的预测效果,将真实值与预测值作图比较。真实的528个数据点的波形图,如图1所示:
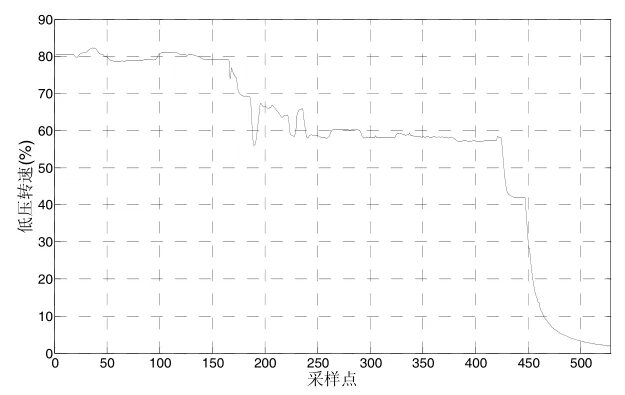
图1 低压转速时间序列
由图1可知,所选取的508个历史数据变化比较大,尤其是在第160个数据点和第420个数据点时,数据下降得比较剧烈,而所需预测的最后20个数据点已经趋于平缓。AR模型的预测结果,如图2所示:
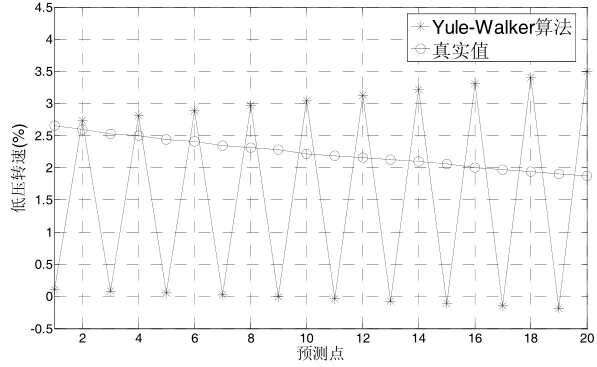
(a) Yule-Walker算法
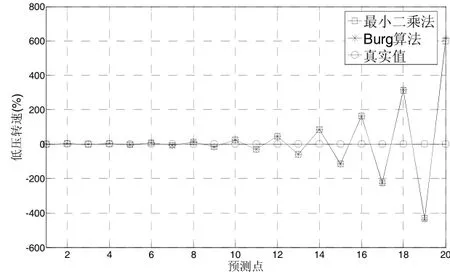
(b)最小二乘与Burg算法图2 AR模型预测
AR系数估计方法包括Yule-Walker算法,最小二乘算法和Burg算法。为了有一个更清晰的比较,将Yule-Walker算法单独作图,如图2(a)所示,从图中可以看出,使用Yule-Walker算法所预测的数据与真实值存在较大误差,且围绕真实值上下波动,并不能体现出后20个点的变化趋势。图2(b)为使用Burg算法与最小二乘方法预测的结果。从图中可以看出,最小二乘方法与Burg算法所预测的数据有相似的预测结果和相同的变化趋势,二者的预测值均围绕着真实值上下波动,但是预测的数据逐渐发散,预测误差越来越大。由此可见,使用Yule-Walker算法,最小二乘算法和Burg算法等3种方法进行AR模型的系数估计,所预测的数据并不能很好地反映真实数据的变化趋势,且预测误差逐渐增加。
为使用TVAR模型所得到的预测结果如图3所示:
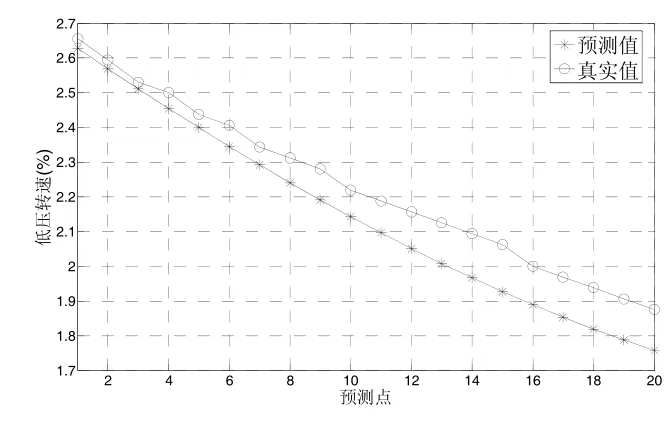
图3 TVAR模型预测
从图中可以看出,TVAR模型的预测数据与真实的低压转速之间的差别很小,虽然随着预测步长的增加,预测的误差逐渐增大,但是该模型基本能够较好地反映真实数据的变化趋势,且预测误差也在允许的范围以内。
4 区间预测算例分析
为了研究预测值的估计精度与误差范围,对第3节的发动机低压转速进行区间估计。选取α=0.10,即置信水平为90%,查看正态分布表可知,此时,利用公式(6)至公式(8)计算第k步预测的真实值y(N+k)的置信区间,TVAR模型区间估计的结果,如图4所示:
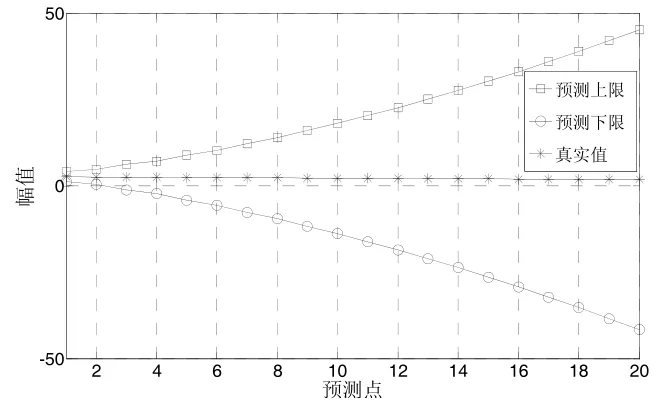
图4 TVAR模型区间估计
从图4可以看出,所预测的20个真实值全都落在预测区间中,然而,随着预测步长的增加,预测的区间半径逐渐增大,这是因为由于累积误差的存在,预测值与真实值的差距越来越大,为了保证预测结果的可靠性,必然得增加预测区间的长度,因而预测的精确度有所降低。
由此可见,对于区间预测来说,预测的可靠度与精确度是相互制约的。在实际应用中,常采用一种折中的方案,在使得置信度达到一定要求的前提下,寻找精确度尽可能高的区间估计。实际上,对于本例来说,由于所预测的发动机低压转速不可能为负值,所以从第3个预测点开始,预测下限就已经不具有物理意义了。
5 总结
本文主要研究了TVAR模型在时序预测方面的应用。针对比较常见的预测类型——点预测与区间预测,分别推导了TVAR预测模型的公式。通过对某型国产飞机在某次飞行中的发动机低压转速的一段数据,使用TVAR模型与AR模型进行步长为20的点预测和区间预测,结果表明,对于变化比较大的数据,AR模型并不能很好地跟踪信号的变化趋势,甚至会出现非常大的预测误差。而TVAR模型的能够很好地反映真实数据的变化趋势,且预测误差也在允许的范围以内。在给定置信水平下,TVAR预测区间能够包含真实的数据,因此具有更好的预测效果。
[1] 李瑞莹,康锐.基于ARMA模型的故障率预测方法研究[J].系统工程与电子技术,2008,30(8):1588-1591
[2] 王治华,傅惠民. 广义时变ARMA序列预测方法[J]. 航空动力学报,2005,20(5):713-717
[3] 续秀忠,张志宜,华宏星等.应用时变参数建模方法辨识时变模态参数[J].航空学报,2003,24(3):230-233
[4] 朱志宇. 基于高斯粒子滤波器和TVAR模型的语音增强技术[J].仪器仪表学报,2008,29(9):1903-1907
[5] 熊国良,张龙,陈慧.TVAR在非平稳工况转子故障诊断中的应用[J].振动、测试与诊断,2007,27(2):108-111
[6] Petre Stoica, Randolph Moses著,吴仁彪,韩萍,冯青,等译.现代信号谱分析[M].北京,电子工业出版社,2007
[7] 芦玉华 ,王仲生,姜洪开.基于改进时变自回归模型的滚动轴承故障诊断 [J]. 振动与冲击,2011,30(12):74-77,107
[8] 徐伟,赵选民,师义民,等. 概率论与数理统计[M]. 西安,西北工业大学出版社,2005
[9] 王永民,何幼桦,忻莉莉,等. 时变自回归模型系数的估计及预测[J]. 应用数学与计算数学学报,2007,21(2): 35-41
[10] 杨俊岭,张长隆,万建伟. 基于信息量准则的AR模型相关高斯杂波模拟[J]. 航天电子对抗,2006,22(2):45-48
[11] Kie B.Eom. Analysis of Acoustic Signatures from Moving Vehicles Using Time-Varying Autoregressive models [J]. Multidimensional System and Signal Processing, 1999,10: 357-378
Prediction Research of Non-stationary Data Based on Time-Varying Autoregressive Model
Wang Lina, Jiang Xiangduo, Lu Yuhua
(Experimental Center of Shaanxi Fast Group Company Institute, Xi’an 710119, China)
As the AR(Autoregressive) model has poor prediction effect on non-stationary data, a Time-Varying Autoregressive model is established for timing prediction. Point and interval predictions of the TVAR Model are conducted based on NL data of an aero-engine, and are compared to point prediction of the AR model. The result shows that the TVAR model can reflect the real trend of the data, and the prediction errors are in the allowable range. At a given confidence level, the TVAR prediction interval contains real data, so the TVAR model has better prediction results in the timing projections.
Time Series; Time-Varying Autoregressive Model; Prediction
TP391
A
2014.05.27)
王莉娜(1983-),女,陕西法士特汽车传动研究院,工程师,硕士,研究方向:机械设备故障诊断分析,西安,710119
姜相夺(1983-),男,陕西法士特汽车传动研究院,工程师,学士,研究方向:机械设备故障诊断分析,西安,710119
芦玉华(1986-),男,西安华为技术有限公司,工程师,硕士,研究方向:云计算虚拟化容灾,西安,710075
1007-757X(2014)08-0034-03

