GA-SVM 模型在煤质分析中的应用

杜宁，黄喜军，肖洪

GA-SVM 模型在煤质分析中的应用

杜宁，黄喜军，肖洪

利用支持向量机建立工业分析与元素分析的转化模型, 并采用遗传算法对工况进行参数寻优（即GA-SVM模型），为燃烧提供了更好的指导。实验结果表明，模型具有更高的预测精度，且适用于更宽的煤质范围，研究成果具有一定理论意义和应用价值。

煤质；工业分析；元素分析；支持向量机（SVM）；遗传算法(GA)

0 引言

煤的元素分析为研究煤的燃烧提供基本数据，是指导燃煤锅炉合理燃烧的前提，但煤的元素分析实验项目多，时间长，操作复杂，对化验人员要求高，其开展收到极大限制，通常电站无力开展此项研究，而煤的工业分析实验较简单，电站可自行测定[1]。所以，如何建立煤的元素分析与工业分析之间的相互转化模型，就显得尤为重要。

目前，在利用工业分析预测元素分析方面，传统方法是采用回归分析方法将元素分析与工业分析相关联，但是，元素分析与工业分析存在着复杂的非线性关系。传统方法只是两者之间的多元线性相关，对于特定的煤种，单煤种效果较好，对于宽范围的煤种和混煤，只是粗略的估算。对于非线性方法应用，大都是采用神经网络建立元素分析与工业分析之间的非线性关系,支持向量机（SVM）是当前应用比较广泛的非线性预测建模工具，与人工神经网络方法相比，支持向量机模型的预测精度更高，速度更快[2]。本文提出利用基于遗传算法（GA）优化的支持向量机（SVM）方法来建立煤质工业分析与元素分析之间的预测模型。

1 支持向量机回归算法与遗传算法

1.1 支持向量机回归算法

支持向量机回归算法的基本思想是通过一个非线性映射将输入向量映射到高维特征空间，并在该空间进行线性回归[3]。ε-SVR是Napkin等人提出的一种最常用的支持向量机回归算法，由于引入ε-（不敏感损失函数）使SVM从分类领域推广到回归领域；通过引入惩罚系数C实现算法结构风险最小化原则；引入核函数可以解决由于维数变大带来的维数灾难，这样就可以把选择非线性映射转化成选择核函数，最后转化为求解凸二次优化问题，且能保证找到的极值解就是全局的最优解。

1.2 遗传算法

遗传算法是由美国Michigan大学Holland教授于1975年首先提出的[4]。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。主要步骤包括编码、种群初始化、选择、交叉和变异。其本质是一种高效、并行、全局搜索的方法，他能在搜索过程中自动获取和累积有关搜索空间的知识，并自适应地控制搜索过程以求得最优解。遗传算法的一个显著优势是不需要目标函数明确的数学方程和倒数表达式，同时，又是一种全局寻优算法，不像某些传统算法易于陷入局部最优解，寻优的效率高，速度快[5]。

1.3 基于GA的SVM参数优化法

1.3.1 核函数的选择

在支持向量机回归算法中，核函数的选择对回归分析有很大的影响，但是，目前对于如何选择核函数还没有成熟的理论指导，常用的核函数有：径向基核函数、多项式核函数、Sigmoid核函数、线性核函数等。文献[6]研究认为径向基核函数比线性核函数好，在选择了径向基核函数后就没必要再考虑线性核函数；文献[7]认为Sigmoid核函数精度没有径向基核函数高，而且，不是完全正定的，在满足一定条件后它才能成为有效的核函数，一般情况下Sigmoid核函数不比径向基核函数好；多项式核函数当其阶次较高时会导致数值计算困难，耗费大量资源和时间[8]。因此，本文在建模时选择径向基核函数

1.3.2 支持向量机三参数寻优

采用径向基核函数后，支持向量机模型中有3个重要参数，分别是核函数的参数σ，惩罚参数C，不敏感损失函数系数ε。核函数的参数σ影响样本数据在高维特征空间中分布的复杂程度；惩罚参数C越大，过拟合现象就越明显，C越小，欠拟合现象就越明显，参数C影响算法复杂度，避免过拟合；置信区间的宽度是由不敏感损失函数系数ε的大小来决定的，可以反映函数拟合的精度，起到调节模型复杂度和逼近精度作用。这3个参数将影响SVM模型的泛化能力和收敛速度。利用GA算法对支持向量机这3个参数进行寻优，适应度函数设置为目标输出值的5-fold交叉验证误差，寻优步骤如图1所示：

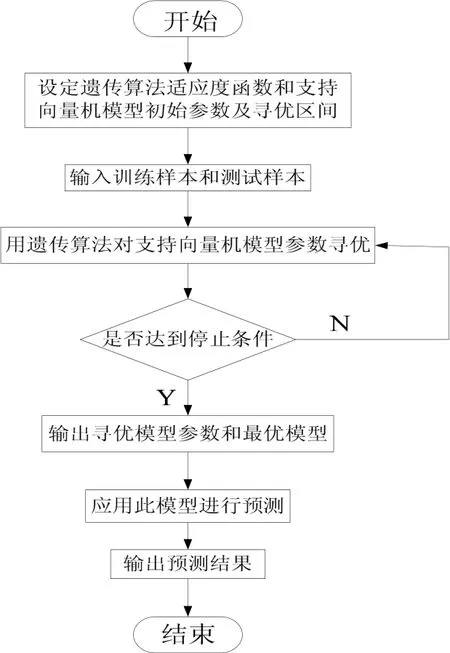
图1 支持向量机三参数寻优流程图

2 煤质分析的GA-SVM模型

2.1 煤质数据分析

文献[9]认为：门捷列夫经验公式利用煤的元素分析对其热值进行估算，同一种煤发热量用实验测量值和经验公式计算值之间的误差一般不超过3%～4%，所以，如果误差超过4%，就认为该煤质数据分析不可靠，予以剔除，最后，从186煤质数据中挑选出154个有效数据，这些媒质数据包括煤的工业分析、元素分析、干燥无灰基高位发热量、收到基的低位发热量和煤的种类。随机选择有效样本中的124个样本作为训练样本，剩下的30个样本作为测试样本，训练样本和测试样本都包括了较大范围的贫煤、烟煤和褐煤，煤的分类如表1所示：

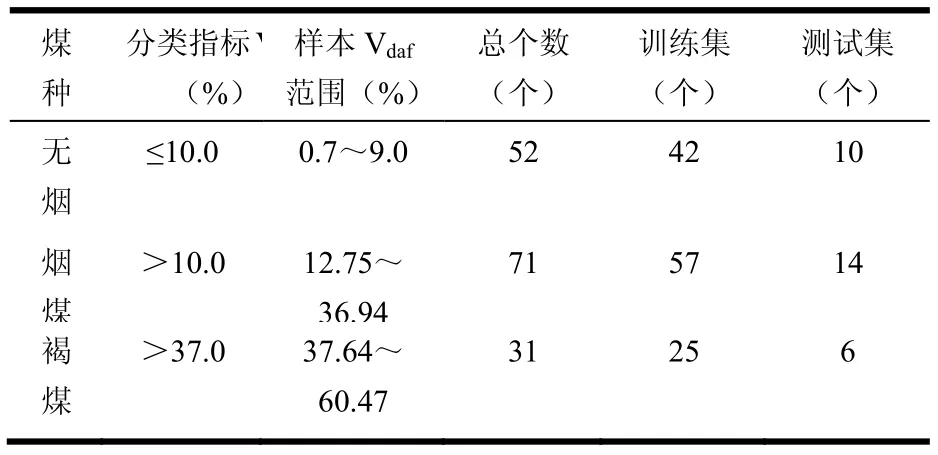
表1 煤样分类

在建模前要对数据样本进行[0～1]归一化处理，提高预测精度。

2.2 基于GA-SVM方法的预测建模

本文利用GA-SVM建立以下4种煤质工业分析与元素分析的转化模型：

（1）建立预测收到基Har元素的计算模型（输入为参数为煤质低位发热量Qar,net、收到基水分Mar、收到基碳含量Car、收到基氧含量Oar、收到基灰分含量Aar，输出为收到基氢含量Har）；

（2）建立预测挥发分干燥无灰基Vdaf的计算模型（输入参数为煤质低位发热量Qar,net、收到基水分Mar、收到基灰分含量Aar、收到基碳含量Car、收到基氢含量Har、收到基氧含量Oar、收到基氮含量Nar、收到基硫含量Sar，输出为挥发分Vdaf）；

（3）建立预测收到基碳元素Car的计算模型（输入参数为煤质低位发热量Qar,net、收到基固定碳含量FCar、收到基灰分含量Aar、收到基挥发分含量Var，输出参数为收到基碳元素含量Car）；

（4）建立预测干燥无灰基碳元素Cdaf的计算模型（干燥无灰基高位发热量Qar,gr、干燥无灰基固定碳含量FCdaf、干燥无灰基挥发分含量Vdaf、干燥无灰基氢元素含量Hdaf、干燥无灰基硫元素含量Sdaf，输出参数为干燥无灰基碳元素含量Cdaf）。

在建模过程中，设核函数的参数σ，惩罚参数C，不敏感损失函数系数ε寻优区间分别为（0～100）（0～100）（0～1）。遗传算法种群数目为20，交叉率为0.9，变异率0.01，最大迭代次数为200，适应度函数值为目标输出的5-fold交叉验证误差。在Matlab的环境下，4种模型的参数寻优结果如表2所示：

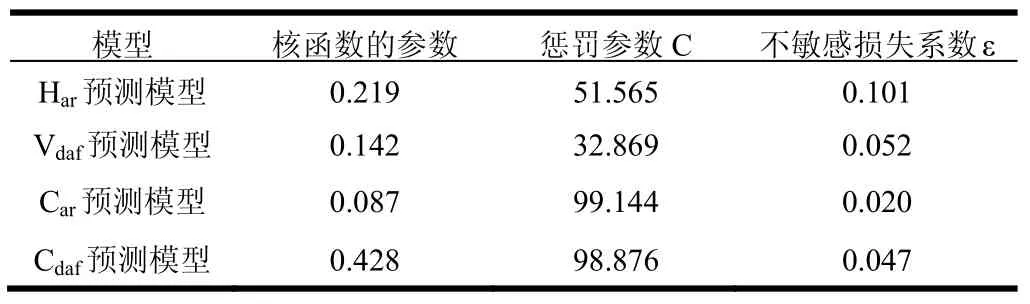
表2 四种模型的参数寻优结果

预测结果如图2所示：

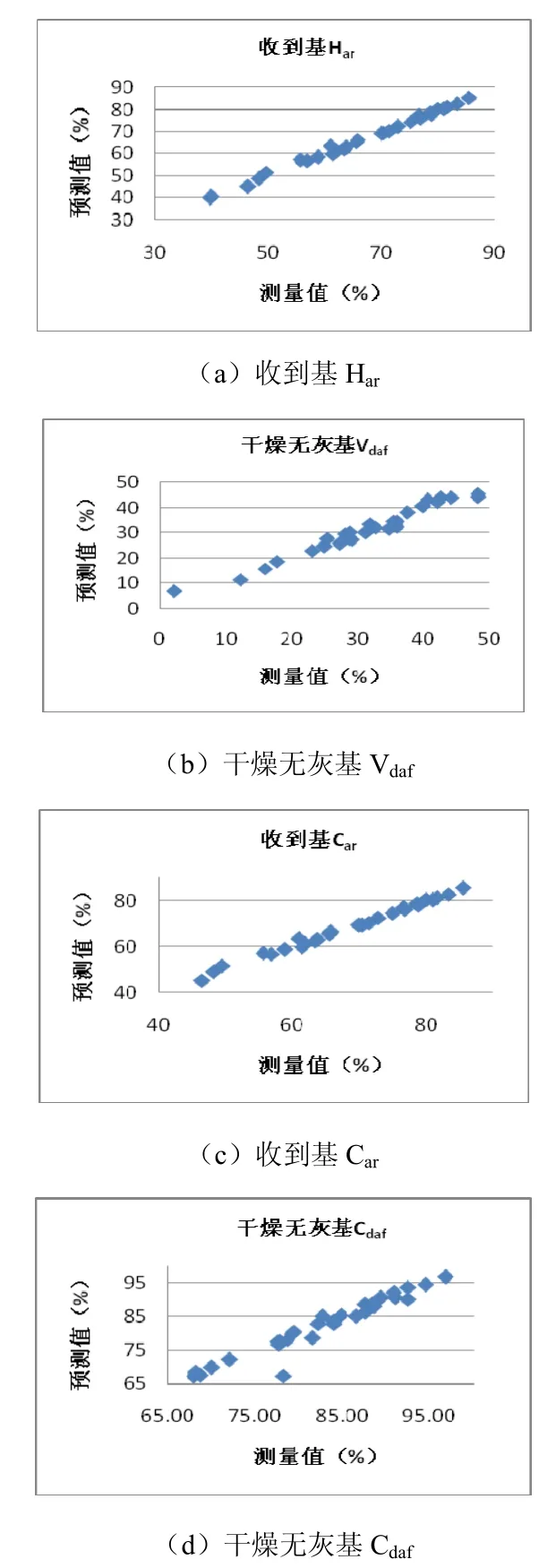
图2 四种模型的预测结果

2.3 误差分析

本文以均方根误差（RMSE）、平均相对误差（MRE）和线性相关系数r作为误差分析指标，将基于遗传算法的支持向量机模型（GA-SVM）与传统的基于网格搜索法的支持向量机模型(Grid-SVM)作对比，误差分析结果如下：

均方根误差（RMSE）是检验模型泛化能力的重要指标。均方根误差越小，模型的泛化能力越强，反之，模型的泛化能力就越弱。，GA-SVM模型的RMSE均小于Grid-SVM模型。所以GA-SVM模型的泛化能力强如表3所示：

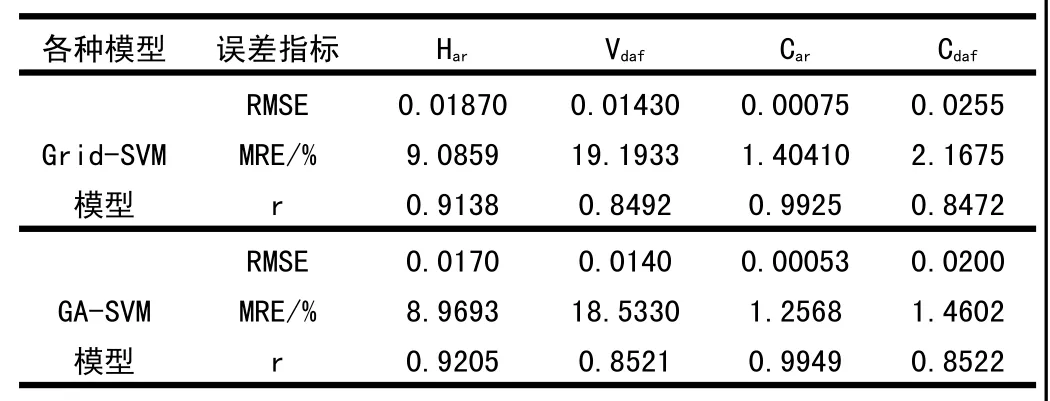
表3 两种模型的误差对比表

平均相对误差（MRE）是评价模型误差大小的重要指标之一，相对误差越大，说明模型整体误差比较大，预测精度不高；反之，预测精度就比较差。从表3可以看出，GA-SVM模型的MRE均小于Grid-SVM模型。所以GA-SVM模型的预测精度高。

线性相关系数r是用来衡量两个变量之间线性相关关系的指标,当0＜|r|＜1时，表示两变量存在一定程度的线性相关。表示两变量的线性相关越弱，一般可按3级划分：|r|＜0.4为低度线性相关；0.4≤|r|＜0.7为显著性相关；0.7≤|r|＜1为高度线性相关[10]。从表3可以看出，GA-SVM模型的线性相关性为显著相关，并且GA-SVM模型的线性相关性均强于Grid-SVM模型。

3 总结

从总体来看，线性相关系数越大，均方根误差与平均误差越小，说明模型的预测精度越高，从以上分析得出GA-SVM模型在预测精度上整体高于Grid-SVM模型。煤质包含了较大范围的贫煤、烟煤和褐煤，因此说GA-SVM模型还具有一定的通用性。

[1] 曹子栋.锅炉测试技术[M].西安：西安交通大学出版社，1995:1-20.

[2] 赵虹,沈利,杨建国,杨丽蓉,徐洪明. 利用煤的工业分析计算元素分析的DE-SVM模型[J]. 煤炭学报,2010,10:1721-1724.

[3] GB /T 476一2001,煤的元素分析方法[S].

[4] 赵义武，牛庆银，王宪成.遗传算法与蚁群算法的融合研究[J].科学技术与工程.2010.10（16）：4017-4020.

[5] Z.米凯利维茨.演化程序[M].周家驹，何险峰，译北京科学出版社，2000.

[6] keerthi K,Lin C J. Asymptotic behaviors of support vector machines with Gaussian kernel[J]·Neural Computation，2003，153(3):1GG7-1689.

[7] Lin H T, Lin C J. A study on sigmoid kernels for SVM and the training of non-PSD kernels by SMO-type methods[EB]. March 2003, http:/www.csie.ntu. edu. Tw/～cilin/papers.Html.

[8] 王春林,周昊,李国能,邱坤赞,岑可法. 基于支持向量机与遗传算法的灰熔点预测[J]. 中国电机工程学报,2007,08:11-15.

[9] 叶江明.电厂锅炉原理及设备[M].北京：中国电力出版社，2003:18-19.

[10] 王丽莉,李林侗,任雪等.基于房屋普查数据的房屋增长规律研究[J]. 防灾减灾报,2013,(3):9-12.DOI:10

The Research on the Application of Ga-Svm Model in Analysis of Coal Quality

Du Ning, Huang Xijun, Xiao Hong
(Institute of Mechanical and Electrical Engineering , Hohai University,Jiangsu Changzhou 213022)

Using genetic algorithm to search the optimum solution of the SVM model which was used to set up the transformation model (GA-SVM model) of industrial analysis and elemental analysis, so as to provide better guidance for combustion. The results show that, the model performs higher prediction accuracy and faster computing speed, and is suitable for a wider range of coal quality. Research results have certain theoretical significance and application value.

Coal Quality; Industrial Analysis; Elemental Analysis; Support Vector Machine; Genetic Algorithm

TP273

A

2014.07.10）

全国大学生创新训练计划（201310294041x）

杜 宁（1991-），男，陕西，河海大学机电工程学院，硕士，研究方向：热能与动力工程，常州，213022

黄喜军（1991-），男，广西，河海大学机电工程学院，本科，研究方向：热能与动力工程，常州，213022

肖 洪（1968-），女，常州，河海大学机电工程学院，副教授，硕士，研究方向：太阳能热发电、新能源与可再生能源的应用，常州，213022

1007-757X(2014)08-0049-03