一种基于序列计算的最近似K对数据搜索方案
刘义
一种基于序列计算的最近似K对数据搜索方案
刘义
多种应用场合需要寻找给定数据库中相似度最大的前k对数据。然而,由于应用领域需要处理的数据规模呈上升趋势,计算这样的最相似k对数据,难度非常大。提出了一种基于序列计算的最相似k对数据搜索方案,首先,将所有数据对分割成多个组,然后,提出了所有数据对分组算法和核心数据对分组算法,通过单独计算每个组中的最近似k对数据,从所有组的最近似k对数据中选择相似度最高的k对数据,进而正确地确定最近似k对数据。最后基于合成数据进行实验,性能评估结果验证了本文算法的有效性和可扩展性。
数据库;相似度;序列计算;数据搜索;分组
0 引言
在分子生物学、医疗成像和时序分析等诸多应用中,经常需要检测出哪些数据的相似度较高[1]。这些应用领域首先需要从原始对象中提取出多维向量(又称为特征),然后存储于数据库中以进行相似度检索。最近人们发现,可以基于单次相似度搜索来代替大量的相似度检索来处理多维数据库相似度搜索和数据挖掘算法。比如,采用分层聚类算法[2],在开始时将每个点都看成是一个聚类,然后基于距离函数(如欧几里德距离或曼哈顿距离)计算相似度,进而获得最相似的聚类,它们被不断合并,直到我们获得了所需数量的聚类。
基于相似度的方法的主要缺点在于,给定一个相似度函数后,相似数据搜索函数需要用户提供最小相似度阈值。然而,因为阈值与应用场合有关,所以许多应用情况下该阈值难以事先确定。更可行的方案是按相似度降序排列,计算最相似的k对数据。与传统的相似数据搜索方法相反,最相似k对数据搜索不需要我们提供最小相似度阈值。为此,本文研究了基于序列计算的最近似k对数据并行搜索方案。
1 相关工作
最近似数据对搜索问题是数据挖掘领域的研究热点问题之一,相继有众多的研究者对此问题展开了深入广泛的研究,例如,Corral等人[4]提出了空间数据库的最近似k对数据搜索算法,以克服考察所有数据对的盲目搜索算法带来的二次方复杂度。他们的算法针对空间和低维数据进行了专门改进,使用了R -树等高效的基于spatial disk索引技术; 设有n个d维数据,Pereira等人[5]提出了基于分治法的二维数据相似性查询算法,其计算复杂度为;Yang等人[6]提出了处理高维数据的相似性查询算法,其计算复杂度为;Salowe[7]和Lenhof[8]等人都分别提出了最近似k对数据搜寻算法,其中文献[7]得出的L∞距离的计算复杂度为;文献[9,10]提出了二维数据搜索算法。其中,文献[9]通过Voronoi图来反复降低搜索空间,而文献[10]使用R-树索引对树进行高效修剪。然而当增加数据维度d时,这些数据的计算复杂度均会呈指数上升。
另外,文献[11,12]分别提出了基于阈值的相似数据搜索算法,这些算法使用倒排索引进行数据修剪;为了利用Jaccard系数、余弦距离和重叠相似度等相似度指标进行最近似k对数据查询,文献[13]提出了一种基于反转列表的搜索算法。然而,这些算法都假设所有数据均可存储于主存储器中,对大型数据不具有可行性。为了实现相似数据并行搜索,Vernica等人[14]通过对文献[13]中的PPJoin+算法进行拓展,提出了基于MapReduce的新算法。然而,该算法只适用于集合数据,难以推广到本文多维数据最近似k对数据搜索问题。鉴于此,本文在现有工作的基础上,提出了一种基于序列计算的最近似K对数据搜索算法,并通过仿真实验验证了本文算法的有效性。
2 问题描述
3 基于序列计算的最相似k对数据搜索算法
对最相似k对数据搜索问题,盲目搜索算法TopK-B[14]计算每一对数据点的距离,计算复杂度为O( d⋅log k⋅ n2)。本节基于分而治之和分支-定界的思想,提出了两种新的数据搜索算法,下面将详细阐述。
3.1 TopK-D:分而治之算法
我们对文献[15]中只能搜索一组最近似数据对的分而治之算法进行改进,并将经过改进的最近似k对数据搜索算法称为TopK-D算法。
给定数据点D,我们利用超平面分割D中的数据点,重复搜索每边最近似k对数据。为了计算横跨超平面数据对的距离,文献[15]中的算法基于下一分割维度调用迭代过程,直到只剩下一个维度未被分割,此时当我们计算横跨超平面数据对的距离时对每个数据点只需考虑固定数量的距离计算任务即可。在计算d维数据最相似数据对时,文献[15]已经证明,当我们计算横跨超平面数据对的距离时,每一对数据的距离大于最近距离的数据点数量有O(4d)个。因此,当我们搜索最近似k对数据时,对每一数据点p,我们可以保证,有O( k+4d)个数据点距离p点距离小于等于第k对最相近数据对的距离。
TopK-D算法的伪代码如图1所示:

图1 TopK-D算法步骤
递归函数的输入为数据点分组时的维度m,k,(d−m+1)个数组Xm,...,Xd。所有数组Xi(m≤i≤d)包含相同的数据点,根据数据点的第i个坐标进行排序。首先,TopK-D算法检查边界条件是否小于等于2。如果条件满足,就返回该对数据。否则,算法将输入数据点分割成两部分,对每部分重复调用自身函数。在第6-9行,我们将每个数组Xi分割成大小相同的两个数组和且中的数据点在xm=l超平面的左边,在xm=l超平面的右边。
设H和δ分别是xm=l每一边重复调用函数所返回的数据对和H中第k组最相似数据对的距离。现在我们将要针对第m个坐标与l的距离小于δ的数据点重复调用自身,以计算横跨xm=l的数据对距离。设Bi(m≤i≤d)是第m个坐标在[l−δ,l+δ]范围内的数据点,且Bi按照第i个坐标升序排列。递归调用以m+1,k和Bi(m+1≤i≤d )为输入。当m+1=d时,我们沿着最后一个坐标的数组使用滑动窗口来计算距离。
时间复杂度:设每次递归时有n个数据点且分割维度为m,第6-9行分割(d−m+1)个数组Xm,...,Xd需要耗时O( d⋅ n),第28-30行选择范围在[l−δ,l+δ]内的数据点需要耗时O( d⋅ n)。因为每次递归调用两次递归函数时以n/2个数据点和第p个分割维度为输入,调用其他递归函数时以O( n)个数据点和p−1个分割维度为输入,递归操作耗时为T( n, p)=2T( n/2,p)+O( d⋅ n)+T( n, p −1)。在第1行,n=2时的边界条件是T(2,p)=Θ(1);在第15-27行,因为我们当m+1=d时有p=2,满足的边界条件是T( n,2)=O(logk⋅(k+4d)⋅n)。有了递归和边界条件,我们有T( n)=O(logk⋅(k+4d)⋅n(logn)d−1),该递归问题的解见文献[16]。
3.2 TopK-T: 分支-限界算法
本节我们将提出另一种最相似k对数据搜索算法TopK-T。在该算法中,我们不是存储LlS,而是利用空间为Θ(n)的最小堆QlS,以便我们可准确按照访问LlS的次序挨个访问下一最相似数据对。于是,我们只将每个数据点的下一最相似数据对存储到最小堆Ql中。当我们把点pi的最相似数据对从Ql中提取并删除时,我们将再次插入点pi的下一最相似数据对。
对每个维度l,我们首先按照D中数据点第l个坐标创建所有数据点升序列表Sl。设Sl[i ]是列表Sl第l个坐标的第i个点,Sl[i ](l)是Sl[i ]的第l个坐标。当我们刚开始创建最小堆Ql时,对每个点Sl[i ](1≤i≤n−1),我们把
堆使用的键。请注意,如果对Ll中的每一对数据pi,pj∈D施加条件i<j,则从第i个坐标距离角度来说,在Sl[i ]的所有不同数据对中,Sl[i+1]是数据点Sl[i ]的最相似近邻。
当我们每次迭代把最上面元素(dist, p, q)从最小堆Ql中删除时,被使用的数据对Sl[p]和Sl[q ]似乎是Ll中基于第l个坐标的下一最相似数据对。于是,考虑到Sl[q+1]是Sl[p ]出现在Sl[p ]之后的下一最相似数据点,Sl[p ]作为
TopK-T算法的伪代码如图2所示:

图2 TopK-T算法步骤
TopK-T算法开始时对空最大堆TOPk初始化,保存最相似的k对数据。对1≤l≤d的第l个坐标,我们首先根据l坐标对D中的每个数据创建有序数组Sl;对1≤i≤n−1的每个i,通过插入数组(Sl[i](l)−Sl[i+1](l),i, i +1)来创建最小堆Ql。While循环迭代一直持续到TOPk中有至少k对数据为止,且TOPk中第k对最相似数据的最大距离只能为未知数据对的距离下限T。当Ql没有更多元素时也可以停止循环。通过调用GetMaxDistance(TOPk),获得TOPk中第k对最相似数据的距离。每次While循环时,我们首先调用>PopMin( Ql),从Ql中提取出最上端的数组(Sl[p](l)−Sl[q](l),p, q )并将其从Ql中删除,用Sl[p](l)−Sl[q ](l)来更新ul,然后用ul更新T。此时,由于第l坐标与Sl[p ](l)最相似的下一数据点是Sl[q+1],只要q+1≤n条件满足,我们就将(Sl[p](l)−Sl[q+1](l),p, q +1)插入Ql。如果我们退出while循环,则TOPk中的数据对就可作为最相似k对数据如图3所示:
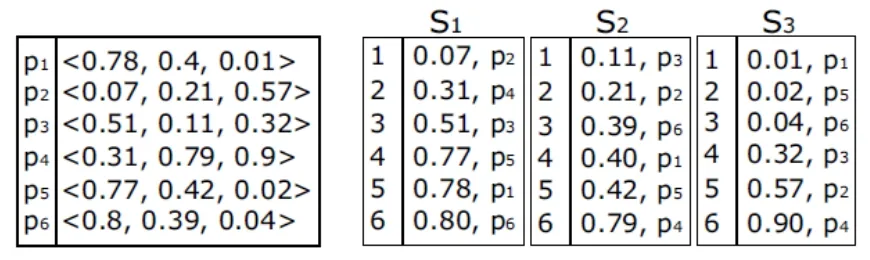
(a) D (b)有序数组图3 TopK-T算法的数据和有序数组示例
例如,考虑图3(a)中的数据集合D。假设我们想得出D中欧氏距离最相似的两对数据。我们首先生成列表S1, S2,S3,如图3(b)。初始时,对D中的每个数据p,Qi保存了点p与Si中下一个数据点的第i个坐标差值。于是,Q1为{(0.01,4,5),(0.02,5,6),(0.2,2,3),(0.24,1,2),(0.26,3,4)}。例如,Q1包含(0.01,4,5)是因为p5在S1中的数组下标是4,p5的下一数据点是p1,p1在S1中的数组下标是5。第一次访问Q1返回第一个坐标值之差为0.01的数据对(p5,p1)。(p5,p1)的距离计算后为0.02,我们将该对数据插入TOPk。因为p6在S1中排在p1之后,我们选择加入Q1的对象不是刚从Q1中提取出来的(p5,p1),而是数据对(p5,p6)的值(0.03,4,6)。首次访问Q1后,T为0.01。下次访问Q2返回数据对(p6,p1)的(0.01,3,4),距离为。数据对插入TOPk,且对数据对(p6,p5),(0.01,3,5)插入Q2,理由是p5在列表中位于p1之后。因为TOPk中有两对数据而且第2对数据的距离大于,我们继续执行while循环。对下次访问,我们返回Q1,用类似方法继续执行迭代步骤。在第7次访问时,我们从Q1中得到数据对(p,p),且。当前TOPk中的第2对最相近数据是距离为的数据对(p1, p6)。因为T大于TOPk中第2对最相近数据的距离,我们停止while循环。最后,两对最相似数据是(p1,p5)和(p1,p6)。
时间复杂度:每次迭代计算新数据对距离和更新Ql时,需要耗时O( d+logk+log n)。LlS的总大小为O( dn2),访问LlS的所有元素时TopK-T算法的时间复杂度为O( d2n2+dn2logk+dn2log n)。
综上所述,为了在每次分组时用化简函数找出最相似k对数据,我们可以使用TopK-B (盲目搜索),TopK-D (分而治之) 或TopK-T(分支-边界)算法中的任意一种。当我们在传统背景下只使用一台机器时,我们有两种选择,要么不进行分组,要么进行核心数据对分组。于是,我们有6种算法组合如见图4所示:

图4 不同算法示例
4 实验
4.1 实验设置
本节对本文算法进行性能评估。所有实验基于20个节点集群,配置Intel(R) Core(TM)2 Duo CPU 2.66GHz 2GB内存,Linux操作系统。所有算法用Java编译器1.6实现。所有实验使用欧氏距离作为距离度量。本节图形以对数标度来显示运行时间。实验数据采用合成数据,我们生成的合成数据在每一维上的数值均为实数且在0和1之间。为了生成逼真的合成数据集,我们让合成数据遵守Zipfian分布,如文献[17]所示,包含距离小于0.01的数据对的数据集群规模服从Zipfian分布,其中x是规模的秩,γ是确定数据点分布的参数。我们以γ=1.5默认值生成合成数据。此外,我们生成10和20维多种合成数据集,数据点数量从10,000 增加至10,000,000,生成数据的体积从95 MB 上升至3.8 GB。我们还将含有1,000,000个数据点的数据集的维度从2维增加至100维。
4.2 实验结果
TopK-B, TopK-D,TopK-T,TopKFB,TopK-FD和TopK-FT算法的性能,如图5所示:

图5 不同算法的实验结果对比
这些算法是没有运用MapReduce技术的主存储器算法。默认参数为:数据点数量n=50,000,维度数量d=10,拟搜索的最相似数据对数量k=50。对核心数据对分组,我们使用默认参数r=60,该值是每一维度区间的数量。
改变参数n:我们将参数n从5000增加至100,000,运行时间见图5(a)。当数据点规模范围在10000到20000之间时,TopK-T的性能最优。然而,当数据规模大于20000时,TopK-FT的性能最优,且速度是TopK-T的2倍。此外,当数据规模大于50000时,TopK-FB的性能优于TopK-T。因此,我们可以看出,本文核心数据对分组策略搜索到最相似k对数据的效率非常高。
改变参数d:下面实验中,我们将维数d从2维增加至100维。图5(b)给出了运行时间。d>10时算法TopK-D和TopK-FD的运行时间超过2小时,所以本文没有给出它们运行时间曲线。对于维度d为2-10维的数据集合,TopK-T的速度最快。然而,当d从10增加至100时,TopK-T的运行时间迅速上升。当50≤d时TopK-FB的速度是TopK-T的1.5倍。这一结果表明,低维数据最应选用TopK-T算法,且核心数据对分组对高维数据非常有效。
改变参数k:当k从2增加至100时,我们在图5(c)中绘出了算法的运行时间。当k变化较大时,TopK-FT的性能最优。在k的所有区间上,TopK-FT的速度大约是TopK-B的40倍,是TopK-D的5倍。因此,我们可以看出,核心数据对分组非常高效,且TopK-FT和TopK-FB基本不受参数k的影响。
5 总结
多种应用场合需要寻找给定数据库中相似度最大的前k对数据。然而,计算这样的最相似k对数据,难度非常大,因为应用领域需要处理的数据规模呈上升趋势。.本文研究了基于序列计算的最相似k对数据搜索问题,提出了一种新的算法用于最相似k对数据搜索,最后通过实验结果证明了本文方案的有效性和可拓展性。我们下一步工作的重点是将MapReduce技术用于大数据处理中,研究一种用于大数据分析服务的启发式云爆发算法。
[1] Böhm C, Braunmüller B, Krebs F, et al. Epsilon grid order: an algorithm for the similarity join on massive high-dimensional data[C]. ACM SIGMOD Record. ACM, 2001, 30(2): 379-388
[2] 李朝鹏,李肯立,成运,李朝建. 基于数据预处理的并行分层聚类算法[J]. 计算机应用研究, 2010,27(1): 71-73
[3] Lee K H, Lee Y J, Choi H, et al. Parallel data processing with MapReduce: a survey[J]. ACM SIGMOD Record, 2012, 40(4): 11-20
[4] Corral A, Manolopoulos Y, Theodoridis Y, et al. Algorithms for processing K-closest-pair queries in spatial databases [J]. Data & Knowledge Engineering, 2004, 49(1): 67-104
[5] Pereira J C, Lobo F G. An Optimized Divide-and-Conquer Algorithm for the Closest-Pair Problem in the Planar Case [J]. Journal of Computer Science and Technology, 2012, 27(4): 891-896
[6] Yang S W, Choi Y, Jung C K. A divide-and-conquer Delaunay triangulation algorithm with a vertex array and flip operations in two-dimensional space [J]. International Journal of Precision Engineering and Manufacturing, 2011, 12(3): 435-442
[7] Salowe J S. Enumerating interdistances in space [J]. International Journal of Computational Geometry & Applications, 1992, 2(01): 49-59
[8] Lenhof H P, Smid M. Sequential and parallel algorithms for the k closest pairs problem [J]. International Journal of Computational Geometry & Applications, 1995, 5(03): 273-288
[9] Katoh N, Iwano K. Finding k farthest pairs and k closest farthest bichromatic pairs for points in the plane[C]. Proceedings of the eighth annual symposium on Computational geometry. ACM, 1992: 320-329
[10] Qi S, Bouros P, Mamoulis N. Efficient Top-k Spatial Distance Joins [M]. Advances in Spatial and Temporal Databases. Springer Berlin Heidelberg, 2013: 1-18
[11] Chaudhuri S, Ganti V, Kaushik R. A primitive operator for similarity joins in data cleaning[C]. Data Engineering, 2006. ICDE'06. Proceedings of the 22nd International Conference on. IEEE, 2006: 5-10
[12] Sarawagi S, Kirpal A. Efficient set joins on similarity predicates[C]. Proceedings of the 2004 ACM SIGMOD international conference on Management of data. ACM, 2004: 743-754
[13] Xiao C, Wang W, Lin X, et al. Efficient similarity joins for near-duplicate detection[J]. ACM Transactions on Database Systems (TODS), 2011, 36(3): 15
[14] Vernica R, Carey M J, Li C. Efficient parallel set-similarity joins using MapReduce[C]. Proceedings of the 2010 ACM SIGMOD International Conference on Management of data. ACM, 2010: 495-506
[15] Bentley J L, Shamos M I. Divide-and-conquer in multidimensional space[C]. Proceedings of the eighth annual ACM symposium on Theory of computing. ACM, 1976: 220-230
[16] Monier L. Combinatorial solutions of multidimensional divide-and-conquer recurrences [J]. Journal of Algorithms, 1980, 1(1): 60-74
[17] Palmer C R, Faloutsos C. Density biased sampling: an improved method for data mining and clustering [M]. ACM, 2000
The Top-K Closest Pairs of Data Search Scheme Based on Serial Computation
Liu Yi
(Dalian Vocational & Technical College, Dalian116035, China)
There is a wide range of applications that require finding the top-k most similar pairs of records in a given database. However, computing such top-k similarity joins is a challenging problem today, as there is an increasing trend of applications that expect to deal with vast amounts of data. This paper proposes a top-k closest pairs data search scheme based on serial computation, firstly, the proposed scheme splits conceptually all pairs of points into partitions, and then the all pair partitioning and the essential pair partitioning methods are proposed, we can correctly find the top-k closest pairs by computing the top-k closest pairs in each partition separately and selecting the top-k closest pairs among the top-k closest pairs from all partitions. We finally perform the experiments with the synthetic datasets. Our performance study confirms the effectiveness and scalability of our algorithms.
Database; Similarity; Serial Computation; Data Search; Partitioning
TP391
A
2014.06.06)
刘义(1973-),男,汉族,辽宁建昌人,大连职业技术学院,硕士,讲师,主要研究方向:数据挖掘,网络安全,大连,116035
1007-757X(2014)08-0037-05

