基于自适应遗传算法的超声检测最优轨迹规划

张彦美，夏筱筠，柏 松

（1.中国科学院大学，北京100049；2.中国科学院沈阳计算技术研究所，辽宁 沈阳110168；3.中航工业沈阳黎明航空发动机 （集团）有限责任公司，辽宁 沈阳110043）

0 引 言

在超声波无损检测领域，轨迹规划对于提高超声检测效率具有重大的意义。因此近年来不少学者就此问题进行了研究，如Lin和陈勇旗等提出了遗传柔性多面体算法，以时间最短为目标寻找最优运动轨迹，但是该算法只是一种局部搜索算法；Tondu等人用光滑直线段连接各关键点，但这样产生的轨迹不能对给定点进行插值操作；王建滨等采用数值方法用动态规划技术对轨迹规划算法进行优化求解，但计算代价会随问题规模的增大而急剧增加。自适应遗传算法相对于以上方法具有鲁棒性好，适合解决一些复杂问题等的优点。因此，本文在考虑运动学等条件的约束下，运用自适应遗传算法进行时间最优运动轨迹规划。

1 运动学建模

1.1 坐标变换

相邻连杆坐标系如图1所示，用一组参变量来表示连杆和关节之间的关系：

（1）连杆杆长li：连杆Li两端关节Ai和Ai＋1中心连线的长度，即公垂线的长度。

（2）连杆扭角αi：垂直于li的平面内关节Ai和关节Ai＋1中心连线的夹角。

（3）连杆偏距di：连杆杆长li与li－1与关节Ai中心线交点之间的距离。

（4）关节角θi：垂直于Ai的中心线的平面内，li与li－1之间的夹角。

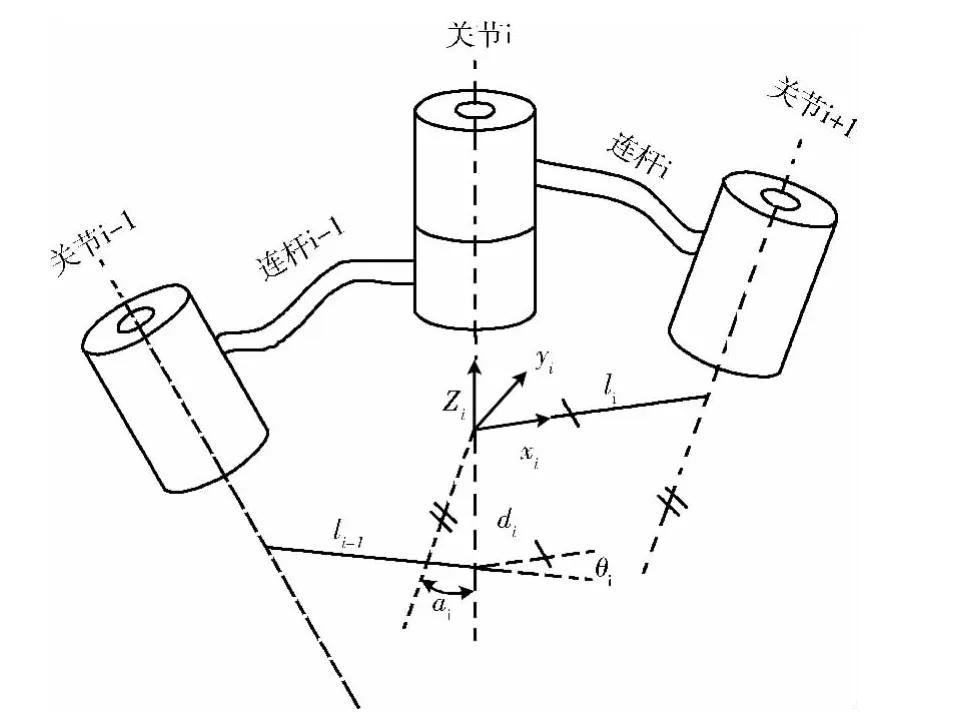
图1 相邻连杆坐标系

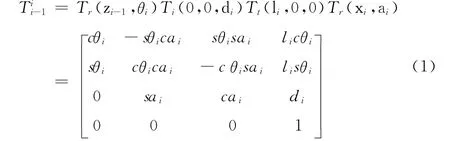
式中：s——sin函数，c——cos函数。由此可得，终端效应器相对于基础坐标系的坐标变换公式为

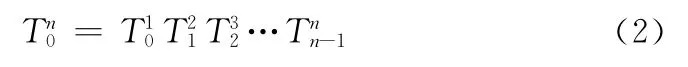
1.2 运动模型的建立

本文研究的是采用水浸反射法的超声检测系统，它的工作原理如图2所示。

它可以简化为有5个连杆（L1，L2，L3，L4，L5）、3个移动关节（A1，A2，A3）和两个转动关节（A4，A5）组成的系统。根据D－H法和连杆坐标系建立的原则建立如图3所示的各连杆坐标系，各连杆的结构参量、运动变量见表1，其中用x，y，z分别表示移动关节（A1，A2，A3）的变量值，用a，b表示转动关节（A4，A5）的变量值。

由式 （1）、式 （2）和表1得

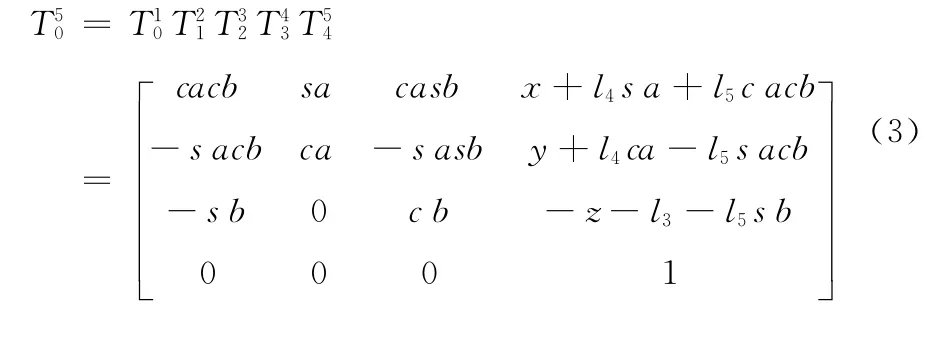
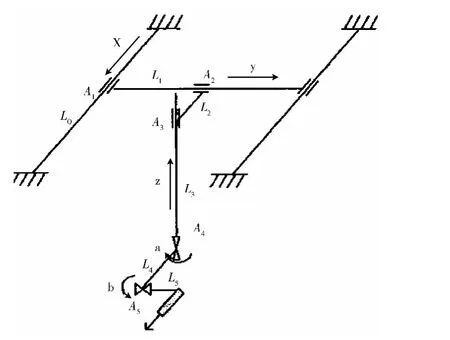
图2 运动原理

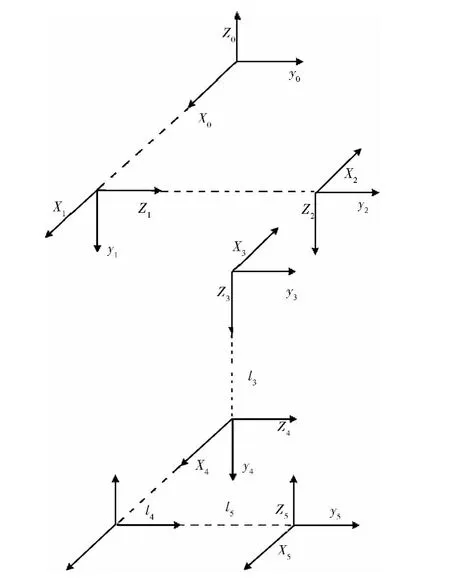
图3 连杆坐标系

表1 超声检测系统的连杆D－H参数

在几何空间中，用3个位置自由度和3个姿势自由度来表示超声探头在基础连杆坐标系中的位姿。用探头晶片的形心在基础连杆坐标系中的3个坐标分量来表示超声探头的位置自由度

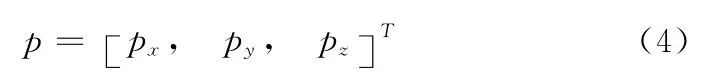
超声探头在基础连杆坐标系中的姿势坐标系可表示为

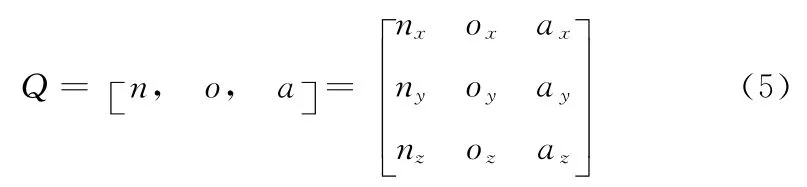
由式（3）～式（5）可得超声探头在基础连杆坐标系中的位姿可表示为

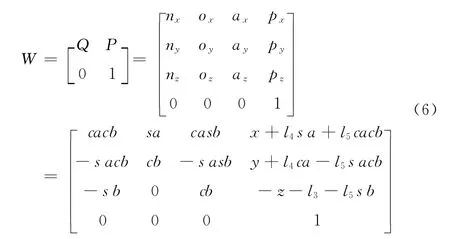
1.3 运动学方程的求解

在实际测量中需考虑水声距，设水声距为d，则根据式（6）及运动学方程正解可得点位值（即超声探头在空间某一点的位置和姿态）

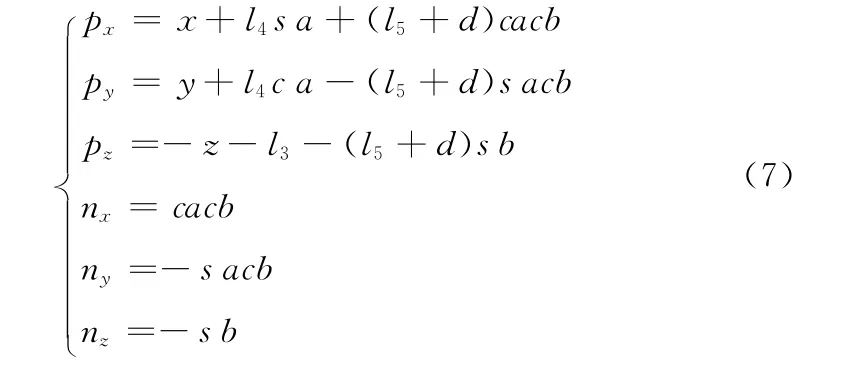
根据式（6）及运动学方程逆解可得运动点位值（即超声检测机械手各关节的变量值）

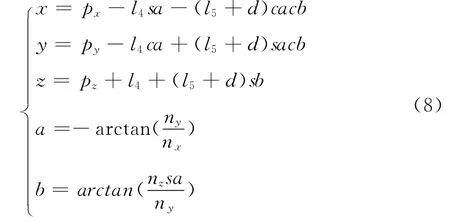
2 轨迹规划

2.1 目标函数

取一条扫描线上的采样点通过式（8）求得在关节空间的表示即关键点的坐标，然后对它们进行轨迹规划。设这些关键点表示为q1，q2，…，qn，对应的时间序列为t1，t2，…，tn，各个相邻关键点的时间间隔为h，则hi＝ti＋1－t［10］i原字符串。在超声检测时，各个关节同时从起始关键点开始运行，在ti时刻同时经过关键点qi，最后同时到达终点，即各个关节运行总时间是一样的且在相邻关键点之间的时间间隔也是相同的。因此我们设运行总时间为T，则T＝h1＋h2＋…＋hn－1。本文以最短时间为目标即求minT。

2.2 轨迹方程的确定

采用三次方程对轨迹进行拟合，设第i段的轨迹方程为

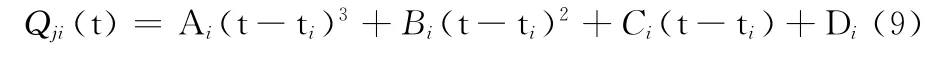
其中t［ti，ti＋1］，i＝1，2，…，n－1，j＝1，2，…，m。

则

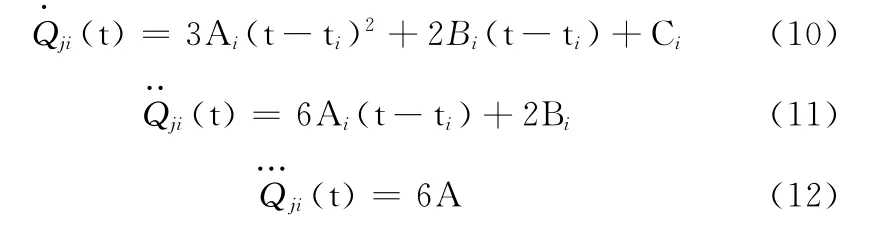
第j个关节在第i段的位移为Qji，，j＝1，2，…，m，i＝1，2，…，n－1，各关节在各采样点还满足以下条件：

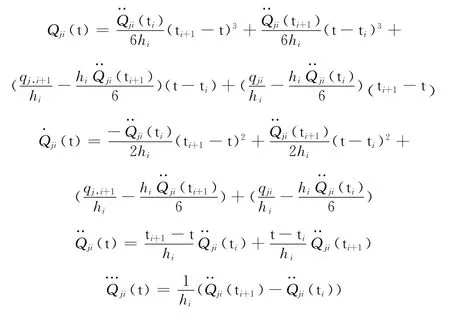
2.3 约束条件

所求的方程还必须满足实际要求的需要，如不能超过电机的额定速度、加速度等。设VMj，AMj，JMj分别为第j个关节允许的最大速度、加速度及跃度，j＝1，2，…，m。

3 轨迹规划遗传算法的设计

算法实现步骤：

（1）参数设置：设置种群规模N，迭代次数T，交叉概率pm及变异概率pc。

（2）产生初始种群：算法设计以运行时间最短为目标，遗传算法 的 个 体x就 设 为 ［h1，h2，…，hn－1］，其 中hi＞用实验的方法选取5s作为上界，然后在此区域内生成N个个体。

（3）计算适应度函数：本算法的目标函数为obj（x）＝且要求种群中的个体要满足2.3节中的条件，对于不满足条件的，采取惩罚措施，用自适应惩罚函数来处理，令惩罚函数：

其中

其中，j＝1，2，…，m。

适应度函数func＝1／（obj（x）＋p（x））。

（4）选择：采用轮盘赌方法，选择某操作的概率通过这个假设的适应度与当前群体中其他成员的适应度的比值而得到［12］。

（5）交叉与变异：采用单点交叉与基本位变异，在个体编码串中随机设置一个交叉点，在该点交换两个配对个体的部分基因并对个体编码串以变异概率p随机指定某一位进行变异操作［12］。

（6）重复执行（3）～（5）操作，直至迭代次数达到T。

算法改进：传统的遗传算法的交叉概率和变异概率是事先确定的，容易产生局部最优解。而自适应的遗传算法的交叉和变异概率能够随适应度而自动改变，在一定程度上避免算法的 “早熟”问题［15］，所以选用自适应遗传算法对原来算法进行改进。其中，交叉概率pc和变异概率pm的计算如下

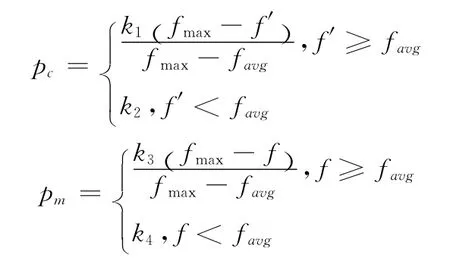
式中：fmax——每代种群最大适应度值，favg——每代种群平均适应度值。把这两个式子代入上面遗传算法的实现步骤中，即为自适应遗传算法的实现步骤。

4 算法实例

运动学约束见表2。

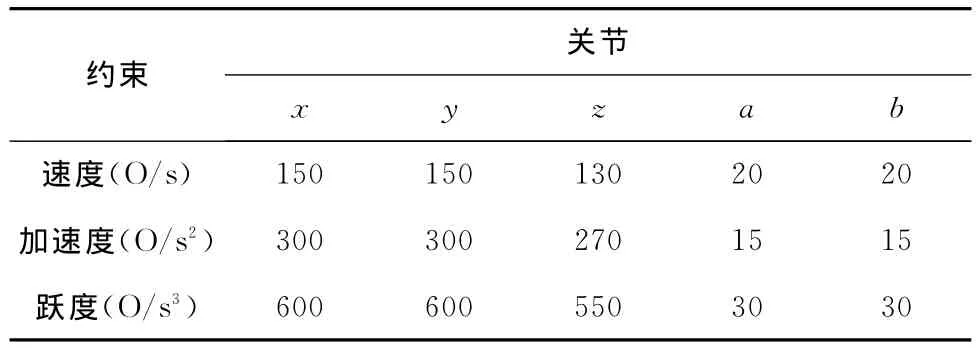
表2 运动学约束

其中，对于x，y，z关节O代表mm，对于a，b关节O代表dec。

选取关键点，利用式（8）转化为在关节空间中的坐标为：p1（300，250，100，－5，3），p2（200，210，200，10，－7），p3（240，120，290，0，10），p4（200，220，240，－10，－10），p5（270，130，200，3，0）。

设遗传算法的种群规模N＝80，迭代次数T＝100，交叉概率pc＝0.8，变异概率pm＝0.1，经过多次实验得到最优轨迹的时间节点向量为［1.45，1.2，1.35，2.04］，轨迹的最小执行时间minT＝6.04s。图4和图5分别为自适应遗传算法和基本遗传算法中运行时间随迭代次数变化的情况。

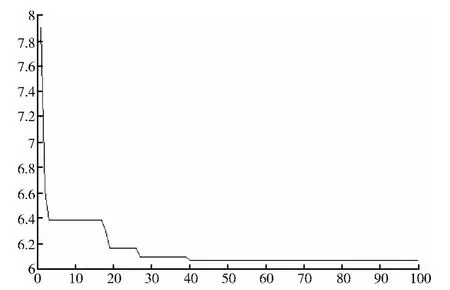
图4 自适应遗传算法时间优化曲线

图5 基本遗传算法时间优化曲线

由图4、图5可以看出，两种遗传算法中运行时间随迭代次数的增加而逐渐减小，最后趋于稳定，从而得到最优时间，但是自适应遗传算法能较快地得到最优解，并且能得到更小的运行时间，即用更小的时间就能得到最优解。其中，自适应遗传算法中各关节的位移、速度、加速度的轨迹曲线如图6～图8所示。

图6 各关节位置－时间曲线

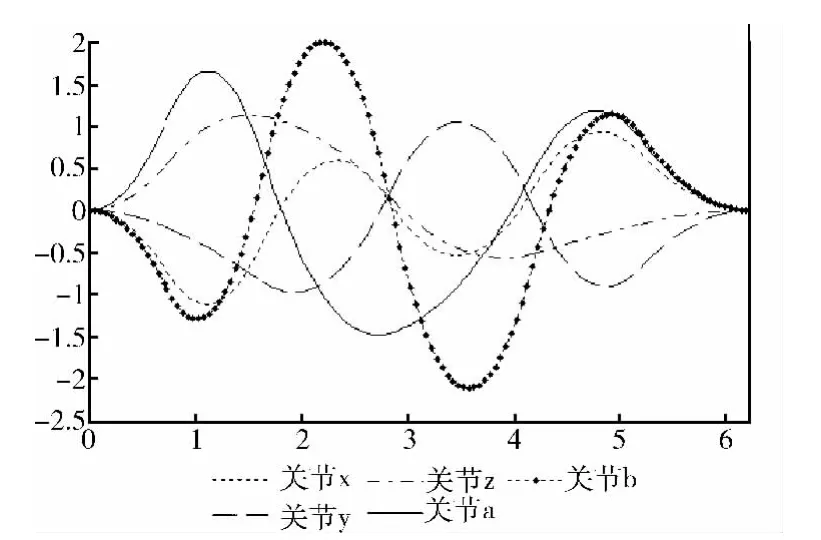
图7 各关节速度－时间曲线

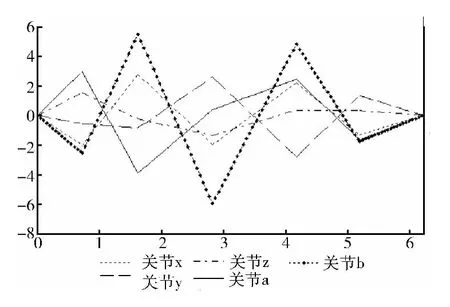
图8 各关节加速度－时间曲线

由图6～图8可以清楚看出各关节位移、速度、加速度随时间变化的情况，且各关节的速度、加速度均在规定的范围之内。

5 结束语

本文以时间最短为目标进行最优轨迹规划，采用三次样条函数对运动轨迹进行拟合，为满足各关节速度，加速度等的约束采用惩罚函数，利用自适应遗传算法得到了较好的效果。实验结果表明，该方法能够在满足各种条件的约束下对运行时间进行优化，并能够得到较理想的运动轨迹，说明此方法有效可行并能满足实际要求的需要，可在实际工程项目中推广应用。

［1］ZHENG Huifeng.Study on key problems of automated ultrasonic inspection for curved surface composite parts ［D］.Hangzhou：Zhejiang University，2008：19－33 （in Chinese）.［郑慧峰.曲面复合材料工件超声自动检测中若干关键问题的研究［D］.杭州：浙江大学，2008：19－33.］

［2］YU Yang，LIN Ming，LIN Yongcai.Optimal trajectory planning for industrial robot based on hybrid genetic algorithm ［J］.Computer Engineering and Design，2012，33 （4）：1574－1580（in Chinese）.［余阳，林明，林永才.基于混合遗传算法的工业机器人最优轨迹规划 ［J］.计算机工程与设计，2012，33（4）：1574－1580.］

［3］GAO Hao.Genetic algorithm with fitness estimation and its applications ［D］.Changchun：Jilin University，2011：6－17 （in Chinese）.［高浩.适应度估算遗传算法及其应用 ［D］.长春：吉林大学，2011：6－17.］

［4］DONG Jingyan，Ferreira P M，Stori J A.Feed－rate optimization with jerk constrains for generating minimum－time trajectories ［J］.International Journal of Machine Tools and Manufacture，2007，47 （12）：1941－1955.

［5］ZHENG Huifeng，ZHOU Xiaojun，ZHANG Yang.Time optimization based trajectory planning of ultrasonic inspection ［J］.Journal of Zhejiang University （Engineering Science），2010，44 （1）：29－33 （in Chinese）.［郑慧峰，周晓军，张扬.基于最优时间的超声检测轨迹规划 ［J］.浙江大学学报 （工学版），2010，44 （1）：29－33.］

［6］WU Siyuan，ZHOU Xiaojun，JIANG Jian，et al.Research of surface reconstruction and path generation by ultrasonic inspection ［J］.Journal of Zhejiang University （Engineering Science），2006，40 （5）：763－767.［吴思源，周晓军，江健，等.超声检测中曲面重构和路径规划方法研究 ［J］.浙江大学学报（工学版），2006，40 （5）：763－767.］

［7］LI Xiongbing.Study on key problems of automated ultrasonic inspection for complex surface parts ［D］.Hangzhou：Zhejiang University，2007：20－26 （in Chinese）.［李雄兵.曲面工件自动超声检测中若干关键问题的研究 ［D］.杭州：浙江大学，2007：20－26.］

［8］WU Siyuan.Study on key techniques of ultrasonic automated inspection for curved surface parts ［D］.Hangzhou：Zhejiang University，2006：17－26 （in Chinese）.［吴思源.曲面工件超声自动检测中若干关键技术研究 ［D］.杭州：浙江大学，2006：17－26.］

［9］ZHAO Zhenmin，LIU Feng，KONG Minxiu，et al.Industrial robot optimal trajectory planning algorithm ［J］.Journal of Heilongjiang Institute of Science ＆ Technology，2011，21（1）：69－73 （in Chinese）.［赵振民，刘锋，孔民秀，等.工业机器人最优轨迹规划算法 ［J］.黑龙江科技学院学报，2011，21 （1）：69－73.］

［10］WU Bin.The research on optimal planning of industrial trajectories ［D］.Lanzhou：Lanzhou University of Technology，2012：41－56 （in Chinese）.［吴斌.工业机器人最优轨迹规划研究 ［D］.兰州：兰州理工大学，2012：41－56.］

［11］LIU Ying.Research on fitness function in genetic algorithm［J］.Journal of Lanzhou Polytechnic College，2006，13 （3）：1－4（in Chinese）.［刘英.遗传算法中适应度函数的研究［J］.兰州工业高等专科学校学报，2006，13 （3）：1－4.］

［12］GE Jike，QIU Yuhu，WU Chunming，et al.Summary of genetic algorithms research ［J］.Application Research of Computers，2008，25 （10）：2911－2916 （in Chinese）.［葛继科，邱玉辉，吴春明，等.遗传算法研究综述 ［J］.计算机应用研究，2008，25 （10）：2911－2916.］

［13］ZHANG Xiaofei，ZHANG Huoming.Improved non－dominated sorting genetic algorithm II based on the elitist strategy［J］.Journal of China Jiliang University，2010，21 （1）：52－58（in Chinese）.［张晓菲，张火明.精英策略的改进非支配遗传算法 ［J］.中国计量学院学报，2010，21 （1）：52－58.］

［14］CHEN Guo，DENG Yan.Several new methods for features extraction based on genetic algorithm and their application［J］.Mechanical Science and Technology for Aerospace Engineering，2011，30 （1）：124－128 （in Chinese）.［陈果，邓堰.遗传算法特征选取中的几种适应度函数构造新方法及其应用 ［J］.机械科学与技术，2011，30 （1）：124－128.］

［15］CHEN Shizhe，LIU Guodong，PU Xin，et al.Adaptive genetic algorithm based on superiority inheritance ［J］.Journal of Harbin Institute of Technology，2007，39 （7）：1021－1024（in Chinese）.［陈世哲，刘国栋，浦欣，等.基于优势遗传的自适应遗传算法 ［J］.哈尔滨工业大学学报，2007，39（7）：1021－1024.］