面向大型数据集的聚类算法的优化与融合

于本成，鲍 宇，曹天杰，朱作付

（1.中国矿业大学 计算机学院，江苏 徐州221000；2.徐州工业职业技术学院 信息管理技术学院，江苏 徐州221000）

0 引 言

随着信息科技的发展，大规模、大容量的数据集开始出现并被广泛使用，其中包含了超多的文本、图像、视频和音频数据，而且需要从这些海量的数据中分析出需要的、有价值的数据，这就是数据挖掘技术的目标。聚类算法作为数据挖掘技术的具体实现方法之一，已经成为现今研究的热点方向。在大型数据集中使用传统聚类方式进行聚类主要面临两方面问题：第一，数据集高维比低维分布更稀疏，数据之间的距离几乎相等，一般的聚类方法都是基于距离进行聚类的，那么高维数据集则无法构建类［1］；第二，高维数据集中存的各类数据的属性基本无关，那么在所有维中存在类的概率基本为0［2］。然而对于任何的聚类算法都不可能适用于所有的数据集，因为有的要求运算效率高而对运算精度要求不高，有的是运算精度必须要高。针对上述问题本文提出部分优先算法，首先从原始集中分出第1类，在数据集中删除规划到第1类的数据，然后分出第2类，循环此操作，该算法效率高而运算精确度不理想，对于精度要求不高的数据集来说在运算效率上有较强的优势。

1 部分优先聚类算法 （partial priority algorithm，PPA）

1.1 概念定义

r－邻域：以某一数据点为圆心，以r为半径的区域。

典型样本p：若样本A里某数据的r－邻域内至少有Minpts（密度阀值）［2］个数据，则称为典型样本。

典型点C［3］：p中所有数据的均值为典型点

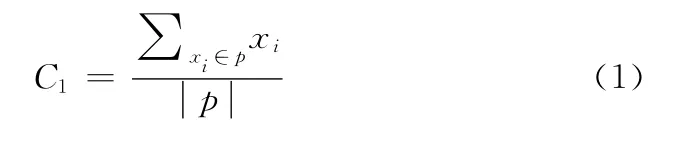
类中心［3］：类中所有数据的均值则为类中心。

1.2 部分优先算法的设计

在传统聚类算法的基础上，按照以下算法步骤设计部分优先聚类算法：

（1）在某一数据集中任意选取样本A，判断A的典型性。随机在A中取一点为初始点，并设定Minpts和r。设该点为中心，r－邻域内的数据数量大于Minpts，则A为典型样本；

（2）若A为典型样本，通过式 （1）求出样本中心既A的典型点C1；

（3）若A不为典型样本，则重复步骤 （1），至找到典型样本；

（4）找到典型样本后，以C1为中心进行聚类，通过

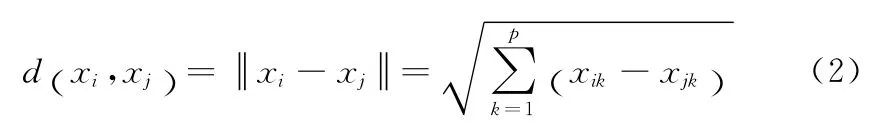
求出C1和A中每个对象间的距离；

（5）如果C1和某对象xi的间离小于r，则把该对象纳入A中，否则，计算C1与下个对象xi＋1的间距，直至遍历A中的所有对象。

该算法的流程如图1所示。

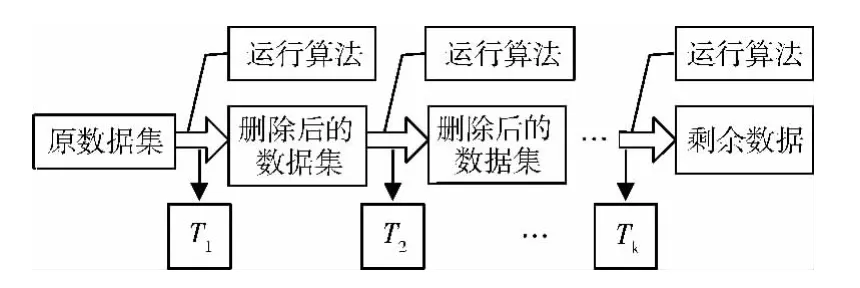
图1 部分优先聚类算法流程

1.3 PPA的优势

相比较于经典的聚类算法 （如K－mean聚类算法），此类算法包括一个具有n个数据的数据集，且因此产生的聚类数量为k，该算法的n个数据包含k个子集，表示一个聚类，相同聚类里的数据间距离很短，但是不同聚类里的数据间距离很大。用中心数值来代表每一个数据集，该中心值可由聚类里所有数据的平均数计算得到。

PPA为提高典型样本及典型点的选取效率，相对于传统聚类算法采用不选取完整数据集而通过随机样本的选取来寻找典型样本，且典型点的计算只有一次；同时PPA为提高典型点的典型性，提高r－邻域内数据密度，算法设计典型样本中的数据均值为典型点，该点亦可作为聚类的中心；以及PPA为降低原数据集的复杂度，算法设计在得到一个类后，同时将该类的数据从原数据集中剔除。

对于数据的顺序PPA是不敏感的，故PPA在球星数据和凸形数据方面的计算效果较好，而且PPA从样本均值处寻找典型样本，所以在处理异常数据方面就比较敏感，判断异常点精确。PPA在聚类过程中缩小了原始数据集，降低了原始数据集的复杂度，从而在效率方面更有非常明显的优势。PPA在算法效率方面、输入数据的敏感性方面、对异常数据的敏感性方面、发现聚类形状方面与K－means、DBSCAN、COBWEB、FCM、单连接、CLIQUE、CUBE等算进行比较［4，5］。结果分析见表1。

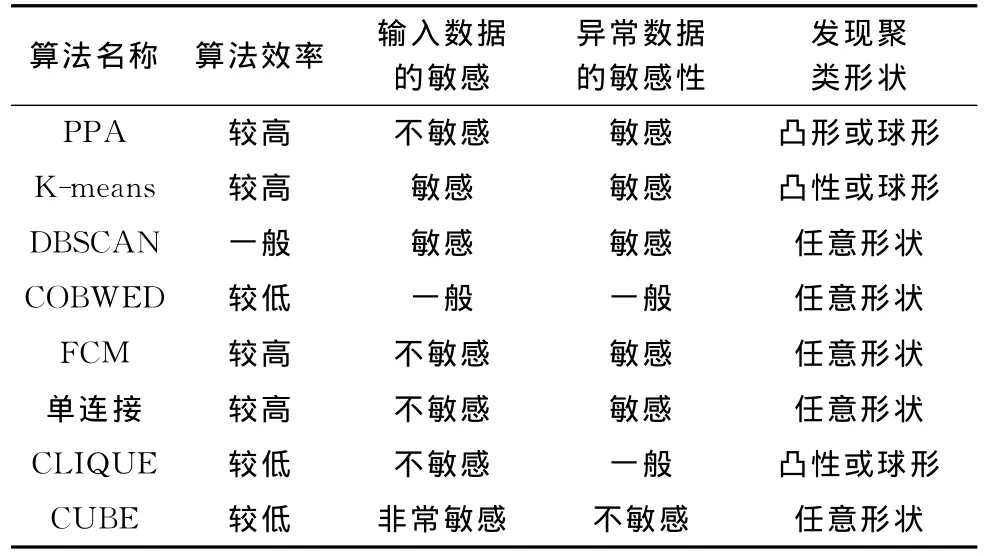
表1 算法的性能比较

2 面向大型数据集的PPA的聚类融合

部分优先聚类算法 （PPA）相对于传统的聚类算法在运算效率上有了明显优势，但在对于精度要求比较高的数据集计算上还有其固有的弊端。文章设计使用加权来确定类中心，提高类中心的典型性与稳定性，再通过聚类融合提高了算法的运算精度。最终算法在效果、可扩展性、稳定性、以及鲁棒性等方面均有显著提高。

2.1 聚类融合基本思想

聚类融合为克服单次聚类的不稳定性，将群体映射为数据点的相似度后进行融合而得到划分，对数据集的分类方式是选择使用一种算法下的不同参数或者多种算法。聚类成员的产生方法如图2所示。聚类融合的基本思想：设有n个数据点X＝，对X进行H次聚类得到H个聚类，π＝其中为第k次结果。设计共识函数г，如图3所示。

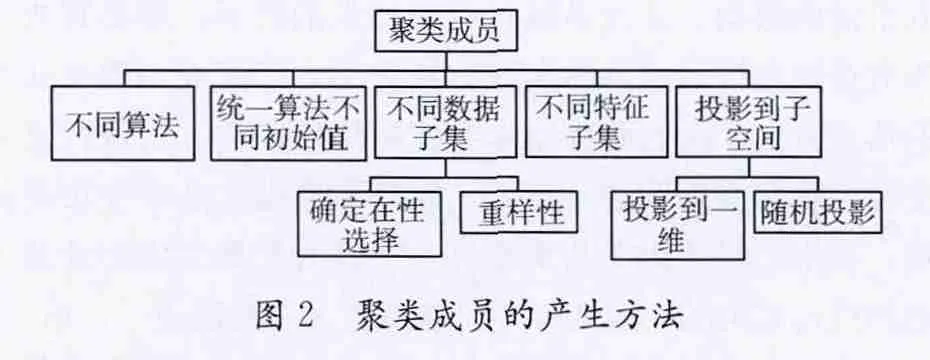
图2 聚类成员的产生方法

共识函数［6］的设计原则是只要能把需要聚类的各聚类成员以某种标准实现其融合，比如共协矩阵［7］（Co－association），其作用是衡量数据之间的相似度，计算公式为

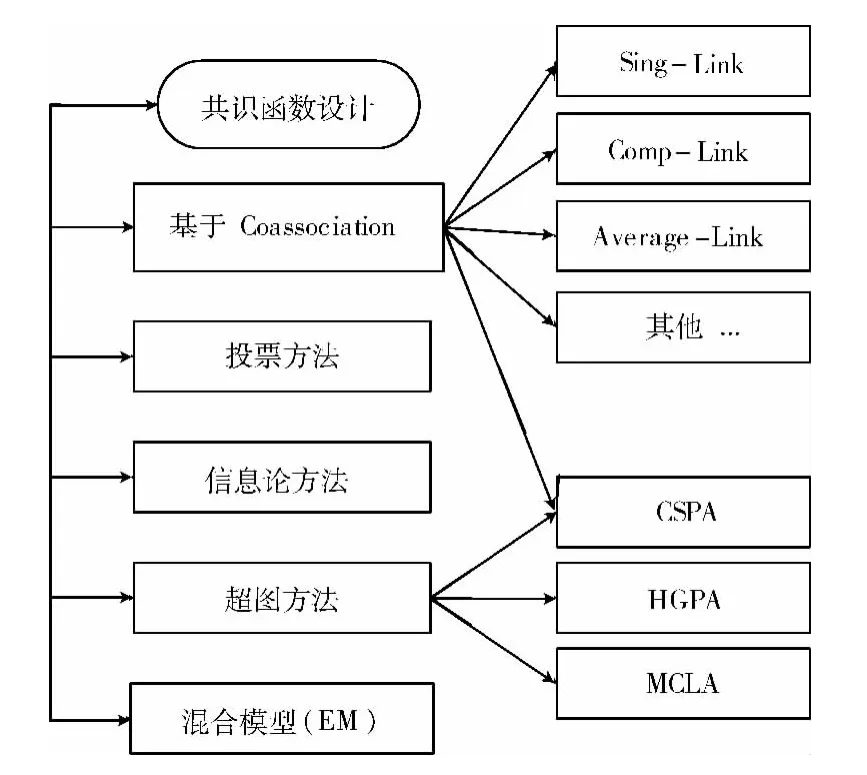
图3 设计共识函数

然后对H个结果进行融合后得到最终聚类结果π′。聚类融合的过程如图4所示。

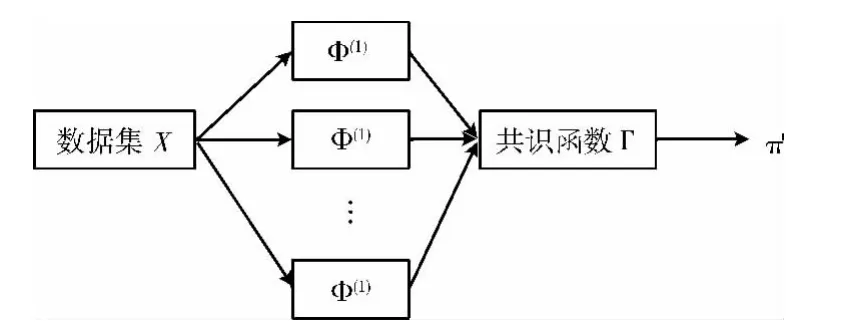
图4 聚类融合的过程

2.2 聚类融合算法的设计

融合方法的设计［8－10］是用加权的方式来计算第一类的类中心，该类中心的权重是通过该类内的所有数据量与每一类数据的总量之比来确定的

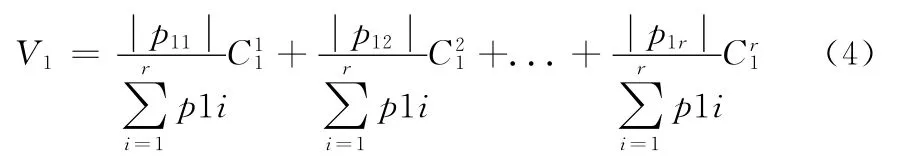
同样产生余下的k－1个类。由于的典型性，故产生T1，T2，...，Tk后，剩余在原数据集中的数据几乎为零，算法设计是把剩余数据均分为k份后按顺序分

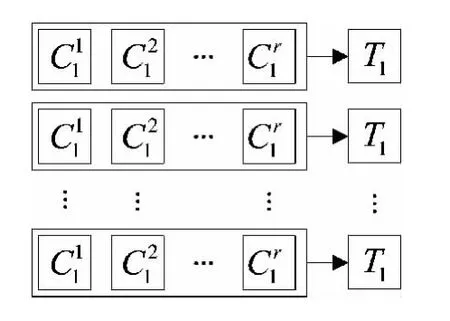
图5 各类的产生过程

2.3 聚类融合的优势

为使类中心的代表性和典型性更强以及分类精度更高，类中心采用加权的方式来确定，通过式 （5）来产生各个类中心。在提高算法效率方面，选取的类中心使得原数据集的数据尽最大减缩。在数据集复杂度方面，在分类的同时将已分类的数据从原数据集中删除，可以有效降低数据集的复杂度。

3 算法测试结果分析

本次试验选用9组来自 UCI Machine Learning Repository数据集 （Size＜2＊104），分别是Fertility，Car Evaluation，Abalon，Artificial Characters，ISOLET，CalIt2Building People Counts，Gas Sensor Array Drift Dataset，p53 Mutants，Letter Recognition见表2，测试算法可行性和稳定性，对表2所包含的9组数据集各运行5次K－means算法和PPA以及基于PPA的聚类融合算法，计算出平均时间和精度以及方差。

根据表3数据和图6曲线所示，在运算效率上，PPA算法相比较于基于PPA的聚类融合，PPA更有优势。但是随着数据集大小的增加，相比较于PPA算法，基于PPA的聚类融合算法在精度上的优势也随之变大，而这正是大数据集处理问题中，我们迫切需要解决的。

同时如表3和图6所示，根据实验数据结果中的方差比较，PPA有较好的鲁棒性。根据表4数据和图7曲线变化，可以判断基于PPA的聚类融合算法在应对大型数据集上抗干扰性和稳定性方面都有明显优势。由实验结果得出PPA算法和基于PPA的聚类融合算法受到数据量大小和维数的影响也较大，在数据为17000附近转折，前面较平稳，后面则时间增长太快。在精度方面在数据集大于6000时基于PPA的聚类融合算法开始平稳，可以推断的基于PPA的聚类融合算法稳定性高，对于未知数据集的计算有重要用途。

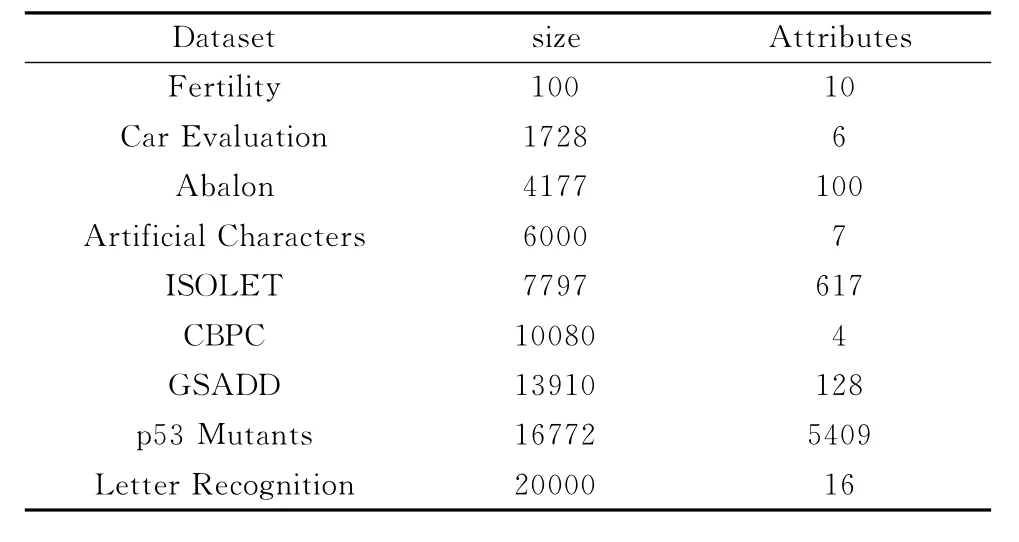
表2 实验的数据集

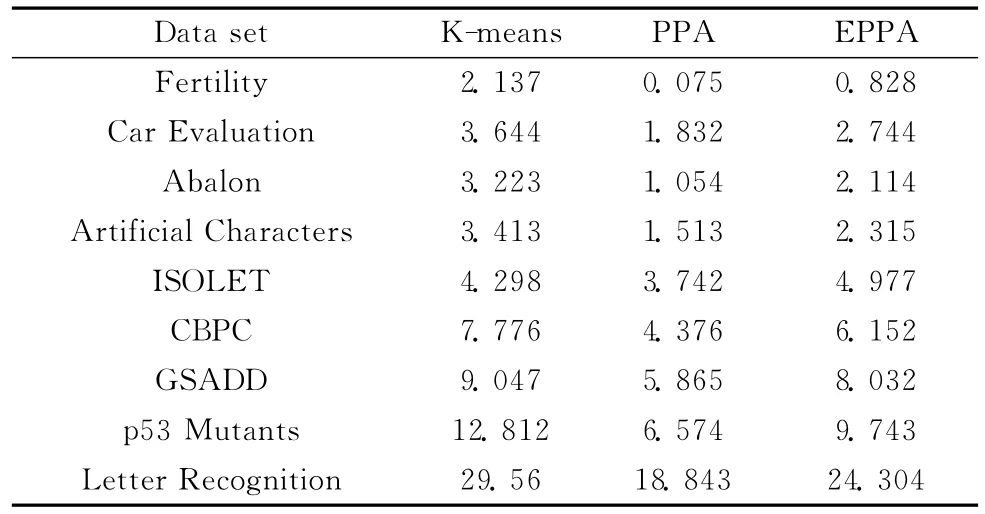
表3 算法运行时间 （sec）

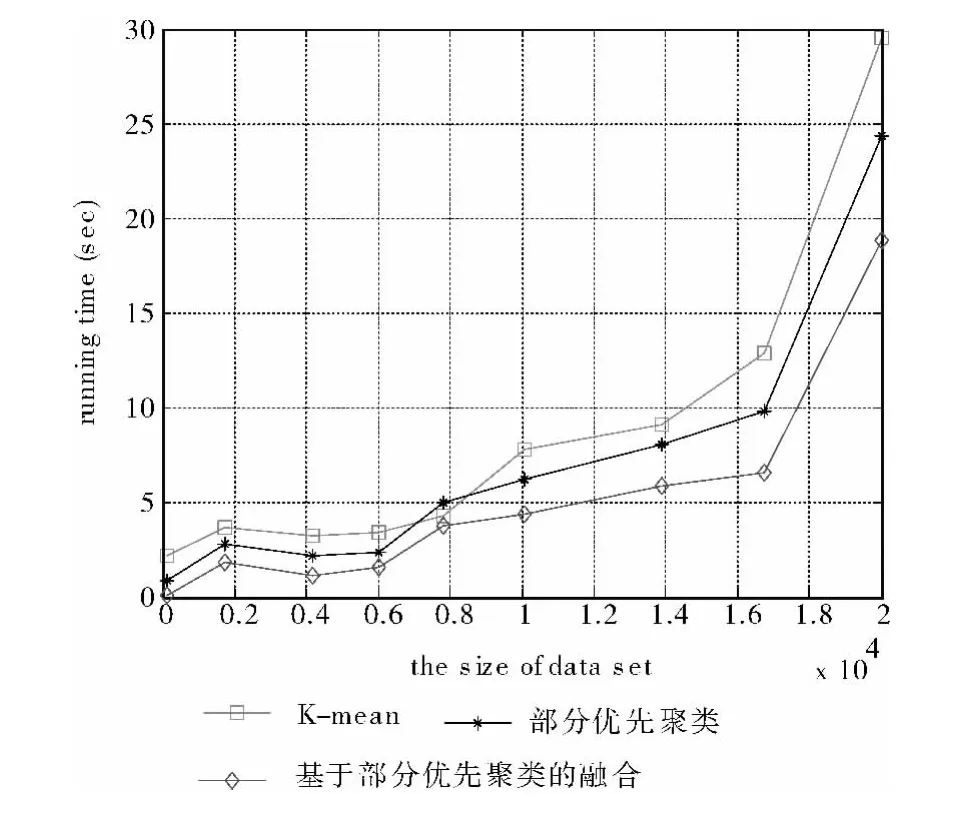
图6 运行时间比较

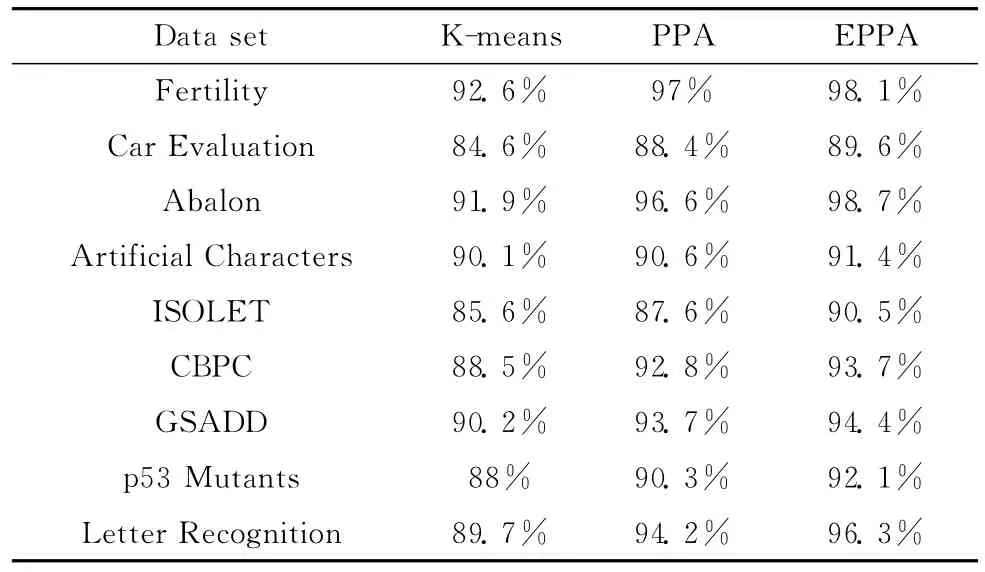
表4 算法精度

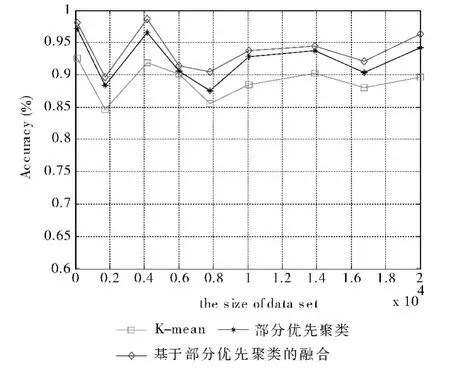
图7 精度比较

4 结束语

将传统聚类算法进行了优化，提出了部分优先聚类算法，相对于传统聚类算法 （以K－means为例），提高算法的效率，但在运算精度方面不为稳定。文章进一步在部分优先聚类算法的基础上进行了聚类融合，弥补了该算法运算精度不高的劣势，并通过实验比较了传统聚类算法，部分优先聚类算法和基于部分优先聚类算法的聚类融合在运算效率、运算精度方面的差异，得出了部分优先聚类算法和基于部分优先聚类算法的聚类融合分别适用于对运算效率要求高和对运算精度要求高的大型数据集上，并且在可扩展性、鲁棒性、稳定性等方面都有着传统聚类算法不可并论的优点，对于大型数据集的计算有着极其重要的作用。

［1］Chaitali Chaitali.Optimizing clustering technique based on partitioning DBSCAN and ant clustering algorithm ［J］.International Journal of Engineering and Advanced Technology，2012，2 （2）：212－215.

［2］Guyon，Lemaire P，Pinson E.Cut generation for an integrated employee timetabling and production scheduling problem ［J］.European Journal of Operational Research，2010，201 （2）：557－567.

［3］Shi TN，Wang JS，Wang PL，et al.Application of grid－based K－means clustering algorithm for optimal image processing ［J］.Computer Science and Information Systems，2012，9 （4）：1679－1696.

［4］Andreas Bley， Natashia Boland， Christopher Fricke.A strengthened formulation and cutting planes for the open pit mine production scheduling problem ［J］.Computers＆Operations Research，2010，37 （9）：1641－1647.

［5］Parvin H，Beigi A，Mozayani N.A clustering ensemble learning method based on the ant colony clustering algorithm ［J］.Appl Comput Math，2012，11 （2）：286－302.

［6］LIU Mingshu，FANG Hongbin，ZHANG Jian，et al.On effectiveness of attribute similarity in clustering algorithm ［J］.Computer Applications and Software，2012，29 （9）：146－147（in Chinese）.［刘明术，方宏彬，张建，等.属性相似度在聚类算法中的有效性研究 ［J］.计算机应用与软件，2012，29（9）：146－147.］

［7］Partha Sarathi Bishnu，Vandana Bhattacherjee.Software fault prediction using quad tree－based K－means clustering algorithm［J］.IEEE Transactions on Knowledge and Data Engineering，2012，24 （6）：1146－1150.

［8］ZHANG Hongwei，WANG Zhoujing.C－means clustering algorithm based on interval－valued intuitionistic fuzzy sets ［J］.Computer Applications and Software，2011，28 （2）：122－124（in Chinese）.［张宏威，王周敬.基于区间直觉模糊集的C均值聚 类 算 法 ［J］.计 算 机 应 用 与 软 件，2011，28 （2）：122－124.］

［9］Chattopadhyay S，Pratihar DK，De Sarkar SC.A comparative study of fuzzy c－means algorithm and entropy－based fuzzy clustering algorithms ［J］.Computing and Informatics，2011，30（4）：701－720.

［10］Shenbaga Ezhil S，Dr C Vijayalakshmi.An implementation of integer programming techniques in clustering algorithm ［J］.Indian Journal of Computer Science and Engineering，2012，3（1）：173－179.