基于FPGA的10G以太网并行CRC设计

袁 征，冶晓隆＋，郭 超

（1.国家数字交换系统工程技术研究中心，河南 郑州450002；2.69019部队）

0 引 言

循环冗余校验 （CRC）易于实现，且具有较优的误码检错能力和抗干扰性能被广泛应用于高速网络的差错控制中［1］。随着FPGA等可编程器件在骨干网络传输设备中的大量使用，基于异或逻辑的CRC校验在FPGA中易于实现、占用资源较少、且能实现线速网络数据的差错检测而成为骨干网络链路差错控制的主要方式［2］。

在IEEE802.3以太网协议中，CRC校验码是以太网帧结构中重要的组成部分。传统的CRC编译码器的实现都是基于串行方式，这种方式具有较高的工作频率和简单的电路结构，但是其采用串行移位，导致处理效率较低。随着网络速度的增长，尤其针对10G网络已经难以实现实时处理［3］。为此研究人员针对CRC校验的并行计算展开了研究［4－6］，文献 ［7］提出了基于流水线的并行CRC校验算法，该方法占用逻辑资源较少，但是处理单个周期需要8个周期的时延，无法满足实时处理要求。Stavinov［8］针对CRC校验的逻辑电路进行了改进，但是采用传统并行逻辑表，占用资源较多。文献 ［9］设计了一种多通道并行CRC，可以满足10G以太网的实时CRC校验，但算法设计复杂，对处理器性能要求较高。毕占坤［10］针对不同处理位宽分别设计了CRC校验模块，该方法处理性能较高，但推导复杂，难以实际部署应用。

基于此，本文提出了一种基于级联结构的CRC校验方法，通过此结构可以输出任意比特位的CRC校验值，解决了10G以太网非64比特结尾时需设计多种CRC逻辑而占用大量逻辑资源的问题，并改进了异或电路，降低了大量异或逻辑计算的处理时延。最后借助FPGA对本文方法进行了实现和验证。

1 CRC校验

1.1 CRC校验原理

CRC校验［11］利用线性编码理论，其基本思想是：发送方在发送k位信息序列时，以一定规则产生监督序列 （r位）并附在信息序列后面进行传送。接收方收到序列后，根据规则进行检验是否传输错误。

CRC校验码是一种采用多项式编码方式的循环码字。如图1所示，如果被检验序列有n位，则信息码为 ｛mn－1，mn－2，...，m1，m0｝，多项表达式 M（x）可表示为

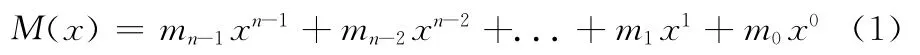
一般的CRC编码方式是：先将信息多项式左移r位，然后做模2除法。即

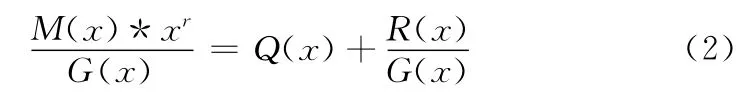
所得到的R（x）就是CRC校验码，其中G（x）为生成多项式。

图1 带CRC的数据序列

对于接收端，在收到信息序列M（x）后，如果其模二整除G（x）所得的余数等于接收的R（x），则没有误码。

G（x）的通用表达式为：G（x）＝xk＋gk－1xk－1＋gk－2xk－2＋...＋g2x2＋g1x＋1。以太网802.3协议对CRC校验的生成多项式进行了规定。

802.3 规定的CRC32表达式为：G（x）＝x32＋x26＋x23＋x22＋x16＋x12＋x11＋x10＋x8＋x7＋x5＋x4＋x2＋x＋1。

1.2 CRC编码过程

传统的CRC校验码可以通过线性移位寄存器 （多次迭代的移位异或运算）来实现。如图2所示，为通用的串行移位电路。其中：CRC校验码的余数用寄存器的状态 （存数）表示，模2除运算用异或表示。

图2 串行CRC编码实现原理

在图2中，r0、r1、…、rk－1为k个移位寄存器的存数，移位过程由外部时钟进行驱动，gi（i＝0、1、2、…、k－1）为生成多项式g（x）的系数，当gi为 “0”时表示断路，gi为 “1”时表示通路。串行电路作为基本的CRC运算电路，只需要移位寄存器和异或门来实现。

1.3 CRC并行算法

传统的串行CRC计算虽然实现简单，但是其每个周期只处理一位数据，对于具有n位的数据流来说，需要n个周期完成CRC值的计算，其对于高速网络通信数据的实时处理已经难以满足要求。并且基于硬件来实现多维数据（n维）的串行CRC计算时，需要使用n个存储器级的移位寄存器和2 n个异或门，占用了大量的运算资源，因此需要引入并行计算方法来提高处理效率。传统基于软件实现的并行CRC方法主要是查表法［12］，这种方法对于不同维数生成多项式序列和并行输入序列需要建立不同的余数表，占用了大量存储资源，并且查表深度和并行处理位宽呈2的幂次关系，不适用于硬件运算。因此提出了递推法和矩阵法［13］。

1.3.1 递推法

CRC并行算法是根据串行移位电路推导而来，如图2所示。对于串行移位计算，当前CRC的值只与输入信息序列的前一位和前一状态的CRC值有关。当进行并行计算时，以8位并行输入为例，8位信息序列同时输入与8位信息序列串行移位输入产生的CRC值相同，此时两种电路等效。由此可得出并行CRC计算的方法，即

以此类推，可以得到r81、…、r815。递推法计算并行CRC运算具有通用性，该方法消除了余数表，降低了对存储资源的需求，提高了计算速度，具有较好的扩展性。

1.3.2 矩阵法

递推法适用于并行输入维数较低的情况，当并行度较高时，递推运算较为复杂，因此提出了矩阵法计算。

以63位信息序列输入的CRC－32为例。如图2所示，记R＝ ［r0r1…r22r23］T为移位寄存器的当前状态，D ＝［d64d63…d1d0］T为第1至64个时钟的信息序列输入，R′＝［r′0r′1…r′22r′23］T为移位寄存器的下一个状态，R（64）为第64个时钟之后移位寄存器的状态。CRC－32并行设计就是找出函数关系R（64）＝f（R，D）。

由图2进行递推可得矩阵表达式

由式 （4）可得：R′＝T·R′＋S·d30＝T2·R＋TS·d31＋d·i30，以此类推，可得

其中所有代数运算和矩阵运算中的加法运算都为模2加。矩阵法将公式中的递推关系转化为矩阵运算，其更加直观，并且适用于大位宽数据的并行运算。但矩阵法涉及大规模的矩阵乘法运算，在硬件实现时需占用大量的存储资源和计算单元。因此，如何提高大位宽数据的并行CRC算法的计算效率和降低资源使用率成为一个重要的研究方面。

2 10G以太网中CRC设计

随着10G以太网技术大量应用于骨干网络链路和支持10G链路速率的MAC、PHY芯片的大量应用，使得基于高性能可编程器件FPGA结合以太网处理芯片 （MAC、PHY等）成为10G以太网处理设备的主流解决方案。

CRC校验作为网络数据处理流程的重要组成部分，随着网络速率的不断增长，为了满足线速CRC校验，基于FPGA等硬件实现的CRC计算成为主要方式。传统的并行CRC计算需要占用大量的存储资源和逻辑资源，降低了系统的处理性能。因此，研究新型CRC计算方法以降低系统功耗和芯片工艺的要求成为必要。

2.1 以太网中CRC校验

以太网通信中CRC校验具有重要作用，通信双方以约定的校验生成多项式和校验位宽实现数据传输的错误校验。包括对接收的数据帧进行CRC计算、当CRC错误时进行数据重传、发送数据帧时添加CRC校验序列和为下一跳节点提供数据检错依据等。通过CRC校验确保了以太网数据在整个链路中数据传输的可靠性。以太网数据传输中每个节点的CRC处理流程如图3所示，具体包括：

（1）数据收到物理层之后送到介质访问控制层（MAC）进行编解码处理，MAC层中首先进行CRC校验，通过比较计算的接收数据CRC值和接收的CRC值，当校验不一致时产生重传。

（2）对于CRC校验正确的数据帧，上传到上层进行处理，包括路由查表、TTL更新等。

（3）对于需要发送到下一跳 （next hop）时，首先计算待发送数据的CRC值，添加到数据序列组帧，为下一节点数据校验提供依据，最后送到物理层进行传输。

图3 以太网CRC校验和计算流程

以太网CRC校验遵循以太网IEEE802.3协议，IEEE802.3协议规定的以太网MAC子层的帧格式如图4所示，包括：源＼目的地址、长度、数据域和帧校验序列（frame check sequence，FCS），FCS校验的区域包括帧的协议字段和数据字段区域。

图4 以太网帧格式

在以太网通信中，以太网的字节序是大端模式 （高位在先），在计算FCS时首先需对帧内数据进行处理。IEEE802.3规定的以太网CRC校验计算步骤如下：

步骤1 对收到的帧进行字节内部高低比特翻转；

步骤2 寄存器初始值置为全1；

步骤3 利用并行CRC算法逻辑表计算CRC；

步骤4 对求得的CRC取反；

步骤5 取反后的CRC按照字节内高低比特翻转，得到以太网FCS。

2.2 基于级联结构的并行CRC设计

10G以太网接入系统中常采用64位并行数据通路，而FCS校验数据长度为60－1514字节 （如图4所示），使得以太网帧不一定结束在64比特边界，因此常转化为如图5所示的数据格式待处理。

图5 10G以太网64位并行数据接口

如图5所示，为10G以太网64位并行数据处理接口，其中Valid为数据有效指示，Sop为帧头部指示，Eop为帧结束指示，Data为以太网数据，每个周期为64比特，Size代表当前周期数据的有效比特数。

在传统并行CRC设计中，通常把数据处理分为两部分，对于Eop之前使用64位并行CRC32校验算法，对于Eop处则根据Size的指示位表示的数据有效位数选择8，16，24，32，40，48，56和64位CRC32校验模块中的一种来计算最后的CRC校验值，导致设计中必须设计以上所有位数的CRC校验模块，占用了大量的计算资源。

由式 （2）可得如下推论：

推论：已知序列X的CRC32为X’［31：0］，序列Y的CRC32为Y’［31：0］，设序列X’［31：24］的CRC32为Z［31：0］，则序列X的延拓序列 ｛X，Y｝的CRC32为

在已知8位的并行CRC32校验情况下，可以根据式（6）得到任意N位序列并行CRC32校验的表达式，并设计8－64位任意输入时并行CRC32表达式，如图6所示。其中间节点为

图6 基于级联结构的CRC编码器

如图6所示，为本文设计的基于级联结构的CRC编码器，其中CRC8模块为8位输入的CRC32校验模块，其根据式 （3）推导可得，CRC＿EXPAND模块为根据式 （6）设计的N位CRC－32校验模块，其中N＝8＊k，k＝1，2...8。采用以上级联模块可以输出任意N位的CRC校验值，通过SIZE和选择器MUX对Eop时任意字节的CRC32输出，从而避免了分别对需要对8，16，24，32，40，48，56和64位数据输入时的CRC校验模块设计，降低了存储空间。

CRC校验基于FPGA设计时的运算是对输入数据按比特的异或运算，如式 （3）所示，基于64位输入的CRC32运算需要多次异或运算，如d23甚至需要进行40多次运算，大量的组合逻辑产生的门延迟超出了系统的时延限度，尤其对于单个时钟周期的64位输入无法满足实时CRC处理要求。

异或运算取决于组合电路的具体结构。如组合逻辑A＝A1⊕A2⊕A3⊕A4⊕A5⊕A6的综合电路如图7所示，大量的异或次数导致了较大的时延。

图7 传统异或电路结构及时延

通过将传统的组合逻辑改为A＝（A1⊕A2）⊕（A3⊕A4）⊕（A5⊕A6），此逻辑的电路功能并未改变，其综合电路结构如图8所示。

图8 优化后的异或电路结构及时延

优化后的电路利用并行设计，将串行电路中累加的延时分散到了多个并行分支中，将门时延从5级降低到了3级。对于N位数据的异或操作，传统的按位异或将产生N－1级门延时，而图8的结构只产生 log2N （ 表示向上取整）级门延时，从而降低了异或操作的延时。对于多维数据的异或操作，此结构具有更大的优势，将使得延时以指数级减少，提高了处理效率。

3 实验验证及分析

3.1 实验环境及工具

为了验证本文方法的有效性和可靠性，搭建了实验平台进行验证。实验平台如图9所示。其中网络测试仪为Spirent公司的SMB600B网络测试仪，其具有1个10G网络端口。10G以太网处理板卡包括10G光模块和FPGA，FPGA型号为Xilinx公司的XC5VLX30，其中MAC帧处理通过FPGA中例化MAC核来实现。对网络测试仪发送的10G以太网数据在FPGA中计算CRC校验值并重新添加FCS域，打环返回到测试仪，利用测试仪集成的FCS校验功能判断所设计模块的正确性。

图9 并行CRC32验证平台

实验工具为普通PC机，该主机配备操作系统为Windows XP Professional SP3， 具 体 配 置 为：CPU 为 Intel Core2 1.86GHz，内存为2GB。实验仿真软件工具采用Xi－linx公司FPGA开发环境ISE13.3和以太网分析工具Wireshark。

3.2 CRC校验验证

为了验证基于FPGA的并行CRC校验算法的正确性，从网络获取实际以太网数据包，通过Wireshark可以看到该数据是完整的以太网帧，在每帧的结束位置包括一个帧校验序列FCS。本文获取了10G以太网中常用的校验方式CRC32以太网帧数据进行验证，结果如图10和图11所示。

图10 CRC32以太网数据包

图11 并行CRC32运算的VHDL仿真结果

如图10所示，为CRC32以太网数据帧，数据域的最后4个字节为FCS，其值为A6FF4847。将此以太网帧输入到本文所设计方法的仿真结果如图11所示，其中仿真时钟为200MHz，计算所得的CRC值为A6FF4847，与实际抓包值一致，说明了本方法的有效性。同时，基于64比特输入时，时钟采用200MHz，理论的速率为200x64＝12.8Gbps＞10Gbps，在帧结束的下一时钟周期即可计算出CRC值，说明本文所述方法满足10G速率的CRC实时计算。

3.3 资源利用情况及性能分析

对本文设计的并行CRC－32编码器进行综合布局布线，为了比较本文所述方法，并和传统的矩阵法和代入法所得的CRC32编码器进行比较，分别对以上两种方法的CRC32编码器同时进行布局布线，综合结果见表1。

表1 CRC32编码器综合布线结果

从表1可以看出，相比较代入法和矩阵法，本文所述方法在资源占用方面和传统方法近似，但输入输出延迟为3.7ns，处理效率提高了10%。允许的最高时钟频率超过250MHz，，完全可以满足10G以太网CRC校验的实时处理要求。

为了进一步验证所设计模块的有效性，通过打环测试（测试仪输出流量到FPGA进行FCS重计算，并将FCS添加到数据帧返回测试仪）进行分析。测试仪显示的相关结果见表2。

表2 10G网络测试仪的CRC32测试结果

从表2可以看出，在10G测试仪100%输出速率时，在78－1518字节的各种测试条件下，经过本模块计算的以太网数据帧FCS校验错误为0，丢包率为0，满足系统要求。

4 结束语

10G以太网CRC校验需要CRC算法满足实时性要求，本文提出了一种基于级联结构的并行CRC校验算法，并对算法中的组合逻辑电路进行改进。根据实际10G以太网中非64字节临界处理，通过传统8位CRC32校验电路产生级联的任意输入的CRC32校验电路，无需产生8－64位输入的所有校验电路，提高了处理的灵活性和降低了芯片使用面积。通过实际以太网数据包和网络测试仪进行实验验证，实验结果表明该方法具有较低的处理时延，可满足10G以太网CRC校验的实时处理要求。

［1］WANG Xinmei，XIAO Guozhen.Error correcting code：Principle and method ［M］.Xi’an：Xidian University Publisher，1991（in Chinese）.［王新梅，肖国镇.纠错码：原理与方法［M］.西安：西安电子科技大学出版社，1991.］

［2］LIU Lu，WU Mingliang，HE Junqiang.Implementation of error control based on cyclic redundancy check ［J］.Journal of Chengdu University （Natural Science Edition），2011，30 （1）：82－85（in Chinese）.［刘璐，武明亮，何俊强.基于循环冗余校验码的差错控制分析与实现 ［J］.成都大学学报 （自然科学版），2011，30 （1）：82－85.］

［3］ZHANG Youliang，LIU Zhijun，MA Chenghai，et al.Design and implementation of 10－Gigabit Ethernet MAC controller based on FPGA ［J］.Computer Engineering and Applications，2012，48 （6）：77－79 （in Chinese）. ［张友亮，刘志军，马成海，等.万兆以太网MAC层控制器的FPGA设计与实现［J］.计算机工程与应用，2012，48 （6）：77－79.］

［4］Patane G Campobello，Russo M.Parallel CRC realization ［J］.IEEE Transactions on Computers，2003，52 （10）：1312－13l9.

［5］PENG Wei.Research on embedded system CRC algorithm design［J］.Journal of Nanjing University of Information Science ＆ Technology （Natural Science Edition），2012，4 （3）：258－265 （in Chinese）.［彭伟.嵌入式系统CRC循环冗余校验算法设计研究［J］.南京信息工程大学学报，2012，4 （3）：258－265.］

［6］Wong Y，Zhang H.Techniques for segmented CRC design in high speed networks：U.S.Patent 8，037，399 ［P］.2011－10－11.

［7］Ahmad A，Hayat L.Selection of polynomials for cyclic redundancy check for the use of high speed embedded：An algorithmic procedure ［J］.WSEAS Transactions on Computers，2011，10 （1）：16－20.

［8］Stavinov E.A practical parallel CRC generation method ［J］.Circuit Cellar－the Magazine for Computer Applications，2010，31 （234）：38.

［9］XU Zhanqi，PEI Changxing，DONG Huainan.Generalized CRC computation algorithm with multiple channels and its implementation［J］.Journal of Nanjing University of Posts and Telecommunications（Natural Science），2008 （2）：53－57 （in Chinese）.［徐展琦，裴昌幸，董淮南.一种通用多通道并行CRC计算及其实 ［J］.南京邮电大学学报，2008 （2）：53－57.］

［10］BI Zhankun，ZHANG Yimeng，HUANG Zhiping，et al.Study on CRC parallel algorithm and its implementation in FPGA ［J］.Chinese Journal of Scientific Instrument，2007，28（12）：2244－2249 （in Chinese）. ［毕占坤，张羿猛，黄芝平，等.基于逻辑设计的高速CRC并行算法研究及其FPGA实现［J］.仪器仪表学报，2007，28 （12）：2244－2249.］

［11］Ramabadran T V，Gaitonde S S.A tutorial on CRC computations ［J］.IEEE Micro，1988，8 （4）：62－75.

［12］LI Youmou，FANG Dingyi.Research and implementation of a new CRC coding algorithm ［J］.Journal of Northwest University（Natural Science Edition），2006，36 （6）：895－898 （in Chinese）.［李宥谋，房鼎益.CRC编码算法研究与实现 ［J］.西北大学学报 （自然科学版），2006，36 （6）：895－898.］

［13］ZHANG Shugang，ZHANG Suinan.CRC parallel computation implementation on FPGA ［J］.Computer Technology and Development，2007，17 （2）：56－58 （in Chinese）.［张树刚，张遂南.CRC校验码并行计算的FPGA实现 ［J］.计算机技术与发展，2007，17 （2）：56－58.］