联合法探测修复北斗系统测量数据周跳
栗衍报,武海波,焦 建,王民昌
(1.山东省公路建设集团有限公司,济南 250000;2.淄博博山市政园林局,山东 淄博 255200)
1 引言
周跳问题一直是导航定位中研究的热点问题之一,目前存在很多种周跳探测修复方法,例如电离层残差法、Kalman滤波、M-W组合、多普勒积分法等[1-7]。这些方法各具特点但是也都存在一定缺点,例如电离层残差法可以高效地探测小周跳但却无法修复周跳以及无法正常探测出某些特定组合的周跳;M-W组合可以探测出比较大的周跳,但是受伪距质量影响严重等。
自1992年Canon提出多普勒积分法探测修复周跳以来,多普勒积分法已经广泛应用于全球定位系统(global positioning system,GPS)中的周跳探测。多普勒观测常量受卫星与地球的几何距离变化影响严重。由于GPS卫星都为中圆地球轨道(medium earth orbits,MEO)卫星,而我国北斗卫星导航系统(BeiDou navigation satellite system,BDS)卫星中含有5颗地球静止轨道(geostationary earth orbits,GEO)卫星。GEO卫星多普勒观测常量相较于GPS波动更大,因此无法像GPS那样简单地通过对多普勒常量取整来探测修复周跳。
2 方法介绍
2.1 电离层残差法周跳探测原理
电离层残差法利用载波双频数据进行线性组合,得到B1,B2载波中周跳的线性组合值和电离层残差高阶项,通过对此线性组合值设定阈值并判断是否超出阈值,以此来探测周跳。电离层残差检验方程为[8]

式(1)中,φ(t)与φ(t+Δt)分别为t时刻与t+Δt时刻载波无电离层组合值,f1、f2分别为B1、B2载波的频率,a1、a2分别为B1、B2载波在t时刻与t+Δt时刻的周跳,与分别为t时刻与t+Δt电离层残差高阶项,在采样率较高的情况下,在0附近波动。
由于电离层残差高阶项为极小的值,在采样率较高时可以忽略不计,因此在没有周跳的情况下,Δφ应当接近于0。但是实际情况中,考虑到观测噪声的影响,Δφ的限差一般设为±0.07周。即当时,认为不存在周跳。但是针对一些特定的周跳组合,即的组合,电离层残差法无法探测出周跳的存在。
经分析发现,在有周跳的情况下,上述情况出现的概率为0.25%,虽然出现的概率并不大,但由于这些周跳组合都是大周跳,因此,在定位中的影响非常大。
2.2 多普勒积分进行周跳探测原理
在GPS研究领域中,早已有人提出利用多普勒积分进行周跳探测[9-10]。在采样率较高时,GPS卫星的多普勒频率在历元间变化量很小,因此可以通过直接计算历元间多普勒积分并进行取整来探测修复周跳[11]。利用多普勒积分进行周跳的探测与修复的模型为[12]

式(2)中,ΔN为周跳检验量,D表示多普勒观测值(单位分别为周和Hz)。
由于给出的模型用相邻两个历元多普勒观测常量的平均值与时间的乘积代替多普勒观测常量在相邻两个历元的积分,因此,利用多普勒积分探测周跳是建立在相邻两历元多普勒观测常量变化不大的基础之上的。
BDS卫星中G01~G05为GEO卫星,受到轨道高度与卫星与地球径向速度的影响,GEO卫星的多普勒观测常量相较于GPS历元间变化更大。
如图1、图2及图3分别是C01(GEO)卫星和倾斜地球同步轨道(inclined geo-synchronous orbits,IGSO)C10卫星的B1载波和GPS中G05卫星的L1载波的多普勒观测常量的变化规律。不难发现,IGSO卫星的多普勒观测常量变化特征与GPS卫星相似,而BDS卫星中GEO多普勒观测常量相较IGSO卫星和GPS卫星的多普勒观测常量历元间变化大的多,因此GEO卫星不应该像GPS卫星那样仅仅通过多普勒积分取整就断定是否存在周跳以及周跳的大小。
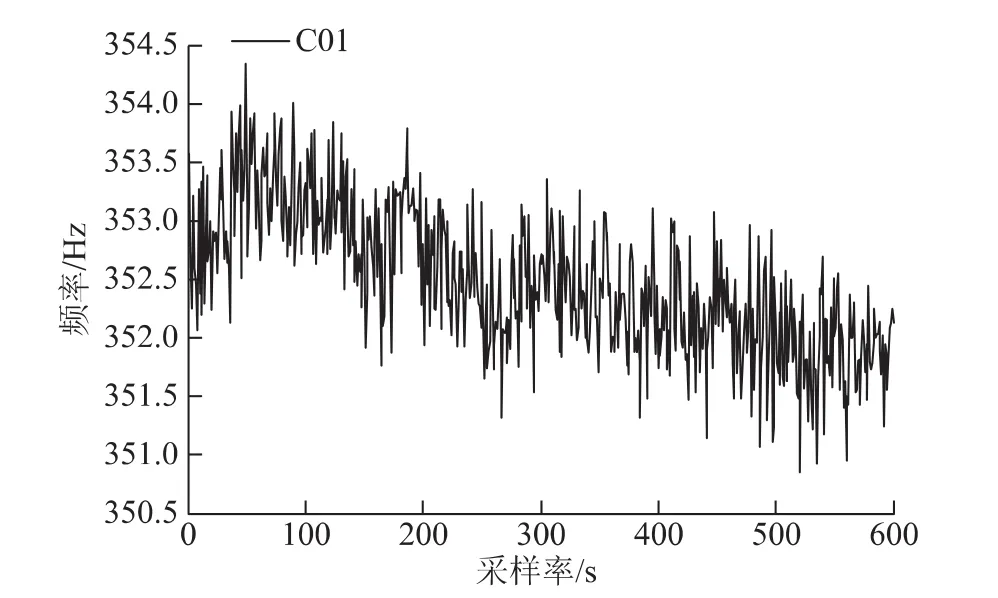
图1 C01(GEO)卫星多普勒频率时间序列图(1s采样率)
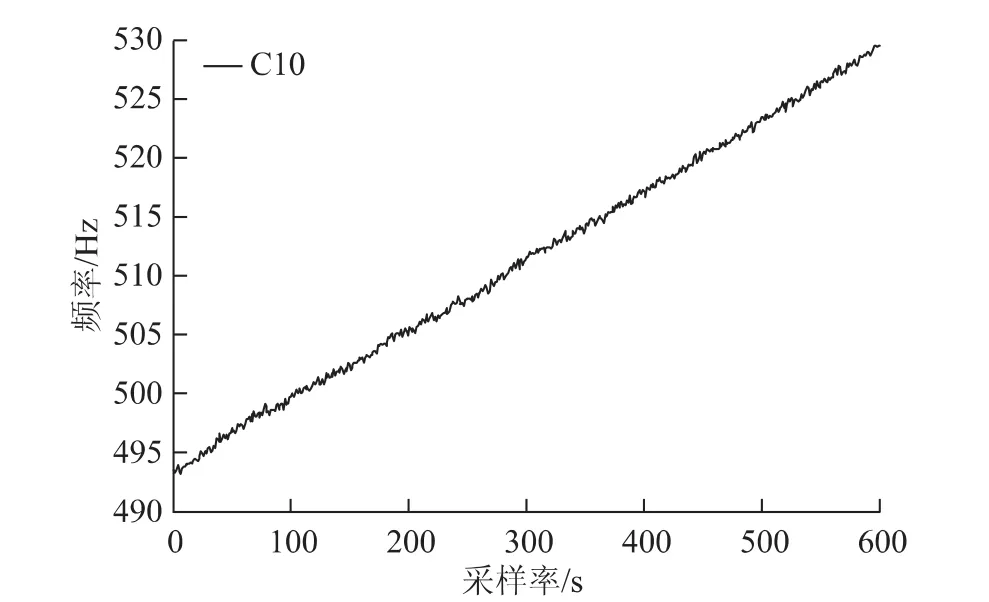
图2 C10(IGSO)卫星多普勒频率时间序列图(1s采样率)
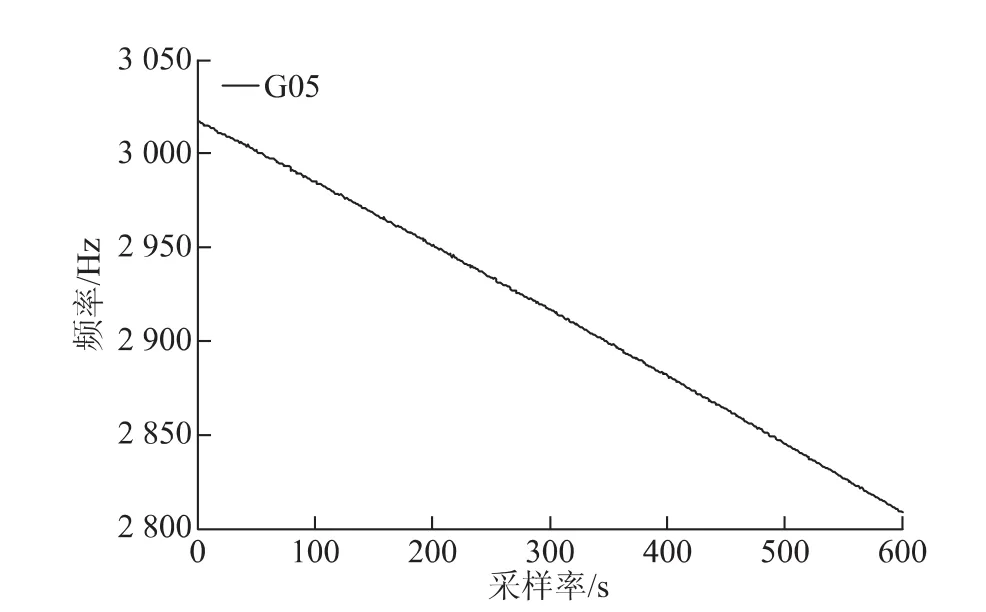
图3 G05卫星多普勒频率时间序列图(1s采样率)
2.3 电离层残差与多普勒积分联合探测周跳原理
众所周知,电离层残差法的优点在于其在采样率较高的时候能探测出很小的周跳,其缺点是对于某些特定的组合,例如对B1、B2载波分别为(9,7)、(18,14)、(27,21)的组合不能很好的发现周跳。而多普勒积分的特点是当相邻两历元多普勒观测常量变化较大时无法很好探测出周跳[13]。在实时差分定位过程中,通常使用采样率为1s的数据,在高采样率的情况下,将这两种方法的组合使用就能很好的探测并修复周跳。
3 实验验证
为了证明电离层残差和多普勒积分组合法能够很好的探测并修复周跳,笔者设计了一种电离层残差和多普勒积分组合法组合检测并修复周跳的方法,流程为图4所示。
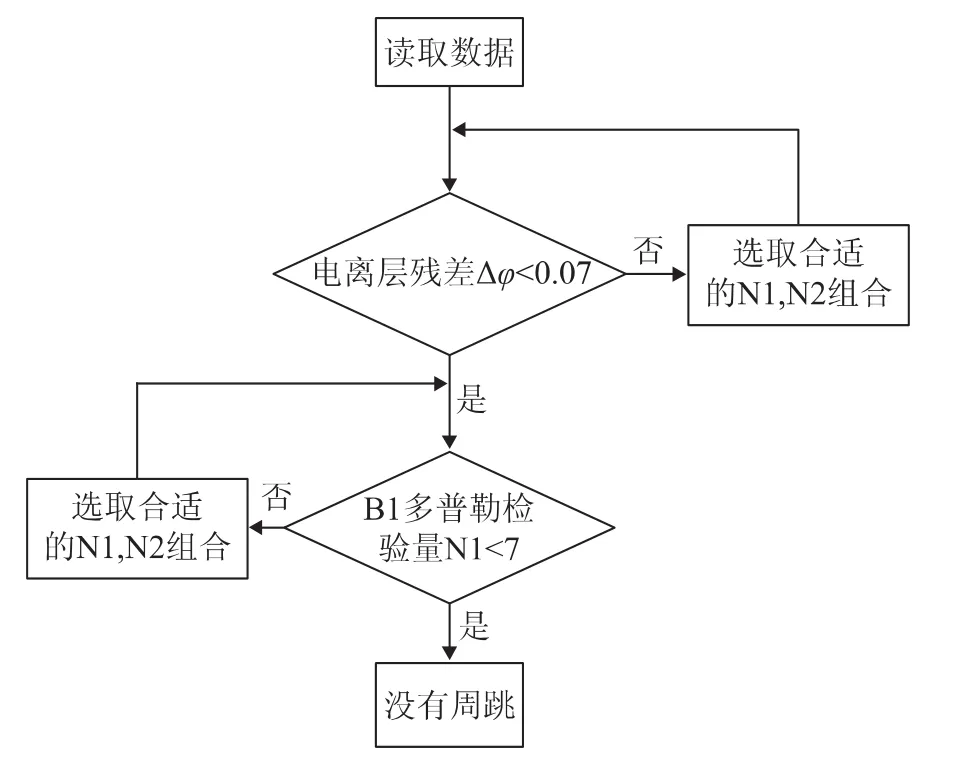
图4 电离层残差法与多普勒积分联合探测修复周跳
图4中的Δφ为电离层残差检验量,N1、N2分别为B1、B2载波周跳检验量。
电离层残差法与多普勒积分法组合探测周跳的过程是先用电离层残差法对数据进行处理,因为考虑到采样率为1s,电离层变化很小,因此将电离层残差法的阈值设为0.07,此时,进行检验时会出现两种情况:
(1)电离层残差法检测量出现大于0.07。这时认为检验数据中含有周跳。此时,用多普勒积分对B1,B2载波分别进行探测,将出现问题的历元检验量向下取整,求得N1,N2,由于在采样率为1s时,历元间多普勒积分检验量不会超过1,因此,在对B1,B2的检验量向下取整后,只需再用电离层残差法检验(N1,N2),(N1+1,N2)(N1,N2+1),(N1+1,N2+1)四组数据,求得修正后的周跳组合(N1’,N2’),这样就可以将周跳很好修复。
(2)电离层残差法检测量没有出现大于0.07。这时会有两种情况,第一种是B1和B2中都没有周跳出现。第二种是B1和B2中有粗差,这种情况不属于存在周跳,因此本文不予讨论。第三种情况是B1与B2中出现了前文中所说的周跳组合,例如(9,7)、(18,14)等,虽然经过分析这些组合出现的概率很低,但是一旦出现对定位影响极大。因此对电离层残差检测量大于0.07的数据再进行进一步处理。对B1载波进行多普勒积分探测周跳,由于能逃脱电离层残差法 “侦测”的数据在B1上周跳最小值为9,因此,设B1多普勒积分的阈值为7,若B1载波的多普勒积分的检测量大于7,则证明肯定有前文所说的周跳组合,这时对B1载波进行多普勒积分,将检验量向下取整得到N1,将N1与9n(n=0,1,2,3…)进行比较,取最接近的一个,进而求得N1的修正值N1’,同理,对B2载波也进行处理,得到修正值N2’,此时的(N1’,N2’)即为存在的周跳组合。
为了检测此方法的可用性,笔者于2013-05-07在南京六合地区采集了GPS+BDS双系统数据,接收机采用S82C双星四频接收机,数据时长为60min,采样率为1s。该时间段共有GPS卫星7颗,分别为 G14,G22,G31,G29,G12,G30,G32,BDS卫星共有8颗,分别为C01,C03,C04,C06,C07,C08,C09,C10。为了证明在该时间段没有发生周跳,利用另一台S82C双星四频接收机与测试用接收机组成10m短基线,通过对事后数据进行基线解算,并通过分析残差值,得到固定解标准差为0.002 89m,因此可以认为该时间段内没有发生周跳,即该时间段的数据为“干净数据”。
图5~图8列举了其中一个测站的部分BDS卫星的载波观测数据。
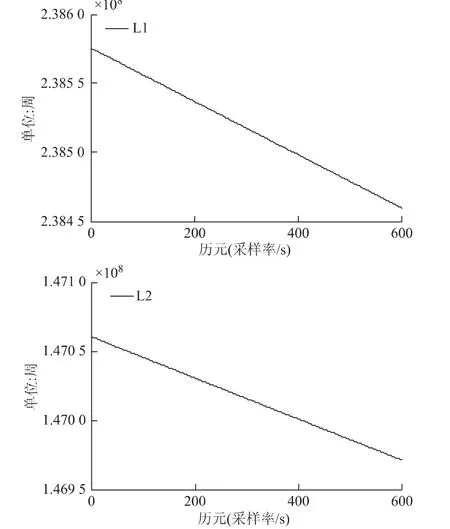
图5 观测时间段C01号卫星载波观测值
图5~图8为列举的C01、C03、C08以及C10号卫星的载波观测值。从BDS卫星中选取一颗GEO卫星(C01)与一颗IGSO卫星(C08)的观测值检验此方法的有效性。对0~600历元 “干净数据”人为加入模拟周跳,在第100、200、300、400历元处分别加入周跳为(1,0)、(2,1)、(9,7)、(18,14)的四组周跳组合,表1记录下GEO卫星的周跳探测与修复,表2记录下IGSO卫星的周跳探测与修复。
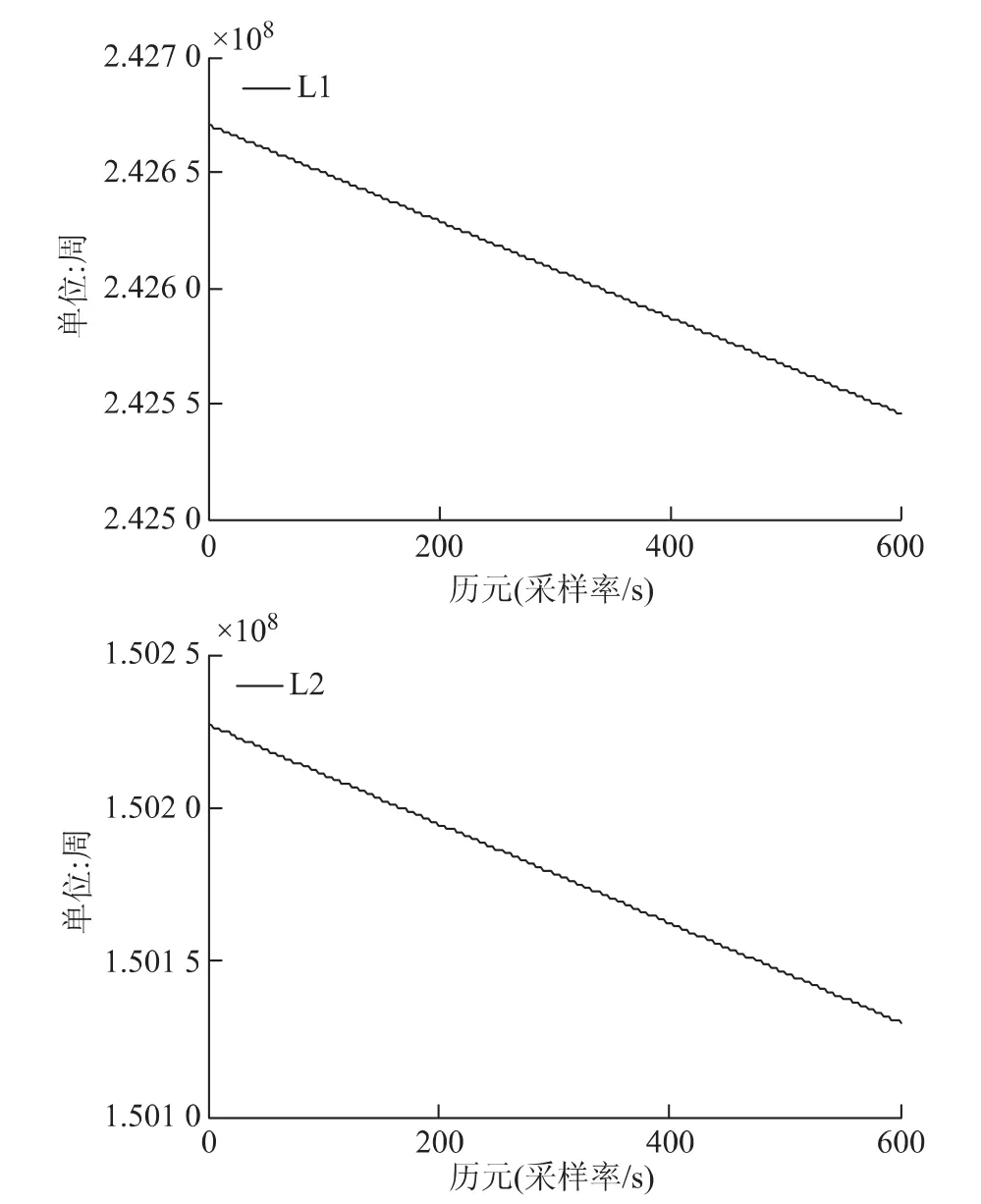
图6 观测时间段C03号卫星载波观测值

图7 观测时间段C08号卫星载波观测值

图8 观测时间段C10号卫星载波观测值
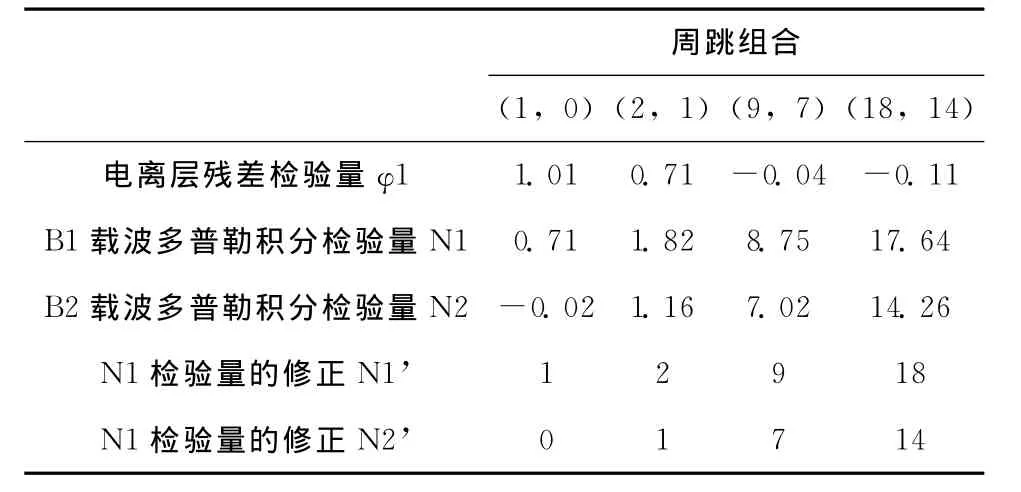
表1 1s采样率时GEO卫星电离层残差法与多普勒积分联合探测周跳 (单位:周)
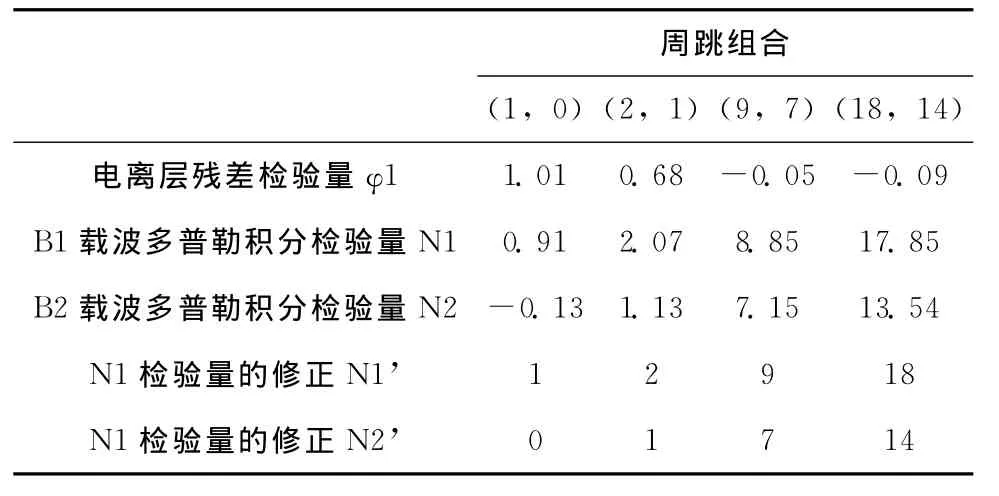
表2 1s采样率时IGSO卫星电离层残差法与多普勒积分联合探测周跳 (单位:周)
经过实验分析,无论是对于GEO卫星还是IGSO卫星,电离层残差法与多普勒积分法联合探测修复周跳都能快速探测并修复出现的周跳。电离层残差法弥补了多普勒积分不能精确确定GEO中周跳大小的缺点,而多普勒积分则通过电离层残差法的 “过滤”组合出正确的周跳,因此,这两种方法互相弥补了各自的缺点。
4 结束语
本文通过分析BDS卫星多普勒观测常量的变化特点以及电离层残差法与多普勒积分的互补性,提出了基于电离层残差和多普勒积分联合探测周跳的方法,进而分析了此方法的原理与流程设计,最后通过实验验证其可行性。实验证明,当BDS卫星中出现周跳时,无论周跳大小与何种组合方式,电离层残差与多普勒积分组合法都能快速有效地探测并修复周跳。
[1]生仁军.GPS载波相位定位中周跳探测方法的研究[D].南京:东南大学,2006.
[2]何海波,杨元喜.GPS动态测量连续周跳检验[J].测绘学报,1999,28(3):228-240.
[3]周巍,郝金明,贾小林.几种周跳探测方法在COMPASS数据处理中的应用[J],测绘工程,2009,18(2):66-69.
[4]冯威,廖华,黄兴干,等.一种改进的载波载波相位周跳探测与修复方法[J].测绘科学,2010,35(6):39-41.
[5]孙保琪,欧吉坤,圣传贞,等.一种适于Compass周跳探测的三频数据优化组合[J].武汉大学学报:信息科学版,2010,35(10):1157-1160.
[6]罗腾,白征东,原波.北斗三频组合数据在周跳探测和修复上的应用[J].测绘科学,2011,36(6):167-168.
[7]罗腾,白征东,过静珺.两种周跳探测方法在北斗三频中的应用比较研究[J].测绘通报,2011(4):1-3.
[8]徐园,杨力,耿彦龙.基于多频载波/伪距组合进行周跳探测与修复的实现[J].测绘工程,2012,21(3):49-52.
[9]王伟亮.网络RTK关键算法及CORS系统完备性监测研究[D].南京:东南大学,2012.
[10]李锋.多普勒频率测量技术研究与工程实现[D].长沙:中南大学,2011.
[11]雷雨,高玉平.双频相位求差法与多普勒法探测与修复周跳的比较[J].测绘工程,2010,19(3):10-13.
[12]常志巧,郝金明,李俊义.利用多普勒观测检测周跳和粗差[J].测绘通报,2008(3):28-30.
[13]陈远,于兴旺,叶聪云,等.GPS多普勒观测值测速的精度分析[J].全球定位系统,2008(1):31-34.
——卡文迪什测定万有引力常量

