基于FEM的鱼雷低频振动环境预示方法研究*

(1.中国船舶重工集团公司第705研究所 西安 710075)(2.水下信息与控制重点实验室 西安 710075)

基于FEM的鱼雷低频振动环境预示方法研究*

马锐磊1,2尹韶平1,2曹小娟1严海1秦晓辉1

(1.中国船舶重工集团公司第705研究所 西安 710075)(2.水下信息与控制重点实验室 西安 710075)

针对鱼雷设计初期振动试验条件制定所需实测数据不足的问题,论文采用有限元法对鱼雷典型部位低频振动环境进行预示:运用MSC.Nastran对先期建立的全雷有限元模型进行模态分析,并与试验数据对比的结果说明了模型的准确性;以实测振动加速度谱作为激励,对雷体典型部位的振动量级进行预示,总振动级结果与试验差值在±3dB以内;加速度谱线主要峰值吻合度较高,趋势基本一致。通过试验验证说明了该方法的有效性,可以为鱼雷低频振动试验条件的制定提供理论支撑。

模态分析;振动响应分析;环境预示;仿真

ClassNumberU663

1 引言

鱼雷是一种涉及机械、电子、力学、动力、控制、水声、爆炸等多学科的高技术水下精确制导武器。由于使用平台多样,在其全寿命周期内要经历运输、装载、贮存、空中飞行、入水、水下航行等多个环节,所经历的振动环境十分复杂。

如设计不当,环境适应能力不强,在使用中会出现某些零部件或电子元件破坏,导致鱼雷不能正常工作,严重时还会危及到携带平台的安全[1]。因此,充分了解鱼雷的环境特点,分析各环境因素对鱼雷的影响,提出合理的环境试验条件,是鱼雷研制中重要而不可或缺的工作内容。

为了满足新产品的设计需要,试验条件必须在缺乏新产品的实测环境数据条件下完成,所需的环境只能靠环境预示解决。因此,环境预示的准确性将直接影响试验条件的合理性。

在航空航天领域,振动环境预示技术发展迅速,得到大量研究成果。Ali[2]、Tsoi[3]等利用耦合有限元/边界元方法计算卫星天线结构在混响声场作用下的动力学响应,Yarza[4]等利用VA One软件的有限元/边界元方法,计算固支状态卫星反射天线结构在混响声场中的加速度响应,都得到了较好的结果。国内学者[5]也开始应用商业软件中的有限元/边界元方法开展典型结构在噪声激励下的响应分析研究。

但是,目前国内在制定鱼雷型号振动试验条件时多是在参考军用标准或同类产品研制经验的基础上,对相关标准进行剪裁而得出。所制定的试验条件往往与鱼雷所承受的实际环境条件有较大差别。因此,迫切需要开展鱼雷振动传递特性研究,在综合分析试验测试结果的基础上,进行鱼雷振动环境条件的预示,为科学制定环境试验条件提供理论依据。

本文采用有限元法(FEM),建立鱼雷结构振动响应计算模型,运用Nastran对其进行自由状态下的模态分析,通过试验数据验证模型的准确性。然后以实测的振动试验数据作为输入条件,计算雷内特征部位的振动响应值,研究在少量外载荷振动数据条件下,分析鱼雷各组件的振动环境,并研究舱段及关键部位的鱼雷低频振动环境试验条件预示方法。研究成果可以为制定鱼雷振动试验条件提供理论依据。

2 模态理论

结构系统模态分析的核心内容,就是通过计算或试验的方法,确定用来描述结构系统特性的固有频率、阻尼比和振型等模态参数[6]。在数学上,就是求解结构动力学方程的特征值或广义特征值的问题。结构系统的动力学方程通常可以表示为

(1)

略去结构系统的运动微分方程中的阻尼力项和外载荷项,得到系统无阻尼自由振动的动力学方程:

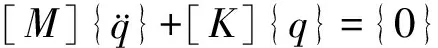
(2)

令式(2)的解为

{q}={A}sin(ωt+φ)

(3)

式中:{A}为振幅,由初始条件决定;φ为相位角,由初始条件决定;ω为固有频率,由系统固有特性决定。

代入式(2)可得

([K]-ω2[M]){A}sin(ωt+φ)=0

(4)

由于{A}≠0,有

|[K]-ω2[M]|=0

(5)

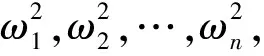
3 有限元建模及模态验证

3.1 全雷有限元建模

鱼雷由自导头段、操雷段、电子舱段、燃料舱段、动力舱段及尾段组成,建模总体思路是先建立舱段模型,然后将各舱段模型整合成全雷模型。建模时,首先将几何模型导入有限元前处理软件HyperMesh中,忽略模型中小孔、倒角等微小特征。对鱼雷薄壳体,有限元建模时按结构的力学功能[7]可把鱼雷壳体简化为2D shell板壳单元[8];环向加强筋可用1D beam梁单元建模;一些零部件对全雷刚度矩阵影响很小,但对全雷的质量矩阵影响很大[9],可用0D质量元建模。全雷模型如图1所示,整个模型单元总数为48188个,节点总数50441个。

图1 全雷有限元模型

3.2 模态验证

将模型文件以bdf格式导入MSC.Nastran中进行模态计算,选用兰索斯(Lanczos)法求解。其一阶、二阶及三阶模态的固有频率分别为27.9Hz、55.1Hz和88.6Hz。

为验证模型仿真计算的精确度,进行了全雷模态试验,模型仿真计算固有频率值与试验结果对比情况见表1,模态振型对比结果如图2～图5所示。

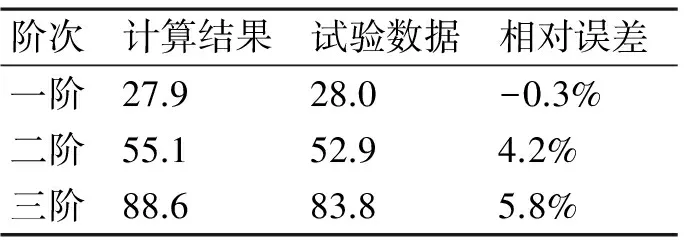
表1 试验与仿真结果对比(单位:Hz)

图2 试验第一阶振型

图3 计算第一阶振型

图4 试验第二阶振型

图5 计算第二阶振型

从有限元仿真与试验结果对比,可以看出:二者模态振型基本一致,仿真计算的固有频率值与试验数据相对误差控制在6%以内,满足工程计算要求,说明了模型的准确性。为后续振动响应分析提供支撑。

4 振动环境预示方法

振动环境预示是在综合分析产品环境剖面的基础上,准确获取产品受到的激励条件,通过特定方法得到产品特征部位的振动响应数据,进而制定出产品的振动试验条件。

目前振动环境预示方法主要有三种:外推法、统计能量法和有限元法。外推法由于不能对系统整体结构进行预示;无法给出结构的详细频率特性以及不能用于联合激励下的环境预示等限制,应用范围有限。统计能量法从能量角度对系统进行分析,不依赖于系统参数,主要应用于模态密集的高频系统振动环境预示。对于低频振动环境,主要通过有限元动力学响应计算的方法进行预示,该方法的关键是建立一个准确的振动分析模型,在此基础上,分析激励振源并选择激励输入的形式(例如加速度、功率谱及力等),确定振动响应输出点,对结构中难以得到测量数据的典型位置的振动量值进行预示,通过对不同工况下结构振动特性的分析,得到最为恶劣工况下的振动响应数据,提出初步的振动试验条件指导设计工作,并在后续试验基础上不断优化。

5 振动响应分析

本文针对鱼雷低频(1Hz～1kHz)振动环境进行预示,选择有限元振动响应计算方法。根据鱼雷实航试验数据,以发动机舱后隔板为激励源;以实测振动加速度谱为输入,对鱼雷尾段、燃料舱段壳体及尾段舵机安装基座1kHz频段内的振动响应进行了分析计算,通过与实际测试数据对比,验证了预示方法的有效性。

5.1 输入激励

模型中激励点的位置如图6所示,根据试验测点的布置情况约束激励点轴向及径向。输入载荷的加速度频谱曲线如图7～图8所示,频率分辨率为1Hz,频率范围为1Hz～1kHz。

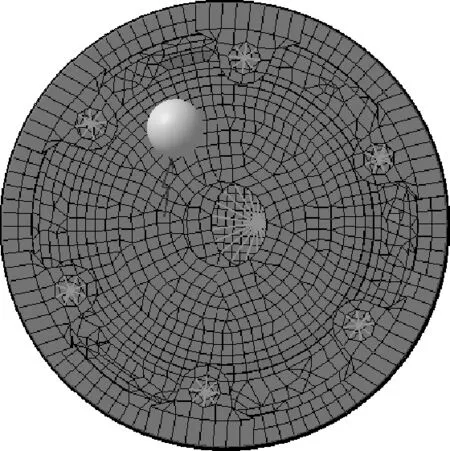
图6 激励点位置

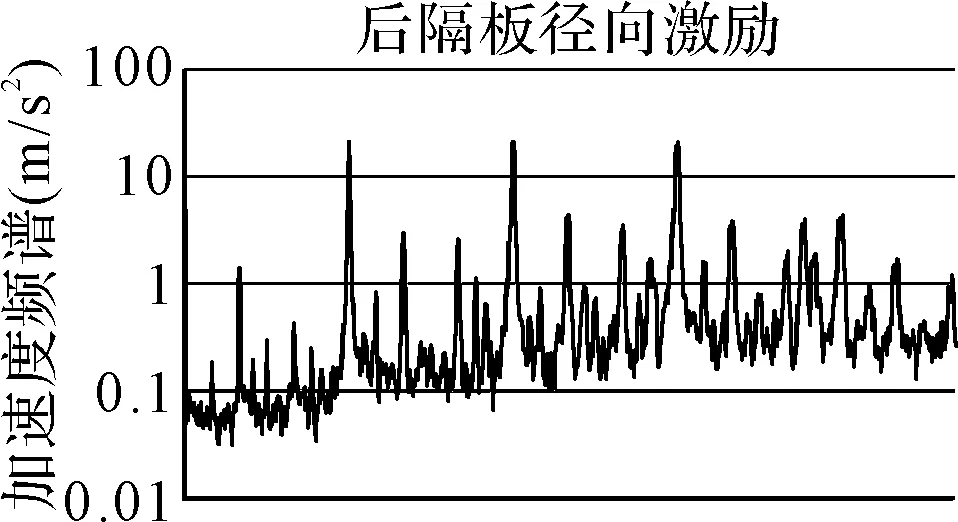
图8 径向激励谱线

5.2 输出响应点

发动机激励产生的振动最终传递到鱼雷各舱段的壳体及组件上,引起相应部位的振动响应。本文选取燃料舱壳体、尾段壳体及舵机安装基座三个典型输出响应点进行计算。测点位置如图9～图10所示。

图9 壳体输出响应点位置

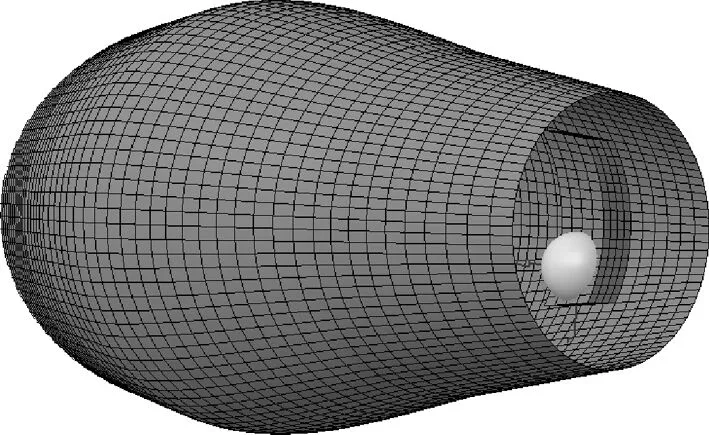
图10 舵机安装基座输出点位置

5.3 结果验证

采用模态叠加法[10]求解结构输出点的加速度响应谱,通过有限元计算结果与试验数据的对比验证计算方法的有效性。1kHz频段内总振动级对比结果如表2所示,仿真计算与试验谱线对比结果如图11～图13所示。

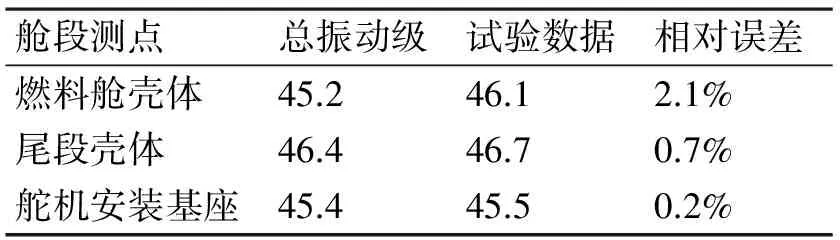
表2 试验与仿真结果对比(单位:dB)

图11 燃料舱壳体谱线对比

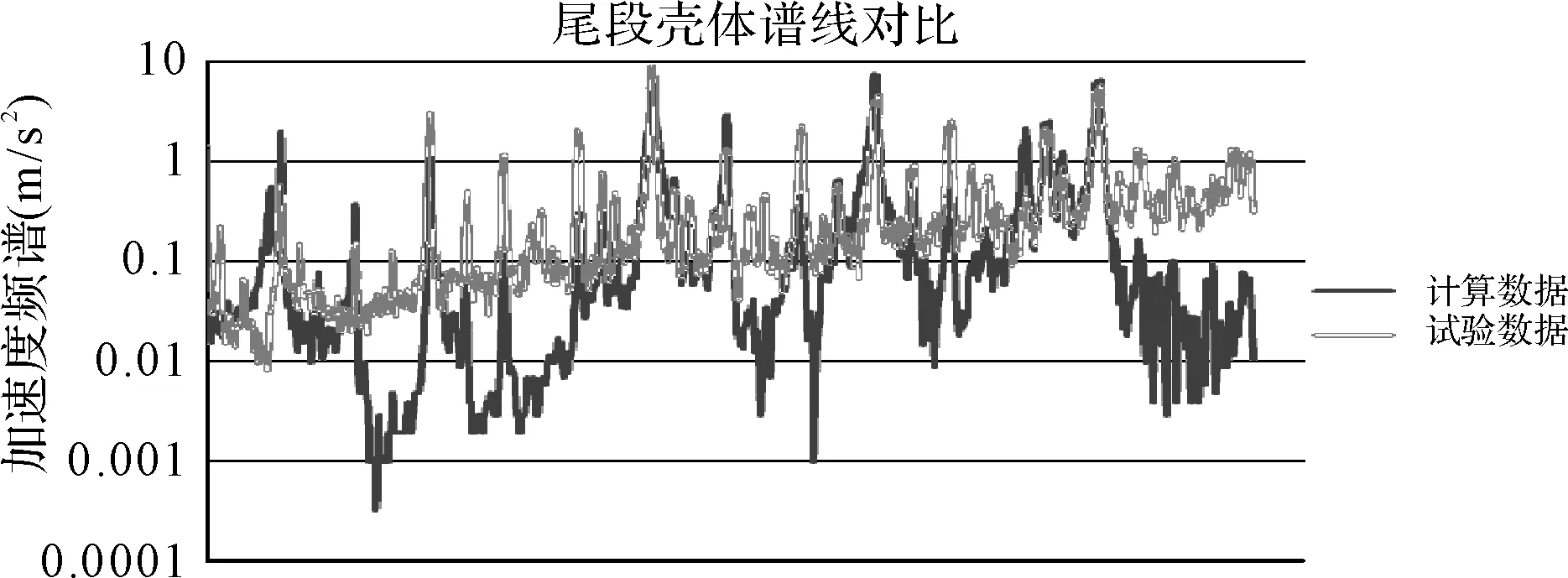
图12 尾段壳体谱线对比

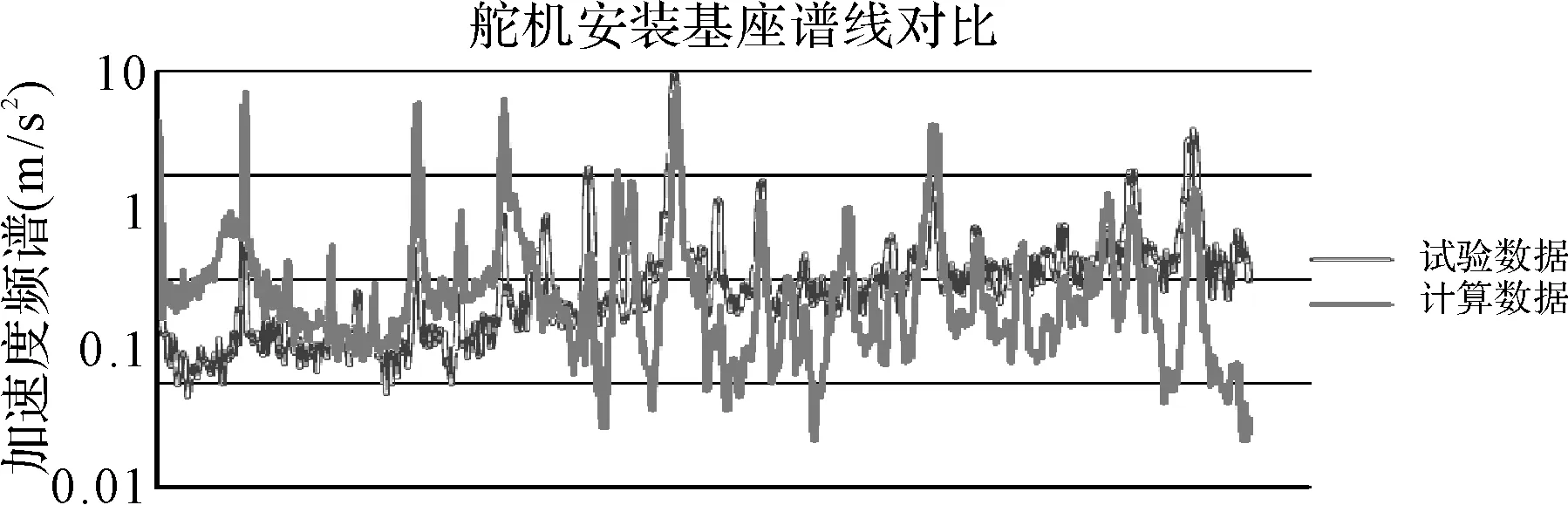
图13 舵机安装基座谱线对比

从对比结果情况可以看出:仿真计算与试验总振动级差值在±3dB以内,相对误差在2.1%以内;谱线中各主要峰值点吻合度较高,谱线总体趋势基本一致。这是由于采用模态叠加法,所建的有限元模型较好地模拟了实际结构,所以结构测点在一些主要模态上频率比较接近。

计算谱线与试验有一些差异可能的原因是:

1)鱼雷在运行过程中,所受振动环境复杂,存在许多激励源。实际上,雷体工作中的振动响应是所有激励源共同作用的结果。

2)仿真计算时,激励点位置选择不可能与试验中的测量点完全重合,由此带来一定的误差。

3)有限元模型与实际结构不可避免地存在一定差异,导致结果存在误差。

6 结语

1)通过全雷有限元仿真计算与试验数据的对比说明了模型的准确性,为振动响应计算提供模型支撑。

2)通过有限元振动响应分析,以加速度谱为激励,对鱼雷典型部位的振动响应进行了计算,与试验测试数据对比表明:谱线中各主要峰值点吻合度较高,谱线总体趋势基本一致;总振动级差值在±3dB以内,相对误差在2.1%以内。说明通过有限元振动响应分析的方法对鱼雷低频振动环境进行预示是有效的。此方法可以为鱼雷振动试验条件制定提供理论支撑。

[1]尹韶平,刘瑞生.鱼雷总体技术[M].北京:国防工业出版社,2011.

[2]Kolaini A R, Kissil A, Childs B W. Vibro-acoustic analysis of lightweight structures[C]//The 2009 S/C&L/V Dynamic Environment Workshop, El Segundo, USA,2009.

[3]Tsoi W B, Kolaini A R, Childs B W. Acoustic induced vibration on composite reflector:test versus prediction[C]//The 2008 S/C&L/V Dynamic Environments Workshop, El Segundo, USA,2008.

[4]Yarza A, Castro O, Santiago-Prowald J, et al. Reflector vibroacoustic response to launch acoustic excitation[C]//European Conference on Antennas and Propagation 2010, Barcelona,2010.

[5]韩峰,胡迪科,闫桂荣.圆锥壳结构声振耦合特性分析[J].噪声与振动控制,2009,29(5):30-33.

[6]姚熊亮.结构动力学[M].哈尔滨:哈尔滨工程大学出版社,2007.

[7]温熙森,陈循,等.机械系统建模与动态分析[M].北京:科学出版社,2004.

[8]张宇文.鱼雷总体设计原理与方法[M].北京:高等教育出版社,1997.

[9]Lau. Sunny G. Elastoplastic analysis for severe underwater explosions using dynamic finite element modeling[R]. Report documentation page,2004.

[10]杜骊刚.飞行器在气动噪声作用下的振动环境预示方法[J].装备环境工程,2008,5(6):65-67.

Torpedo’sVibrationEnvironmentPredictionMethodofLowFrequencyBasedonFEM

MA Ruilei1,2YIN Shaoping1,2CAO Xiaojuan1YAN Hai1QIN Xiaohui1

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710075)

(2. Science and Technology on Underwater Information and Control Laboratory, Xi’an 710075)

To solve the problem of lacking of test data before establishing guideline for environmental test. A method of torpedo’s vibration environment prediction of low frequency is proposed. Modal analysis of torpedo under free-free state based on the finite element model built up earlier and the analysis of the torpedo’s vibration response exited by acceleration spectrum lines are carried out by using MSC. Nastran. The comparison results between simulation and modal testing indicate that the global vibration level was in ±3dB, and the spectrum lines were similar. Therefore, the validity of the vibration environment prediction method using finite element model is verified.

modal analysis, analysis of vibration response, vibration environment prediction, simulation

2013年11月4日,

:2013年12月10日

马锐磊,男,硕士研究生,研究方向:武器系统总体技术。

U663DOI:10.3969/j.issn1672-9730.2014.05.038