求解0－1背包问题的两种算法设计*

刘朝霞

(集宁师范学院数学系，内蒙古 乌兰察布 012000)

背包问题(Knapsack problem)是由Merkel和Hellman在1978年提出的，后来通过对其特点的研究，表明该问题是一个典型的NP－complete问题。它被广泛应用在各种工业场合中，如资本预算、货物装载和存储分配等问题，这些问题都可以转化成0－1背包问题，因此研究0－1背包问题的求解方法具有非常重要的现实意义［1］。

0－1背包问题可描述为:有n个物品和一个背包。物品 i的价值为 vi，重量为 wi(i=1，2，…，n)，背包的容量为jmax。如何在n个物品中选取若干件装入背包，使其在背包容量许可下所装入的物品总价值最大?本问题中，对于任意第i个物品只存在装入背包和不装入背包两种选择，用xi表示对物品i做出选择的情况，当xi=0时，表示放弃物品i，即该物品没有装入背包;当xi=1时，表示选择物品i装入背包，需要说明的是同一物品只能装入背包一次，也不能只装入物品的一部分。0－1背包问题由此而得名。

1 0－1背包问题的数学模型

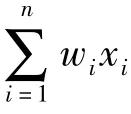
目前，求解0－1背包问题主要有精确算法和近似算法两种方法。精确算法有分支限界法、动态规划法等，近似算法有贪心法、群蚁算法、模拟退火算法等［2］。由于0－1背包问题具有最优子结构性质，满足贪心算法和动态规划算法对求解问题的要求，因此本文就采用动态规划法和贪心法求解0－1背包问题。

2 求解0－1背包问题的算法

2.1 动态规划算法(DP)

动态规划主要针对最优化问题，是求解决策过程最优化的数学方法。是在20世纪50年代初，由美国数学家R.E.Bellman等人在研究多阶段决策过程的优化问题时提出的，动态规划算法通常用于求解某种最优性质的问题，分治和解决冗余是其基本思想，将待求解的问题分解为规模大致相同、不相互独立的若干子问题，然后对各子问题进行求解，最终产生一个整体最优解［3］。

2.1.1 动态规划法求解0－1背包问题的算法设计

使用动态规划法进行算法设计，需要推导一个最优值的递归关系式。假设m［i］［j］是一个前i－1个物品已经做出选择的0－1背包子问题

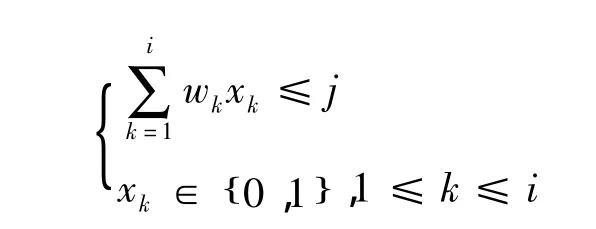
的最优值，即

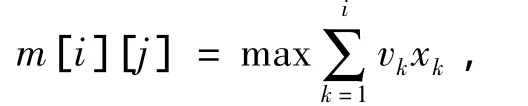
因为已经对前i－1个物品做出了选择，即序列(x1，x2，...，xi－1)已被确定。在选择第 i个物品时有如下两种情况之一:

(1)背包剩余容量不足以装入物品i，即j＜wi时xi=0，背包的价值不增加，最大价值

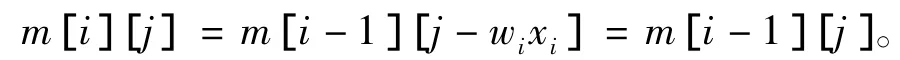
(2)背包容量能够装入物品i，即j≥wi时，若选择物品i装入背包，xi=1，则背包的价值增加vi，

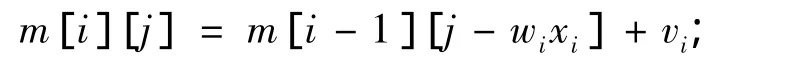
若选择物品i不放入背包，xi=0，则m［i］［j］=m［i－ 1］［j］。所以，当j≥wi时，对有i个物品的0 － 1背包子问题的最优解为二者的最大值。由此可得到如下递推关系式:

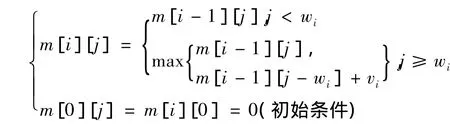
2.1.2 C++语言描述的算法实现

2.2 贪心法求解0－1背包问题

贪心法是一种简单、高效的算法设计策略，它总是从问题的一个初始解出发，每一次都根据贪心策略做出当前最优的选择，通过一次次的局部最优解，逐步逼近给定的目标，达到最终的整体最优解，这种启发式的策略不能对所有问题都获得最优解，但在许多情况下，能得到最优解的近似解［4］。因此，在求解NP完全问题中该算法具有越来越重要的作用。

2.2.1 贪心算法设计

选择最优的贪心策略是使用贪心法求解0－1背包问题时首先要考虑的问题，最优的贪心策略能够使得到的解更接近最优解。本问题可选择的贪心策略有三种:

第一种是价值最大贪心策略:在背包容量许可的情况下选择价值最大的物品装入，直到受到背包容量限制装不下为止。

第二种是重量最小贪心策略:在背包容量许可的情况下选择重量最小的物品装入背包，直到背包装不下剩余的物品为止。

第三种是价值重量比贪心策略:在背包容量许可的情况下选择vi/wi值最大的物品装入，直到背包装不下剩余的物品为止。

选择策略1，如果价值最大的物品重量太大，这样背包的容量得不到有效利用。选择策略2，如果重量小的物品价值也很低，这样很难保证背包的价值最大。策略3，既考虑了价值又考虑了重量，直观上，按该种策略可能得到最优解。本文就选择贪心策略3作为最优贪心策略来设计0－1背包问题的算法。

用贪心策略3求解0－1背包问题的步骤如下:求出给定物品的价值重量比vi/wi(i=1，2，...，n);将物品按照价值比重的非递增顺序进行排序;重复下面的步骤，直到不满足条件为止:将价值重量比最高的物品放入背包，计算背包的剩余空间，若当前背包剩余容量能够装入物品则装入，否则，选择下一物品。

2.2.2 C++语言描述的算法实现

3 两种算法的分析与比较

由以上求解0－1背包问题的两种算法设计可知，动态规划法和贪心法求解0－1背包问题都具有可行性，但这两种算法又存在一定的其局限性。下面将从时间和空间复杂度、准确性等方面对这两种算法进行分析。

在运用动态规划法的算法实现KnapSack函数中，由于算法的基本语句是衡量算法运行时间的主要依据，为此，选定if(w［i］＜=j)作为基本语句，该语句之执行的次数n×jmax，所以，该算法的时间复杂性为O(n×jmax)。由此可见，当背包容量jmax较大、问题规模n较大时，算法需要的计算时间较多，例如，当jmax＞2n时，算法需要O(n×2n)的计算时间。所以，动态规划法适合于规模较小问题的求解，但能保证求解的正确性。

贪心算法的主要计算时间将耗费在对物品按照价值比重进行非递增排序上，由于本文使用快速排序来实现价值比重的排序，因此算法的时间复杂度为O(nlogn)。然而，贪心算法属于近似算法，虽然速度快，但不一定是最优解。如对于n=3，jmax=50，wi=(10，20，30)，vi=(60，100，120)，其中i=1，2，3的0－1背包问题，按照贪心策略3做选择，由于物品1的价值比重最大，应首选物品1装入背包，但事实上选择第二个物品才是本问题的最优解，体现了该算法的局限性。

4 结束语

求解0－1背包问题除了精确算法－动态规划法和近似算法－贪心法外，还可以用回溯法、分支限界法、蚁群算法、DNA算法、粒子群优化算法等算法。但由于0－1背包问题是一个NP问题，对于规模较大的0－1背包问题还没有找到一种最佳的求解方法，也就是说，现有的每一种智能算法都有不同程度的局限性，都是在一定范围内求解。因此，这就需要我们在原有算法的理论基础上进一步研究，不断地改进和优化算法，最终能找到求解0－1背包问题的最佳方法。

［1］王晓东.算法设计与分析(第二版)［M］.北京:清华大学出版社，2008.

［2］王秋芬，吕聪颖，周春光.算法设计与分析［M］.北京:清华大学出版社，2011.

［3］李北斗.关于0－1背包问题的算法研究［J］.计算机与数字工程，2008，(5).

［4］田烽楠，王于.求解0－1背包问题算法综述［J］.软件导刊，2009，(1).