一类时滞食饵-捕食者系统的稳定性研究
孙玉涛,常 郝,张子振,徐 勇
(安徽财经大学 管理科学与工程学院, 安徽 蚌埠 233000)
一类时滞食饵-捕食者系统的稳定性研究
孙玉涛,常 郝,张子振,徐 勇
(安徽财经大学 管理科学与工程学院, 安徽 蚌埠 233000)
种群动力系统的演化不仅依赖于系统的当前状态,还依赖于系统过去某一时刻的状态.基于此,本文研究了一类具有时滞和比率HollingⅡ型功能性函数的食饵-捕食者系统.以捕食者成熟时滞τ为参数,利用微分方程理论,分析了系统正平衡点的稳定性,并给出了系统产生Hopf分支的条件.结果表明,给定参数满足一定条件时,两种群的密度会产生周期性的变化,或者都保持一种稳定状态.
Hopf分支;食饵-捕食者系统;时滞;稳定性
1 引言
近年来,具有时滞、功能性响应、阶段结构、扩散运动等特性的食饵-捕食者系统模型得到了专家学者们的广泛关注和深入研究[1-2].文献[3]研究了种内相食捕食模型非常数正解的存在性,并以扩散系数为分歧参数,讨论了发自正常数解的分歧.文献[4]研究了具有时滞的食物链反馈系统的局部Hopf分支的存在性.文献[5]提出了一类具有改进的Lesile-Gower和HollingⅡ型功能性反应函数的食饵-捕食者系统模型.文献[6]在相应的功能性反应函数中引进时滞,并构造了相应的Layapunov函数,讨论了正平衡点全局稳定的充分条件.众多研究表明,在种群动力学中,随着种群间的相互作用时滞是不可避免的,并且时滞有时候会破坏系统平衡点的稳定性.基于此,本文以捕食者成熟时滞τ为参数,讨论如下系统的正平衡点稳定性以及Hopf分支的存在性,进而得到系统存在小振幅周期解的充分条件.
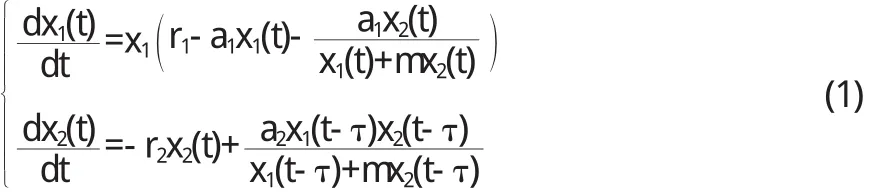
对于系统(1)x1(t)与 x2(t)分别表示食饵种群与捕食者种群在 t时刻的密度,r1=n1-n2表示食饵种群的内秉增长率,其中 n1为食饵种群的平均出生率,n2为食饵种群的平均死亡率,r2表示捕食者种群的死亡率表示食饵种群种内竞争系数,a1与 a2分别表示相应的转化率,m表示半饱和常数,t为非负,表示捕食者种群从幼年到成年的成熟时滞.系统(1)中各参数 r1,r2,a1,a2,m均为正常数.
作为预备知识,首先介绍如下定义:
考虑如下二维自治系统:

定 义 1 若(x0,y0)使 E(x0,y0)=0,F(x0,y0)=0,则称(x0,y0)为系统(**)的平衡点,如果 x0>0且 y0>0,则称(x0,y0)为系统(**)的正平衡点.
定义 2 设(x0,y0)为系统(**)的平衡点,且系统(**)在(x0, y0)处的线性化方程为:的所有特征值都具有负实部,则称系统(**)的平衡点(x0,y0)是渐近稳定的.

2 正平衡点的稳定性与周期解的存在性
定 理 1 如果系统(1)的参数满足下列条件:(T1)a2>r2且 mr1a2>a1(a2-r2),那么系统(1)有唯一的正平衡点.
证明 设 X(x*1,x*2)是系统的平衡点,则由系统平衡点的定义有:

解上述方程组可得系统 (1)的三个非负平衡点(0,0),,其中

本文只考虑系统(1)正平衡点的性态.系统(1)在正平衡点)处的一次近似系统为:

将系统(2)写为如下矩阵形式:

进而得到系统(2)的特征方程为:
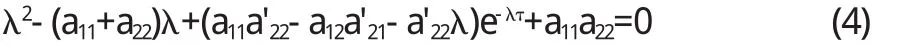
引理1如果系统(1)满足条件(T2)A+D>0,则当t=0时,方程(5)的根有严格负实部.
引理 2 如果系统(1)能同时满足引理 1中的条件与条件(T3)B<0且B2-C2<0,则方程(5)当 t=tk时有且仅有一对纯虚根±ie0,其中

证明 设 l=ie(e>0)是方程(5)的根,则将 l=ie(e>0)代入方程(5),并分离实部和虚部得:

上述两式平方相加得:

由引理条件易知,方程(6)有且仅有一个正实根 e0,此时方程(5)有一对纯虚根.
证明 对方程(5)两边同时对 t求导,得

进而,
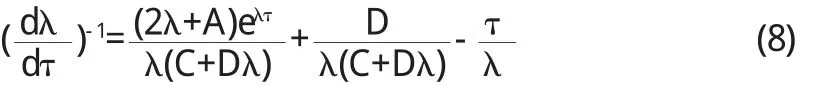

所以,

由引理(2)中的假设条件(T3)B2-C2<0,有
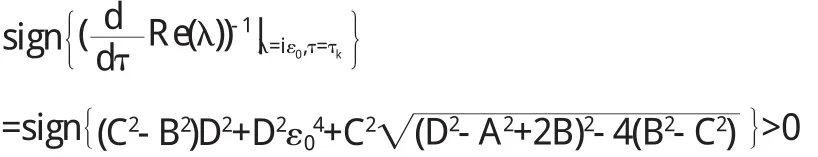
所以有

综合引理 1-3以及文献[9]中定理 11.1可以得到系统(1)的稳定性与 Hopf分支周期解的存在性定理.
3 结论
本文讨论了一类具有比率的 HollingⅡ型功能性函数以及捕食者具有成熟时滞的食饵 -捕食者系统.从以上分析所得的结果可知,捕食者的成熟时滞可以改变系统的稳定性,导致系统的不稳定性.当捕食者的成熟时滞比较小时,食饵种群和捕食者种群的密度都稳定在系统的正平衡点附近,整个系统保持一种静态的稳定状态;而当捕食者的成熟时滞比较大时,两种群的密度将发生周期性的变化,系统将保持一种动态的平衡.
〔1〕吴春光.一类捕食者-食饵种群动力学模型及数值模拟[D].北京:中央民族大学理学院,2009.
〔2〕孟笑莹,邓飞其,彭云建.具有随机扰动的食饵-捕食系统的稳定性[J].系统工程与电子技术.2011,33(2):385-389.
〔3〕查淑玲,李艳玲.一类种内相食捕食系统非常数正解的存在性[J].计算机工程与应用,2010,46(27):62-65.
〔4〕赵廷芳,卢梦霞,赵汇涛.一类三种群 食物链模型 正平衡解的稳定性与 Hopf分 支的存在 性[J].河南 大 学 学报(自 然科学版),2010,40(5):238-243.
〔5〕Nindjin A F,Aziz-Alaoui MA,Cadivel M.Analysis of a predator-prey model w ith modified Lesile-Gower Holling-type Ⅱschemes with time delay[J].Nonlinear Analysis:Real world Applications,2006,7(5):1104-79.
〔6〕张锦炎,冯贝叶.常微分方程几何理论与分支问题[M].北京:北京大学出版社,2005.
〔7〕史红波.扩散捕食系统正平衡态的定性分析[D].兰州:兰州大学,2010.
TP273;O141
A
1673-260X(2014)08-0007-02
安徽财经大学校级科研项目(ACKYQ1229);安徽省教育厅自然科学基金项目(KJ2011B002)

