一类非线性薛定谔方程组无穷多解的存在性
董静,魏公明
(上海理工大学理学院,上海200093)
一类非线性薛定谔方程组无穷多解的存在性
董静,魏公明
(上海理工大学理学院,上海200093)
讨论了一类非线性薛定谔方程组无穷多解的存在性.在假设的V(x),b(x),f(x)条件下,通过减弱喷泉定理的条件,运用变形的喷泉定理,证明了相关方程组的无穷多解的存在性.较扰动方法更加简捷.
薛定谔方程组;无穷多解;变形的喷泉定理
1 引言
主要考虑如下薛定谔方程组:
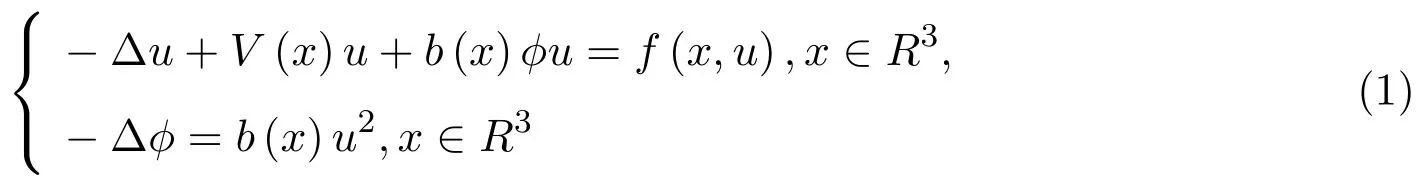
无穷多解的存在性.对于此类具有物理背景的方程组,受到了许多国内外学者的关注和研究,其中不乏许多已经得到的新的结果.当b(x)=1时,在文献[1]中作者证明了无穷多解的存在性:当V≡1,f(x,u)=|u|p−1u,1 在方程组(1)中,假设可能的V(x),b(x)和非线性项f(x)满足以下条件: (V1)V∈C(R3,R),infx∈R3V(x)≥a1>0(a1是正常数),对任意的M>0,有 (f1)|b(x)(| (f2)f∈R3×R,存在a2>0,p∈(2,2∗),|f(x,u)|≤a2(1+|u|p−1),x∈R3,u∈R,其中2∗是在维数为3的sobolev空间的一个临界指数,且f(x,u)u≥0,u≥0; (f5)对任意∈R3,G(x,s)≤G(x,t),∀(s,t)∈R+×R+,s≤t,定义:其中 定理1.1若(V1)成立,且f满足(f1)-(f6),则(1)式有无穷多个解{(uk,ϕk)},使得I(uk)→∞,即 2.1 一些符号说明 Ls(R3)是Lebesgue空间, H1(R3)是Sobolev空间, D1,2(R3)={u∈L6(R3)? ?∇u∈L2(R3)},其范数为 C:正常数; V(x)是有下界,对任意的s∈[2,2∗],E嵌入到Ls(R3)且是连续的; 对任意的u∈H1(R3),都存在唯一的ϕu(x)∈D1,2(R3),有−ϕu(x)=b(x)u2,ϕu的积分表达式为: 由此,可定义I:E→R 2.2 变形的喷泉定理 其中ρk>rk>0.考虑C1ϕλ函数:E→R,定义:ϕλ(u)=A(u)−λB(u),λ∈[1,2]. 假设如下: (F1)λ∈[1,2]时,ϕλ映射是有界集映射到一致有界集,ϕλ(−u)=ϕλ(u),对所有的(λ,u)∈[1,2]×E均成立, (F2)对所有的u∈E,都有B(u)≥0,当∥u∥→∞时,A(u)→∞或B(u)→∞.令对k≥2时,有 定理2.2.1[12]假设满足条件(F1)和(F2).如果对所有的λ∈[1,2],bk(λ)>ak(λ),那么ck(λ)≥bk(λ)(λ∈[1,2]),而且对任意的λ∈[1,2],存在一个序列有 定理2.2.2[12]如果C1函数E→R,定义:ϕλ(u)=A(u)−λB(u),λ∈[1,2]满足 (T1)ϕλ映射是λ∈[1,2]的有界集映射到一致有界集,同时ϕλ(−u)=ϕλ(u),对所有的(λ,u)∈[1,2]×E均成立, (T2)B(u)≥0,当∥u∥→∞时,B(u)→∞在任意有限维的子空间E中均成立, (T3)存在ρk>rk>0,存在: 则存在λn→1,u(λn)∈Yn,有 特别地,如果u(λn)对任意的k有一个收敛的子列,则ϕ1有无穷个非平凡临界点{uk}∈E{0}且满足ϕ1(uk)→0−(k→∞). 如果取E中的正交基{ej},令Xj=Rej,定义则可定义Iλ:E→R, 对所有的u∈E,B(u)≥0.当∥u∥E→∞时, 由文献[1]知Iλ在λ∈[1,2]上是有界集映射到一致有界集. 2.3 引理 引理2.3.1[1,13]在假设的(V1)条件下,E嵌入到Ls(R3),2 引理2.3.2假设(f1)-(f4)成立,则存在ρk>rk>0,使得 证明(i)由(f4)知,对任意的M>0,都存在一个δ>0,使得对所有x∈R3,|u|≥δ有 由(f2)知,存在M1(M1与δ,M有关),对任意x∈R3,α≤|u|≤δ, 通过(3),(4)式,当x∈R3,0≤|u|≤δ时, 而对于u∈Yk,由(f1)知|b(x)| (ii)由文献[1]中的引理3.2可知,Cε>0,存在Cε>0,使得x∈R3,u∈R时, F(x,u)≤ε|u|2+Cε|u|p.令 当k→∞时,βk→0(由文献[15-16]可证)由此当u∈Zk,ε>0且充分小时,结合(V1)有 因此,定理2.2.1,定理2.2.2条件满足,故对任意的λ∈[1,2],存在序列有 故λn→1,λn∈[1,2]时,可以找到一个序列uk(λn)(为简单起见用un代替),并且此序列满足 引理2.3.3在定理1.1的假设条件下,序列{un}是有界的. 证明利用反证的方法进行证明 假设∥un∥E→∞,令由于E嵌入到Lt(R3),2≤t<2∗,因此在E中,wn弱收敛于w,在中,当2≤t<2∗时,wn强收敛于w;对任意的x∈R3,wn(x)强收敛于w(x). 情况1当E中w/=0,由[1]知则 通过整理变形得: 另一方面,在Ω={x∈R3|w(x)/=0} 而由文献[1]知,当|Ω|>0时 与(7)式矛盾. 情况2在E中W=0,如同文献[1,10]中,可定义对任意的M>0,令 因此,由文献[1]知,对任意x∈R3,u∈R,F(x,u)≤ε|u|2+Cε|u|p,有 令n→∞时, 由于b(x)是有界的且大于0的函数,则Iλn(tnun)≥M,故 由(f5)及文献[1]可得 与(8)式矛盾,故命题得证. 结合引理2.3.1,引理2.3.2,引理2.3.3和定理2.2.1,定理2.2.2及文献[1]可知,在E中,当n→∞时,un→uk, 而 而当I∈C′(E)时,在E∗中I′(un)→I′(uk),故可得∀v∈E,都有 从而〈I′(uk),v〉=0,故对任意的v∈E,在E∗中都有I′(uk)=0.由(9)式以及→+∞知是泛函I的临界点的无界序列.故命题得证. [1]Li Qingdong,Su Han,Wei Zhongli.Existence of in fi nitely many large solutions for the nonlinear Schr¨odinger-Maxwell equations[J].Nonlinear Analysis,2010,72,4264-4270. [2]Ambrosetti A,Ruiz D.Multiple bound states for the Schr¨odinger-Poisson problem[J].Commun.Contemp. Math.,2008,10:391-404. [3]Coclite G M.A multiplicity result for the nonlinear Schr¨odinger-Maxwell equations[J].Commun.Appl. Anal.,2003,7:417-423. [4]D′Aprile T.Non-radially symmetric solution of the nonlinear Schr¨odinger equation coupled with Maxwell equations[J].Adv.Nonlinear Stud.,2002,2:177-192. [5]Kikuchi H.On the existence of solution for elliptic system related to the Maxwell-Schr¨odinger equations[J]. Nonlinear Anal.,2007,27:1445-1456. [6]Ruiz D.The schr¨odinger-possion equation under the e ff ect of a nonlinear local term[J].J.Funct.Anal., 2006,237:655-674. [7]Azzollini A,Pomponio A.Ground state solutions for the nonlinear Schr¨odinger-Maxwell equations[J].J. Math.Anal.Appl.,2008,345:90-108. [8]Pietro d′Avenia,Alessio Pomponio,Giusi Vaira.In fi nitely many positive solutions for a Schr¨odinger-Poisson system[J].Nonlinear Analysis,2011,74:5705-5720. [9]Yang Minbo,Zhao Fukun,Ding Yanheng.On the existence of solutions for Schr¨odinger-Maxwell systems in[J].Rocy Mountain Journal of Mathematics,2012,42:1655-1673. [10]Ruiz D.Semiclassical states for coupled Schr¨odinger-Maxwell equations concentration around a sphere[J]. Math.Models Methods Appl.Sci.,2005,15:141-161. [11]Candela A M,Salvatore A.Multiple solitary waves for non-homogeneous Schr¨odinger-Maxwell equations[J]. Mediterr J.Math.,2006,3:483-493. [12]Zou Wenming.Variant fountain theorems and their applications[J].Manuscripta Math.,2001,104:343-358. [13]Bartsch T,Pankov A,Wang Z Q.Nonlinear Schr¨odinger equations with steep potential well[J].Commun. Contemp.Math.,2001,3:549-569. [14]刘炳初.泛函分析[M].2版.北京:科学出版社,2004. [15]Bartsch T,Willem M.On an elliptic equation with concave and convex nonlinearities[J].Proc.Amer. Math.Soc.,1995,123:3555-3561. [16]Willem M.Minimax Theorems[M].Boston:Birkhuser,1996. Existence of in fi nitely many solutions for the nonlinear Schrdinger system Dong Jing,Wei Gongming In this paper,the existence of in fi nitely many solutions for the nonlinear schr¨odinger system is discussed.Under the certain assumptions on V(x),b(x),f(x)the existence of the in fi nitely many solutions for the correlation equations is proved by weakening the fountain theorem conditions and using the variant fountain theorem.It is simpler than the perturbation method. Schr¨odinger system,in fi nitely many solutions,variant fountain theorem O178 A 1008-5513(2014)03-0299-08 10.3969/j.issn.1008-5513.2014.03.012 2014-05-08. 董静(1988-),硕士生,研究方向:偏微分方程. 2010 MSC:35A15,35A01,35Q40,35Q55,35J50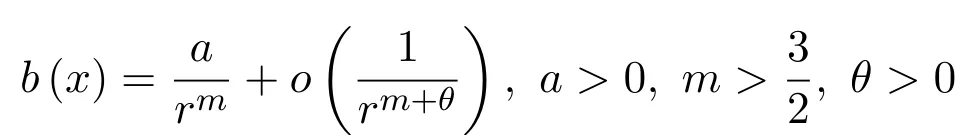



2 相关定理与引理


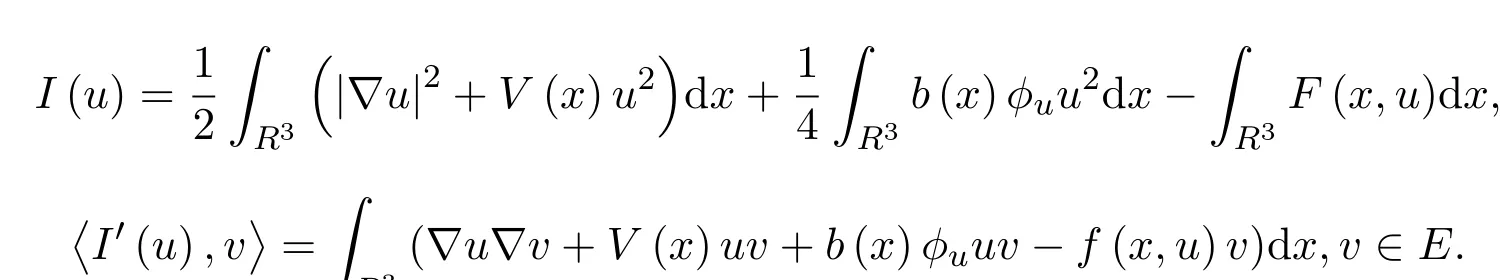
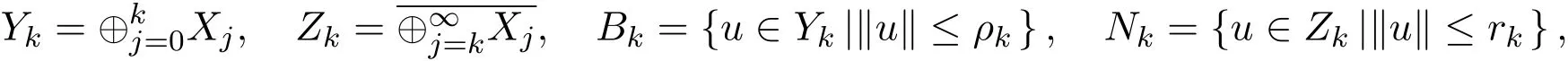





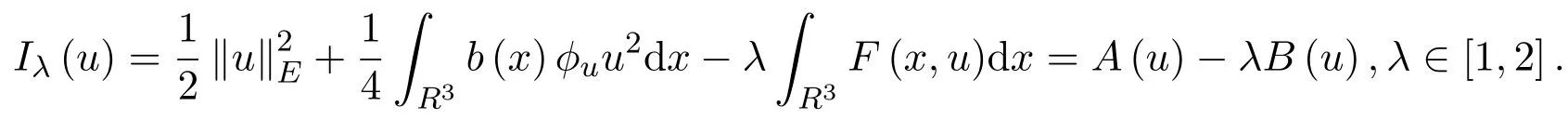


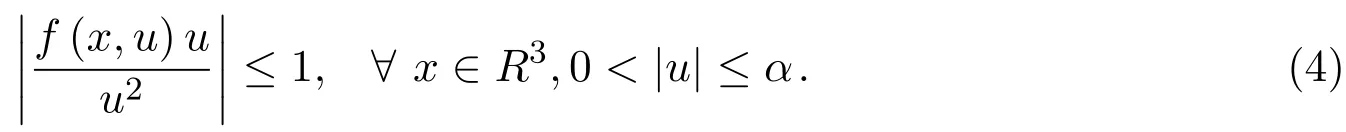

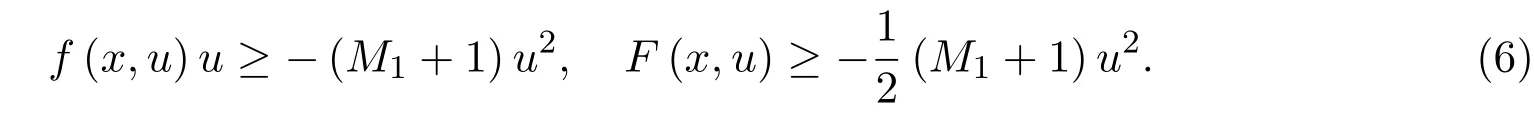

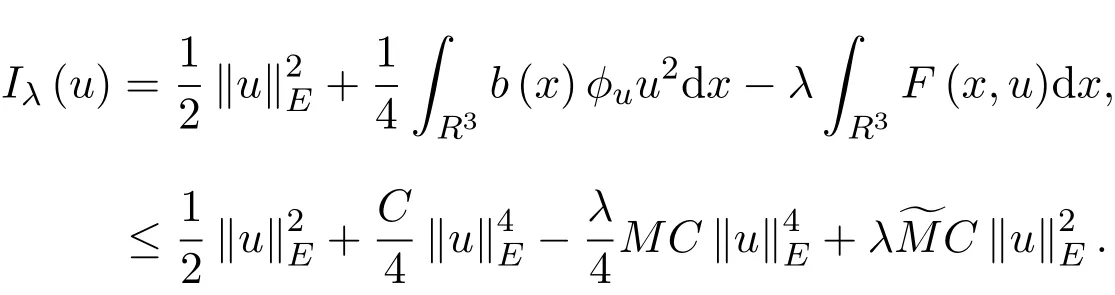




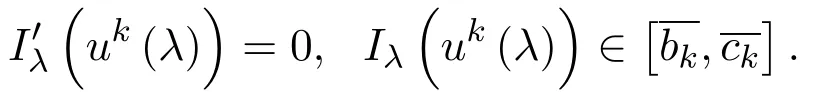


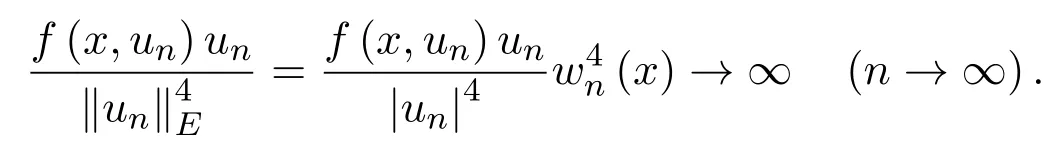
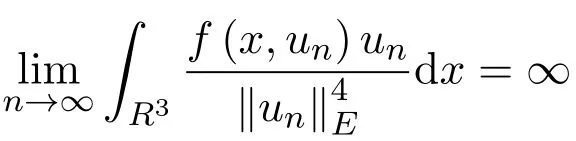
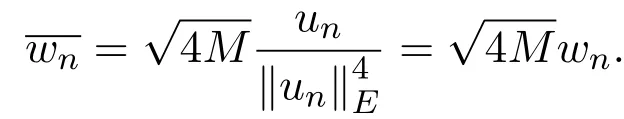

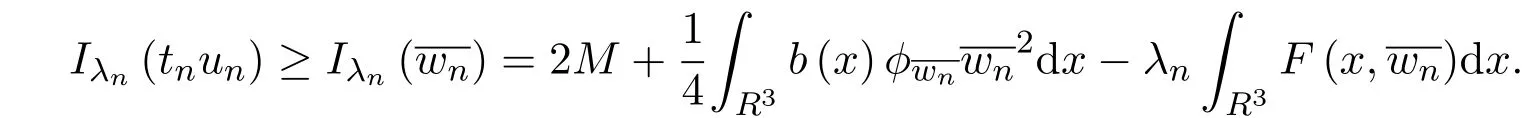

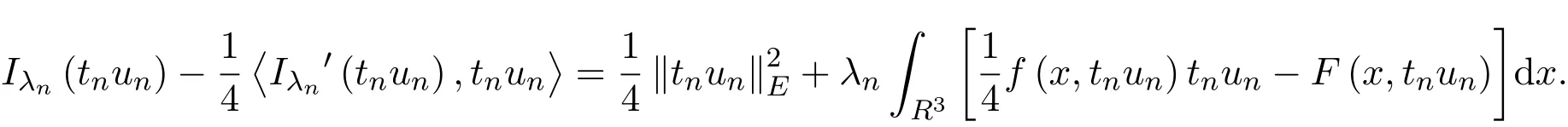
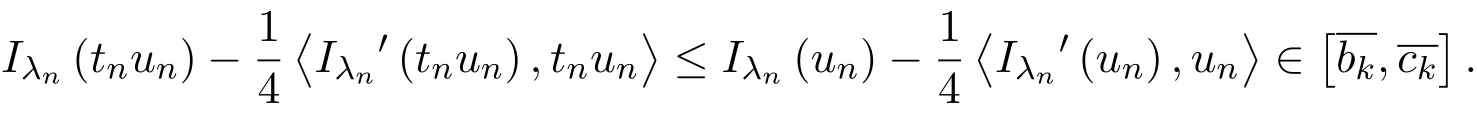
3 定理的证明






(Science School,University of Shanghai for Science and Technology,Shanghai200093,China)

