考虑No-Show的多航段航空机票定价模型

周蔷,刘长有

（1.南京航空航天大学民航学院，南京210016；2.中国民航大学空管学院，天津300300）

考虑No-Show的多航段航空机票定价模型

周蔷1,刘长有*2

（1.南京航空航天大学民航学院，南京210016；2.中国民航大学空管学院，天津300300）

本文提出了多航段航空机票定价模型，从航空公司与旅客两个局中人的博弈的角度，阐述了考虑No-Show下的兼顾多航段航空机票定价模型.该模型由价格控制市场需求出发，结合博弈论、概率论等基本理论，完成多航段机票定价决策的同时，通过价格变化控制机票销量，达到超售有效克服No Show对收益的影响，并同步实现了不同航段舱位的合理分配.算例验证了该模型的可操作性和实用价值.

航空运输；收益；多航段；博弈论；No-Show

1 引言

伴随着航空的迅猛发展和市场竞争的日益加剧，为了合理地优化配置航空运输资源，有关航班在非热点城市实行航班转机运输已成为航空运输与相关组织研究的一大热点，这就形成了多航段舱位控制问题，而核心问题就是在不确定环境下，航空座舱在起飞地和中转地的分配问题.单航段航线只需要考虑一个起飞点的收益与座舱分配问题，而多航段在考虑起飞点的同时，还必须兼顾中转点的顾客及收益问题，因此，承担转机任务的航空公司更应该从收益管理的角度，对起飞点与中转点进行统一考虑，从而实现利润的最大化[1,2].

目前，航空公司收益管理主要是根据旅客的需求，将飞机全部座舱划分为几个等级的子舱，确定各子舱所对应旅客可承受的价格水平，预测出各舱位所对应的旅客需求，然后再确定各舱位的座位数量，使航班的收益最大化.

理论研究方面，早在1972年Littlewood就单航段、两级票价的舱位控制问题提出了边际收益的概念[3].1987年美国的Peter P B在其博士论文中提出了边际期望座位收益方法（EMSR），这种方法已经成为各航空公司舱位控制的经典方法[4].EMSR模型是针对单航段收益最大化的优化模型，并未考虑多航段航线收益最优化.因此，不能用来解决多航段航线收益管理问题.

Wollmer在1986年引入旅客需求的概率性假设的EMR（expected marginal revenue）模型[5]，比较完整地描述了多航段座位控制的实际情况.2005年高强等人根据遗传算法构建了航空收益管理中的多航段舱位控制模型[6].2010年衡红军等人建立了基于椭球体的多航段舱位控制稳健优化模型[7].2012年樊玮等建立了基于分布估计算法的多航段座位分配模型[8].2013年乐美龙等基于风险规避研究了多航段舱位分配问题[9].可见，近年来多航段航空收益管理问题越来越受到业内专家学者的关注，成为该领域研究的重点问题.但大多数研究仅将焦点聚集到航空舱位的控制策略方面，而忽略了航空收益管理的另一重要手段——“超售”.

文献[10]基于博弈论，通过航空公司的机票价格决策调节机票销量，达到控制超售、舱位分配的目的，建立了将机票定价、超售、舱位控制有机结合的收益管理模型.该模型能较好克服No-Show随机性对收益的影响，同步实现定价、超售及舱位控制，有效提高航空公司收益，但目前模型仅适用于单航段情况.本文主要针对这一问题展开研究，解决多航段下定价、超售及舱位的同步控制问题，建立考虑No-Show的多航段航空机票定价模型.

2 基本原理

2.1 航空公司与旅客的博弈

在航空公司与旅客关于机票票价的博弈中，局中人分别为航空公司和旅客.博弈过程中航空公司首先进行决策机票预售价格，然后旅客在获知航空公司决策的条件下根据票价来选择是否购买.因此，该问题是完全信息动态博弈.

定义局中人1为航空公司，局中人2为旅客.航空公司与旅客的动态博弈树形如图1所示.

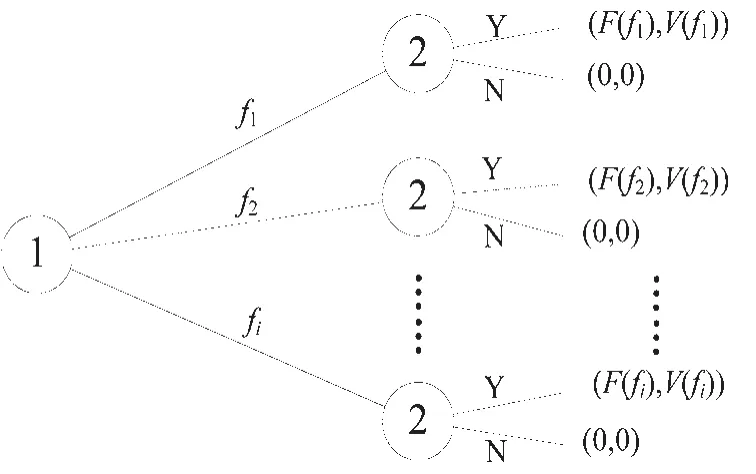
图1 航空公司与旅客的动态博弈Fig 1 Dynamic game of airlines and passengers

图1中fi() i=1,2,…表示航空公司全部航段可行的机票价格方案集，F,V是票价fi的函数，分别表示航空公司、旅客的收益，Y表示“接受”，N表示“拒绝”.

如果旅客选择购买机票，航空公司获得收益F.考虑到旅客具有出行需求，如拒绝购票则只能选择其他出行方式.因此，旅客购票也可获得选择其他出行方式需付出的总成本减去机票价格的收益V.

根据博弈论理论，航空公司与旅客关于机票定价的博弈是非对抗性的合作博弈，局中人共同谋划获得最大利益.因此，航空公司博弈中的理想结局应为

显然，旅客是理性的，会关心自身收益得失.飞机相对于其他传统出行方式而言，在效率、舒适性及心理偏好等方面具有一定优势，只要收益V≥0旅客便会选择接受购票，反之拒绝购票.所以，航空公司可通过适当的机票价格来调整旅客收益V，间接控制旅客决策行为，实现价格、超售及舱位控制的有机结合，获得更高收益.

2.2 旅客收益

若想通过票价调节旅客的收益函数V，进而控制旅客订票数量，首先需了解旅客出行成本.设C为旅客出行总成本，则

将旅客出行总成本分为两部分：

式中Cp视为旅客选择其他出行方式所需支付的票价（如：购买的火车车票价格）；Cs可理解为时间成本，如选择其他出行方式与乘坐航班相比，旅途中所耗时间对旅客造成的损失.

Cp对于所有有出行需求的旅客而言是确定的常数，而Cs却因人而异.如：通常商务旅客的时间观念较强，相对来说时间比较宝贵，所以对他们来说时间成本会更高一些，而时间充足的旅客旅途中所耗时间对他们没有任何影响，时间成本对他们来说几乎为零.社会地位、工作性质、所处环境等不同的旅客对时间认识也不同，导致Cs具有随机性.因此，旅客出行总成本C是随机变量，通常难以确定.

在航空公司定价问题中，某一特定旅客的时间成本具体取值对航空公司制定机票预售价格来说意义并不大.航空公司更关切当选择策略f∗时，有多少旅客会选择接受订票给航空公司带来收益.

根据博弈模型可知，在航空公司做出决策f∗后，收益V≥0的旅客会选择接受订票，即出行总成本满足C≥f∗.反之，旅客将拒绝订票.因此，接受订票的旅客人数可通过C≥f∗的概率表达为

式中 φ为C的分布函数.

显然，φ的建立需要大量统计数据支持，目前还难以准确建立.考虑到分布函数准确与否仅影响到定价策略的准确性，而对定价模型有效性等方面的验证并无影响.因此，文献[10]中利用一个简单假设来验证、分析建立的定价模型，即

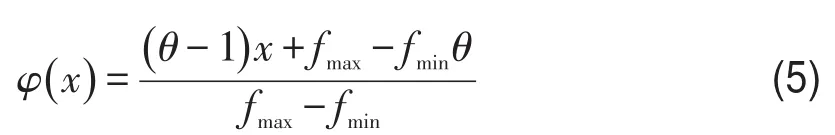
式中fmax为航空公司可选择的机票最高售价；fmin为航空公司可选择的机票最低售价；θ为能够接受价格fmax的旅客占有需求旅客总人数的比例.

3多航段机票定价模型

通过以上分析可知，当预售期一个时间结点上有出行需求旅客人数大于1时，航空公司定价决策对结局影响转化为对接受订票旅客人数的影响.此时，原博弈退化为航空公司的单人博弈问题，航空公司通过价格调控每个时间结点上的订票人数(即不同等级舱位数)，使其利益最大化.

根据机票销售特点，将预售期按天离散，时间结点1≤t≤T表示距航班起飞时刻的天数，向量表示当天各航段有出行需求的旅客人数，

式中 下角标表示航段编号.

则距航班起飞t天订票旅客人数为

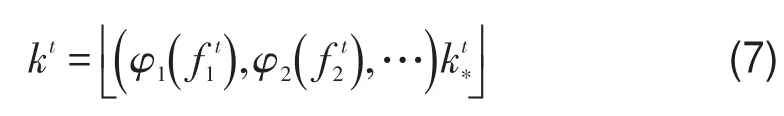
航空公司当天机票销售收益为

式中()T表示对括号内向量的转置运算，下同.

由于各种因素的影响，对于航空公司而言，已经预定机票的旅客在航班起飞时有登机或者No-Show两种可能情况发生.

如果用ktN表示第t天各航段预定机票旅客中发生No-Show情况的人数，且假设No-Show旅客可获得航空公司机票退款fN，则航空公司预售当天机票实际销售收益为

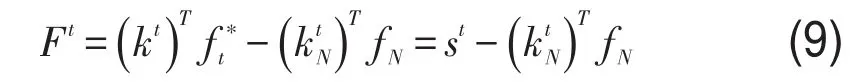
机票预售期内航空公司总销售收益为

如果，航空公司在机票销售过程中充分考虑了旅客No-Show情况，采用超售控制策略，即对应航班的某一航节的机票销售总量超出航班总座位数.那么，航班在该航节起飞时有可能出现三种情况：其一，实际登机旅客人数少于航班座位数，出现空座影响航空公司收益；其二，实际登机旅客人数等于航班座位数，航空公司收益最大；其三，实际到达旅客超出航班总座位数，发生通常所说的

DB情况给航空公司带来经济损失.

将预售期内航空公司总收益看作由销售收益F+和损失F-两部分组成，则

销售收益

损失

式中∑DB为航班在各航节起飞时DB损失之和.若将航空公司损失写为各航节损失和的形式

式中F-j为j各航节起飞时的损失.根据分析可知

式中kNj为航班在j航节起飞时，剩余各航段No-Show旅客人数组成的向量；fNj为剩余各航段No-Show旅客获得退款额组成的向量;c为额定座位数；ηj为判定参数

式中kj为航班在j航节起飞时，剩余各航段购票旅客人数组成的向量；sum()表示对括号内向量全部元素求和.

进而，各航节起飞时的损失函数为

式中fD为每名DB旅客给航空公司造成的损失（包括退票和赔偿）.

所以，航空公司销售机票总收益函数

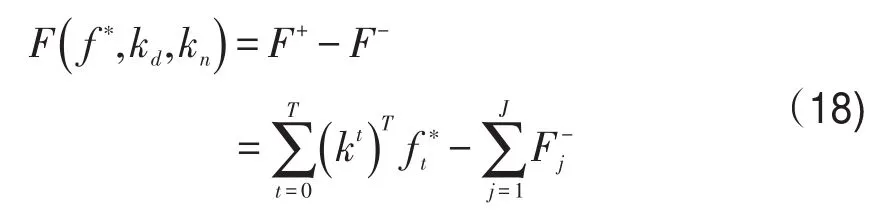
如果考虑有出行需求的旅客人数和旅客No-Show人数的随机性，则总收益期望为

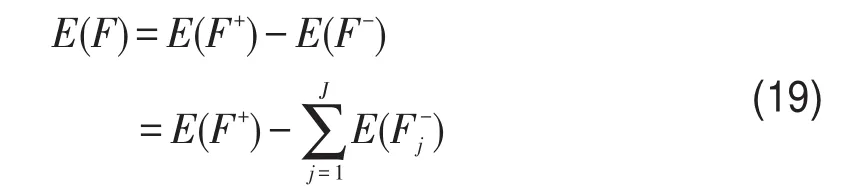
因此，销售期望收益为

由此可见，解决多航段机票定价问题的关键是求解E(Fj-).各航节起飞时的损失函数为分段函数，而其判别参数又为随机变量，如果直接求解模型极为困难.所以，将随机变量ηj的数学期望作为选择该分段函数的依据，简化模型.

各航节起飞时的损失函数改写为

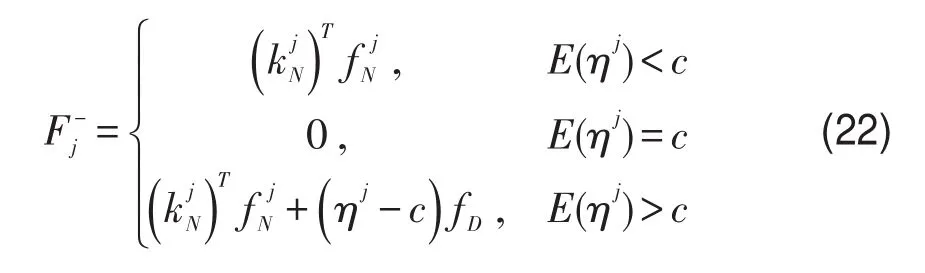
ηj的数学期望为

为便于讨论，对旅客航段进行如表1所示的编码（以三航节航班A→B，B→C，C→D为例）

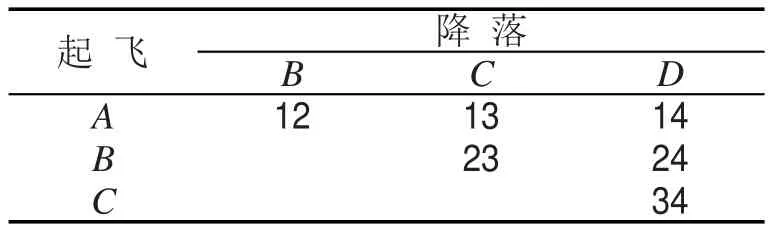
表1 航段编码Table 1 Segment encoding

表1中编码原则为：首先从始发航站开始按飞行顺序依次对各起降点编码.各旅客航段编码第一位数字为始发航站代码，第二位数字为降落航站代码.

采用以上编码原则后，各航段旅客人数表示为如表2所示的代码.

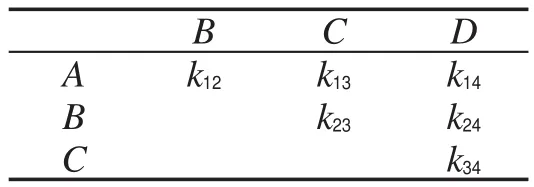
表2 各航段旅客人数Table 2 The number of visitors each leg

对于表2所列情况，航班在第1航节起飞时

进一步分析，航班在第2航节起飞时

若用图示表示其涵盖范围，则如表3虚线箭头圈定部分.

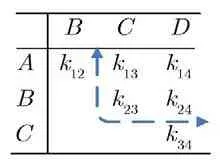
表3 各航节旅客人数范围Table 3 Air passenger numbers for each section range

同理，航班在第3航节起飞时

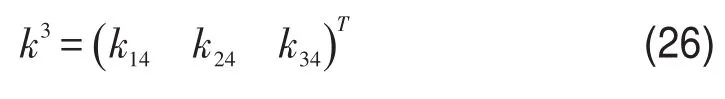
基于以上分析，利用数学归纳法，可得通式

注意到在某航节起飞时，仅有以该行节起飞航站为起点的航段上旅客才有可能发生No-Show情况.同时，考虑到旅客退票与购票时间及持有机票时间的长短无关，即无论旅客何时购票和已购票多久，航班起飞前每名旅客发生No-Show的概率相同.因此，可以将全部预售期内以当前航节起飞航站为起点的各航段所有订票旅客人数作为基数，来研究航班起飞时No-Show旅客的随机性问题.

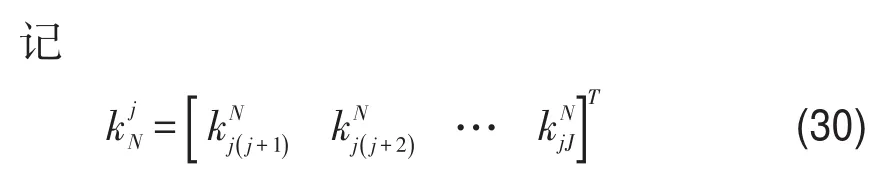
假设每名已经预定机票旅客发生No-Show的概率pN相同，预售期[) 0,t内已订票旅客人数为n时，已订票旅客No-Show的分布律为

若令

代入式（31），即为qm航段全部预售期内已订票旅客发生No-Show情况的分布律.

对该随机变量求期望，得

基于以上推导，预售期内航空公司采用超售控制策略时，各航节起飞时的分段损失函数为

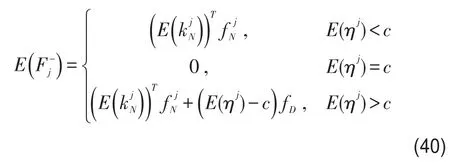
综上所述，即可将多航段机票定价问题描述成以票价ft为基本变量的优化模型.

在实际销售过程中，航空公司对机票预售价格限制为若干种折扣形式，所以动态机票定价模型的优化可行区间属于离散可行域的优化问题.关于离散可行域的优化问题求解方法较多，本文不再复述.

4 算例

某航空公司有一条上海—南京—武汉的两航节三航段航线，按文中所述编码方法对航班起降点编码，上海为1，南京为2，武汉为3，如图2所示.

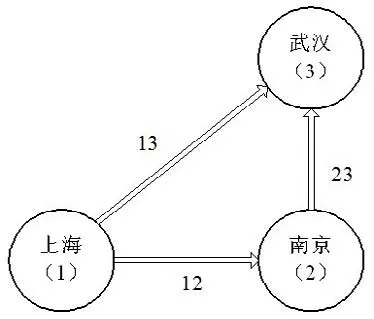
图2 航线示意图Fig.2 Schematic route

执行该航线的飞机有商用座位数为150个.每个舱位在各个航段上的价格集，以及对应的泊松强度如表4所示.

表4 各舱位机票价格与旅客泊松强度Table 4 Ticket prices and passenger space Poisson intensity

根据本算例已知统计数据，文中票价对订票人数的影响，可直接转化为对订票泊松强度的影响，即

因为泊松强度等于每天订票人数的数学期望，所以可通过预售期T的大小来调整订票旅客总人数数学期望，进而模拟航空运输淡季与旺季订票旅客人数的差异，验证方法的可行性.

假设T=20～120天，即旺季客流大约是淡季客流的6倍，利用文中模型对该算例进行定价分析.总收益与T关系如图3所示.

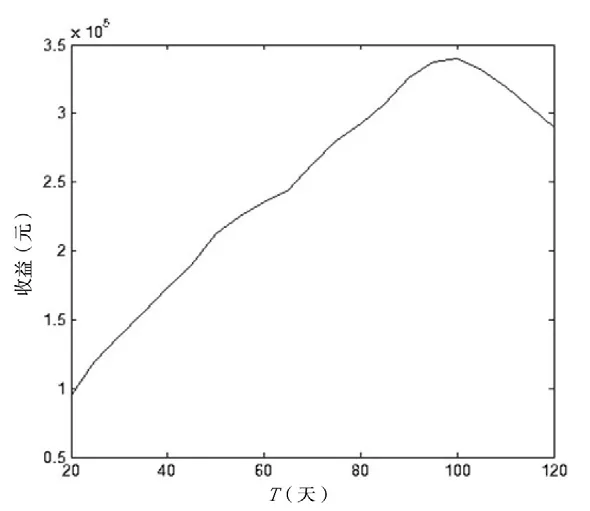
图3 航空公司总收益与T关系Fig.3 Airline total revenue relationship with T

图3中，收益曲线前期随T增加而显著增加，说明本文模型可以较好应对不同的客流情况，给出合理定价策略达到收益最大化.图4也很好的印证了这一点，随着客流量的增大，各航段票价都在升高以达到收益最大.当T大于100天后，由于机票价格已达到允许价格的最大值，客流量却仍然随着T增大不断增加，导致DB可能性快速加大，收益下降，所以图3曲线后期有个明显的快速下降段.这也说明了根据不同客流情况制定合理票价的重要性.

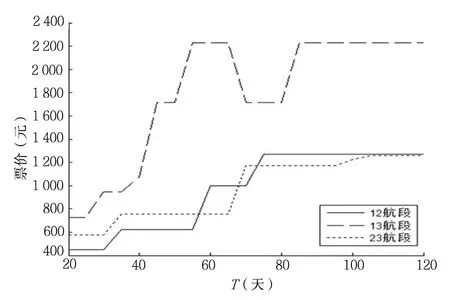
图4 各航段票价与T关系Fig.4 Each leg fare relationship with T

图4中，12、23航段票价稳定上升，而13航段却有个明显的回落段.主要是因为13航段票价相对较高，若发生DB情况航空公司的赔付额越大.所以，在特定客流量组合情况下适当降低其票价，反倒可获得更高收益.

图5 各航段售票数量与T关系Fig.5 The number of tickets for each leg relationship with T

图5中，12航段机票销售数量整体上大于13航段，这样有利于控制票价相对较高的13航段旅客发送DB情况减少航空公司损失.而且通过模型控制，使折扣较大、票价相对较低的12航段具有一定量的销售量.这样有利于出现DB情况时，尽可能将其移至12航段旅客中，有效降低航空公司的经济、声誉损失.

本文模型还成功实现了价格控制的多航段超售，进一步提升了收益.各航节的超售情况如图6所示.

图6中，实线表示该航班额定座位数，可见销量曲线大部分处于该实线之上，说明该模型成功地通过价格控制实现了超售.

图6 超售情况Fig.6 Overbooking situation

T≤25和T≥100时，销量曲线分别远低于和远高于实线，是因为此时机票价格分别达到了可行价格的上下界，模型丧失调控能力.

25≤T≤100时，有部分低于实线情况是因为价格可行集为离散的，出现了选择较高价格减少销量反倒比选择较低价格实现超售获得的收益更高.

5 研究结论

本文建立的多航段机票价格模型，主要基于价格控制市场需求的思路.通过价格调控市场需求，控制机票销量，抑制超售，克服No-Show对航空公司造成的损失，达到收益最大化.

本文模型可以较好地应对航空客流的旺淡季变化，针对不同客流情况制定针对性价格决策，消除No Show影响，控制超售，有效提升航空公司收益.

[1]乐美龙，张健泽.航班超售与舱位控制综合优化[J].河南科技大学学报(自然科学版),2013,03:25-29,108. [LE M L,ZHANG J Z.Overbooking and comprehensive optimization control slot[J].Journal of Henan University of Science&Technology(Natural Science),2013,03:25-29,108.]

[2]彭志强.面向策略性消费者的动态定价及应对机制研究[D].重庆大学,2010.[PENG Z Q.Inter-temporal pric⁃ing and operational mechanisms in the presence of stra⁃tegic consumers[D].Chongqing University,2010.]

[3]Littlewood K.Forecasting and control of passengers[C]. 12th AGIFORS Symposium Proceedings,1972:103-105.

[4]Peter P B.Air travel demand and airline seat inventory management[D].Massachusetts Institute of Technology, 1987.

[5]Wollmer R D.A hub-spoke seat management model[R]. Long Beach,CA,USA:McDonnell Douglas Corporation, 1986.

[6]高强，朱金福，陈可嘉.航空收益管理中的多航段舱位控制模型[J],交通运输工程学报，2005,5(4):82-85. [GAO Q,ZHU J F,CHEN K J.Mul ti-leg seat inventory control model for airline revenue management[J].Jour⁃nal of Traffic and Transportation Engineering，2005,5 (4):82-85.]

[7]衡红军,李雅静.多航段舱位控制稳健优化模型研究[J].计算机工程与设计,2010,12:2887-2889,2893. [HENG H J,LI Y J.Research on robust optimization model of multi-leg capacity inventory control[J].Com⁃puter Engineering and Design,2010,12:2887-2889, 2893.]

[8]樊玮,苏秋波.基于分布估计算法的多航段座位分配模型[J].信息与控制,2012,06:774-778,785.[FAN W, SU Q B.Multi-leg capacity allocation model based on estimation of distribution algorithm[J].Information and Control,2012,06:774-778,785.]

[9]乐美龙,张健泽.基于风险规避的航班舱位分配控制研究[J].广西师范大学学报(自然科学版),2013,02:27-33.[LE M L,ZHANG J Z.Seat Inventory control for flights based on risk-version[J].Journal of Guangxi Nor⁃mal University(Natural Science Edition),2013,02:27-33.]

[10]周蔷,刘长有.基于博弈理论的航空机票动态定价模型[J].江苏大学学报(自然科学版),2013,04:481-485. [ZHOU Q,LIU C Y.Dynamic airline pricing model based on game theory[J].Journal of Jiang su University (Natural Science Edition),2013,04:481-485.]

Air Ticket Pricing Model of Multi-leg Airline Considering No-Show

ZHOU Qiang1,LIU Chang-you2
(1.College of CivilAviation,Nanjing University ofAeronautics andAstronautics,Nanjing 210016,China; 2.ATC College,CivilAviation University of China,Tianjin 300300,China)

ract:Air ticket pricing model of multi-leg airline is put forward,and it is analyzed in detail from the perspective of airline-passengers game,with No-Show considered.Based on the price-controlling market demand and the basic theories including game theory and probability theory,this model defines the multi-leg air ticket pricing decision.In addition,the changing price can control the ticket sales,so that the excessive sales can effectively overcome the impact of No-Show on earnings,and the freight space of different legs can be reasonably distributed.Moreover,case studies are conducted to verify the operability and practical value of this model.

rds:air transport;revenue;multi-leg;game theory;No-Show

1009-6744（2014）04-0201-08

F224

A

2013-12-24

2014-03-26录用日期：2014-04-03

国家自然科学基金重点资助项目（60736045，60472130）.

作者介绍：周蔷(1978-)，男，江苏镇江人，博士生. *

cy_liu511@163.com