基于拉格朗日的高速铁路车站作业优化

白紫熙，周磊山，王劲，郭彬

（北京交通大学交通运输学院，北京100044）

基于拉格朗日的高速铁路车站作业优化

白紫熙，周磊山＊，王劲，郭彬

（北京交通大学交通运输学院，北京100044）

本文从Job-Shop调度角度出发，以列车为待加工的“工件”，将车站接车进路、到发线和发车进路看作“加工机器”，列车在车站的走行与停站看做不同的“作业工序”，把高速铁路车站作业问题抽象成Job-Shop车间调度优化，以设备能力、冲突进路、停站时间为空间和时间约束，以最小化到发线的占用时间为优化目标，建立高速铁路车站作业优化模型.采用拉格朗日方法松弛原模型的约束条件，建立车站技术作业问题的拉格朗日对偶松弛问题，设计了高速铁路车站作业优化模型算法.并以高速铁路的某一车站为实例进行验证，实例表明，该算法可以有效地化解车站作业进路冲突和实现到发线运用时间的最小化.

铁路运输；车站作业优化；Job-Shop；拉格朗日松弛；次梯度算法

1 引言

高速铁路车站作业计划包含接发车作业进路、到发线运用计划、动车组出入段及转线调车作业，也就是为列车安排进路占用方案和到发线运用方案.对车站而言，到发线和咽喉进路属于具有时空约束的固定设备，因此对车站作业进行合理优化具有很重要的意义.在现实行车组织作业中，由于一些不可避免的因素，列车不可能完全按图行车，当列车出现与列车运行图不符时，车站作业的合理安排有利于减小列车的晚点传播的影响.

车站作业问题属于NP-hard问题，在多项式事件范围内很难求到最优解，国内学者大多将车站作业问题抽象成图论问题[1]、0-1规划问题[2]及排序问题[3]，采用分枝定界法[4]或启发式算法求解车站作业问题，主要有蚁群算法、遗传算法、神经网络算法和模拟退火算法等.国外学者的研究比较有代表性的有：Malachy设计了基于冲突检测的股道分配算法，并应用于一系列有多种类型和速度的列车到发的复杂车站[5]；Partha假设列车不一定都能够按照列车运行图的规定时刻到来，建立了混合整数规划来描述车站的进路分配问题[6]；Joaquı´n Rodriguez提出了一个约束规划模型来解决列车在枢纽站的进站路径和时间安排问题[7]；Richard Freling等人提出了一种改进的列生成算法来解决旅客列车进路选择问题[8].

综上，国内外学者的研究大都集中在到发线运用或进路选排两个方面，但是对于高速铁路车站作业的整体综合优化却鲜有研究.本文从Job-Shop调度角度出发，将车站作业问题抽象成“机器、作业与工序”的优化问题，将车站接车（出段）进路、到发线和发车（入段）进路看作机器，列车在车站的走行与停站看做不同的工序，列车作业的彼此与独立之间具有一定的时间和空间限制，在此基础上建模.由于拉格朗日是一种求极值的强有力的经典方法，对于最优化问题有着很好的适用性，在各学科领域都得到了广泛的应用，而在铁路运输组织中却很少涉及，本文采用拉格朗日次梯度算法最终求解模型.

2 高速铁路车站作业计划模型建立

车站作业计划是在时间与空间的双重约束下，为列车安排走行进路与到发线.以列车为准备加工的“工件”，咽喉进路与到发线为“加工机器”，则车站作业计划可以归结为一类特殊的Job-Shop调度问题.图1为列车车站作业的Job-Shop抽象，全站所有的技术作业类型的工序图可划分成若干个作业串联起来的工序图.分析列车在车站的作业流程，可概括为三道作业工序：

（1）列车经由接车进路，准备进入到发线，对于始发列车来说为出段作业；

（2）列车占用到发线，供旅客上下车或其它列车准备工作；

（3）列车转出到发线，进入出站进路，对于终到列车来说为入段作业.

本文假设一旦确定了列车占用的到发线，则其所对应的接车（出段）进路和发车（入段）进路也是固定的.

图1 列车车站作业的Job-Shop抽象Fig.1 Illustration of train operation at a station

2.1 模型基础

（1）列车开行方案已知，每次列车的种类、到发时刻、运行方向为确定值（可通过查定列车运行图获得）.

（2）不同车场的到发线使用方案已知，列车技术作业内容、作业顺序，以及每项作业的最短时间及最长时间为确定值（可通过查定《站细》获得）.

（3）各个进路与到发线之间的关系已知，可以通过查定车站平面图，建立进路与到发线之间的连通关系.

2.2 模型设计

首先根据列车时刻表，将列车i的车站作业形式化为活动时间链对于始发、终到和通过列车只有其唯一对应的作业时间链，需要强调两种特殊情况：

（1）对于转线折返列车，按两个作业活动时间链分别计算；

（2）对于立折列车，可将两个列车合并成一个作业时间链考虑.

2.2.1 参数定义

l——到发线索引；

T(k)——车站k内部的股道集合；

i,j——列车索引，j表示列车i的后续列车；

θi——列车i所占用的到发线的编号；

(i,m)——列车i的第m道工序；

jobi——列车i的车站作业表示列车经由咽喉准备进入到发线，即m=1；表示列车占用到发线作业，即m=2表示列车转出到发线进入咽喉，即m=3；

Si,m——列车i的第m道工序的开始时间；

Ei,m——列车i的第m道工序的结束时间；

Til——列车i占用到发线l的时间；

2.2.2 决策变量

（1）二进制变量.

（2）连续变量. ail——列车i进入到发线l的时间，l∈T(k)；dil——列车i离开到发线l的时间，l∈T(k).

2.2.3 目标函数

最小化列车在车站的停站时间，一般情况下，客运站在满足技术作业要求的前提下应尽快腾空到发线.函数式（1）表示某方案下列车在车站的停站时间总和，函数式（2）为本模型的目标函数，最小化列车在车站的停站时间.

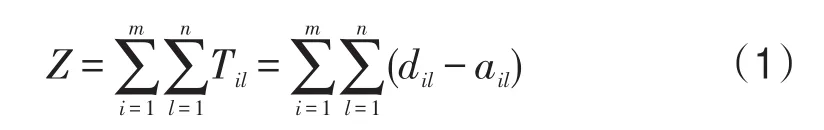
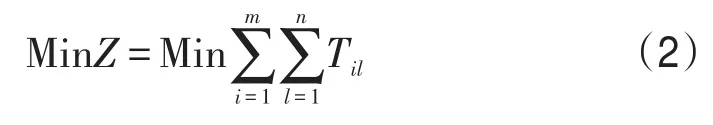
2.2.4 约束条件

安排列车作业时需满足以下约束：

（1）设备能力约束.在t时刻，到发线l只会被一个列车占用，

（2）列车作业分配约束.一列车只能占用一条到发线，

（3）停站时间约束.

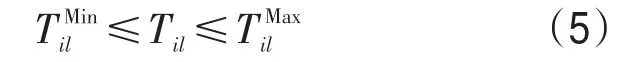
（4）运动的连续性约束.

（5）冲突进路约束.

将车站的拓扑结构用连接车站各方向边界和股道的接发车进路表示.任意两条进路间可能会因为共用一个道岔或轨道单元而存在空间上的重叠，因此对于作业进路上存在交叉干扰的作业，需保证一定的安全间隔时间.h1表示两接车进路的安全间隔时间，h2表示两发车进路的安全间隔时间，h3表示到发进路冲突的间隔时间，h4表示发到进路冲突的安全间隔时间，如图2—图4所示.对于分配在不同到发线的列车i和j，如果作业进路上存在交叉干扰，也必须保有一定的安全间隔时间，这里我们认为列车i比列车j具有优先权.

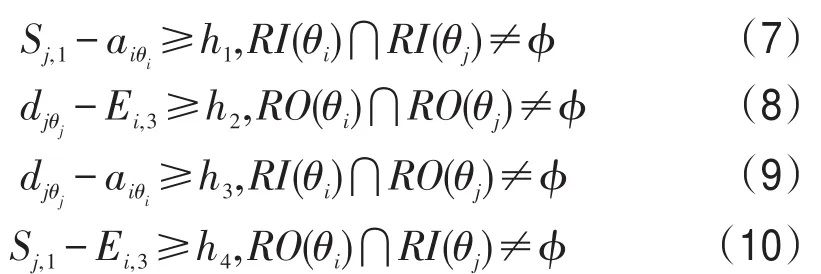
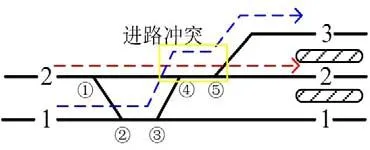
图2 敌对进路Fig.2 The confliction between two receiving routes

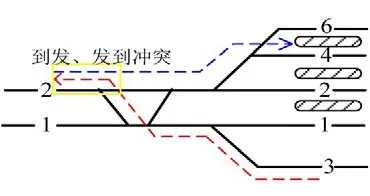
图3 到发、发到进路冲突Fig.3 The confliction between a departure route and a

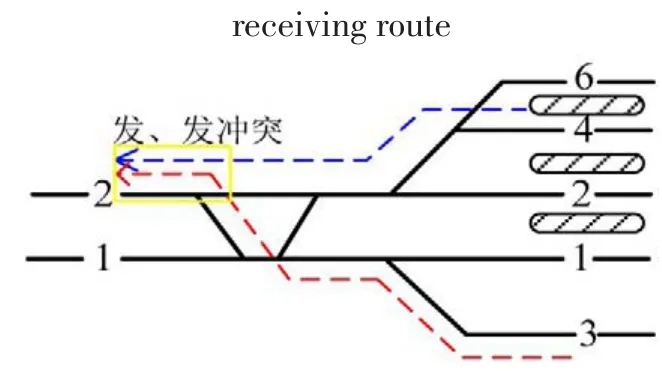
图4 发发进路冲突Fig.4 The confliction between two departure routes

3 基于拉格朗日松弛的车站作业模型

3.1 车站技术作业问题的拉格朗日对偶松弛问题

将约束（3）松弛，则原问题变成了不考虑设备能力约束的简单问题.拉格朗日乘子法是一种求极值的强有力的方法，本文给定一个非负的拉格朗日乘子 λtl，记车站技术作业问题的拉格朗日松弛问题为ZLR，描述如下：

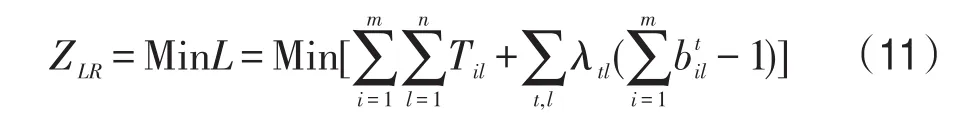
原问题的拉格朗日松弛对偶问题形式如下，记为ZLD：

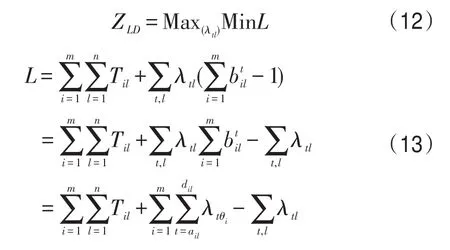
将拉格朗日松弛对偶问题（12）分解为两部分，非正则子问题（14）和正则子问题（15）.当给定一组拉格朗日乘子 λtl时，式（14）为定值.正则子问题可基于不同列车的技术作业进行分解.

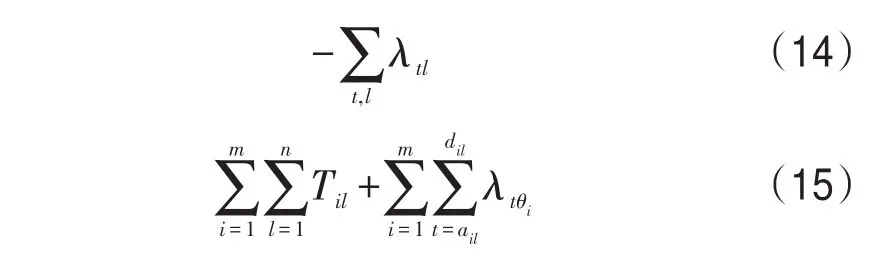
正则子问题可以基于列车分解：

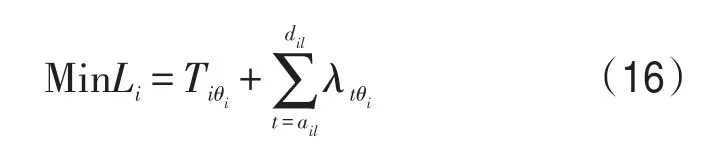
λtl反映了t时刻占用到发线l所需要付出的代价，占用不同的到发线需要付出相应的代价.式（16）的目标是确定列车占用的到发线及其占用时间，使其占用到发线所付出的代价和停站时间的总和达到最小.

3.2 次梯度算法优化拉格朗日乘子

对于拉格朗日求解的算法设计，Kibardin认为部分的最优解与整体的最优解是基本一致的，提出次梯度算法是求解拉格朗日问题的有效方法[9].可以通过子问题的求解过程得到.

式中 拉格朗日乘子 λtl的初始值为0，上标n表示迭代次数.Stl表示拉格朗日乘子 λtl的次梯度方向，如式（18）所示；ηn表示第n次迭代的步长，可以通过式（19）求出，其中Z¯表示原问题的期望值，Z表示第n次迭代的结果，β是步长调节因子.

Stl＞0则说明有多辆列车同时占用同一条到发线，价格上升，下一次迭代的时候便会绕开该冲突.

4 高速铁路车站作业优化算法

step1初始化.

读取t0时刻车站到发线及进路占用数据.构建t×l阶矩阵 λTL和CTL，矩阵 λTL中元素 λtl表示t时刻编号为l股道的拉格朗日乘子值，初始值全部取零.矩阵CTL表示股道被占用的时间信息，其中ctl表示t时刻占用编号为l的股道的列车数量.

step2安排时间窗长度内的列车作业.

定义时间窗长度为K，根据时刻表读取K时间内需要安排到发线的列车的信息，确定列车作业的时间链

step2.1安排通过列车作业.

根据进入车站的先后顺序，为通过列车安排进路，确定通过列车占用股道的时间信息，并更新矩阵CTL.

step2.2安排其他列车作业.

根据列车进出车站的先后顺序及冲突进路约束，搜索列车的所有可行进路，在列车i的所有可行进路链表中，寻找其占用到发线时间Til与拉格朗日乘子值之和的最小值Li，确定列车占用股道

的时间信息，更新矩阵CTL.

step3根据2.2节介绍的次梯度算法更新拉格朗日乘子λtl.

step4判断迭代是否终止.

通常在循环开始时β=2，并在循环过程中逐步减小.在连续20次的迭代过程中，如果解的质量都没有提高，则令βn+1=0.8βn，n=n+1，进入2.2；若连续100次迭代仍未改善，则终止迭代，获得初始解（参数选取参考文献10）.

step5初始解的可行化.

求解Lagrangean对偶问题，通过松弛复杂约束的办法，相当于扩大了原问题的可行域，故所得的解不一定是可行解，是一个好的初始序列.尤其是当能力比较紧的时候，为得到原问题的可行解，这个时候需要对这个不可行解做可行化处理，例如采用顺延冲突任务的方法，此时原问题将转化为一个简单的纯线性规划问题.至此完成了时间窗内所有列车的作业安排，算法结束.

5 实例分析

本文以高速铁路某一车站为例，以下称为A站.安排其8：00-9：00的车站技术作业，本文规定所有列车在A站的作业时间链为

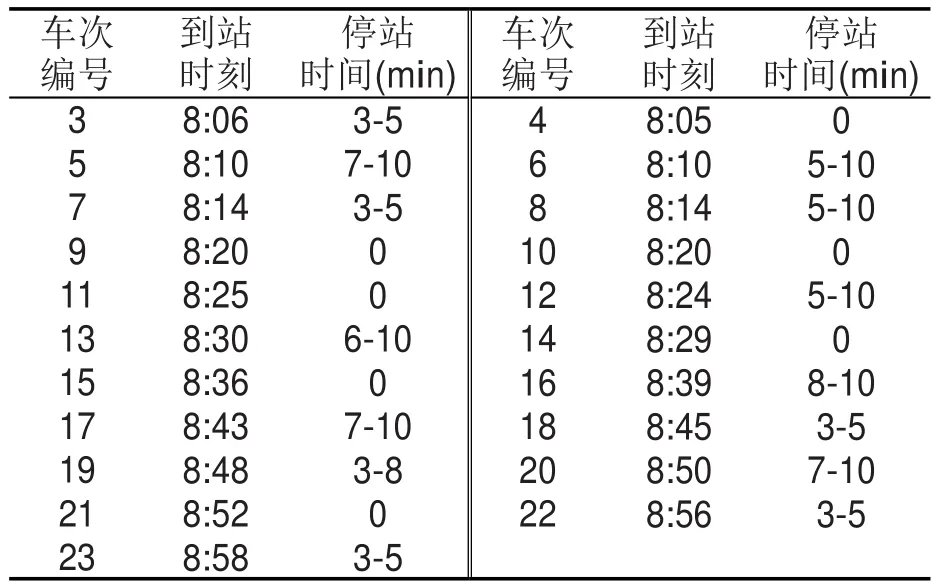
表1 A站8：00-9：00时刻表Table 1 Train schedule of station A during 8 am-9 am

图5 A站站场平面图Fig.5 The planar graph of station A

表2 8:00时分到发线占用表 Table 2 The occupancy on arrival and departure tracks at 8 am

采用matlab进行求解，求解结果如表3-表4所示.其中表3代表下行列车的车站技术作业，表4表示上行列车的车站技术作业.对表1进行分析可知，若列车都以最小停站时间停车，则列车的发车进路会产生冲突，而本文的模型和算法通过延长停站时间，完全疏解了进路在空间上的冲突，说明了本文的模型和算法能有效地避免进路冲突的问题.

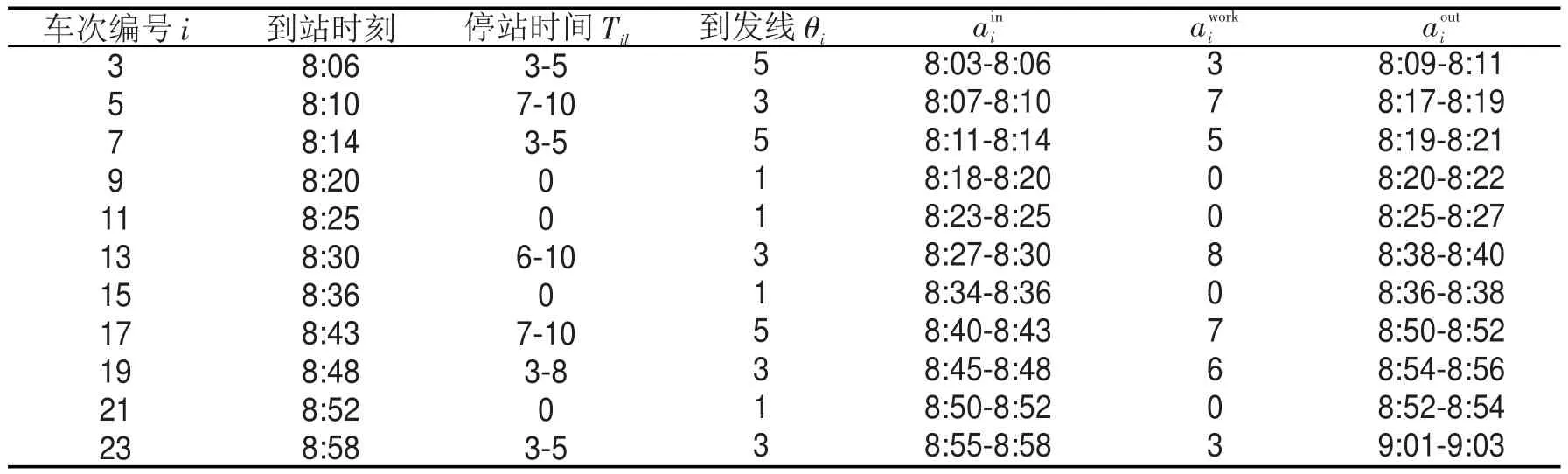
表3 A站8:00—9:00下行列车车站技术作业计划方案Table 3 Station operation plan for down trains during 8 am-9 am

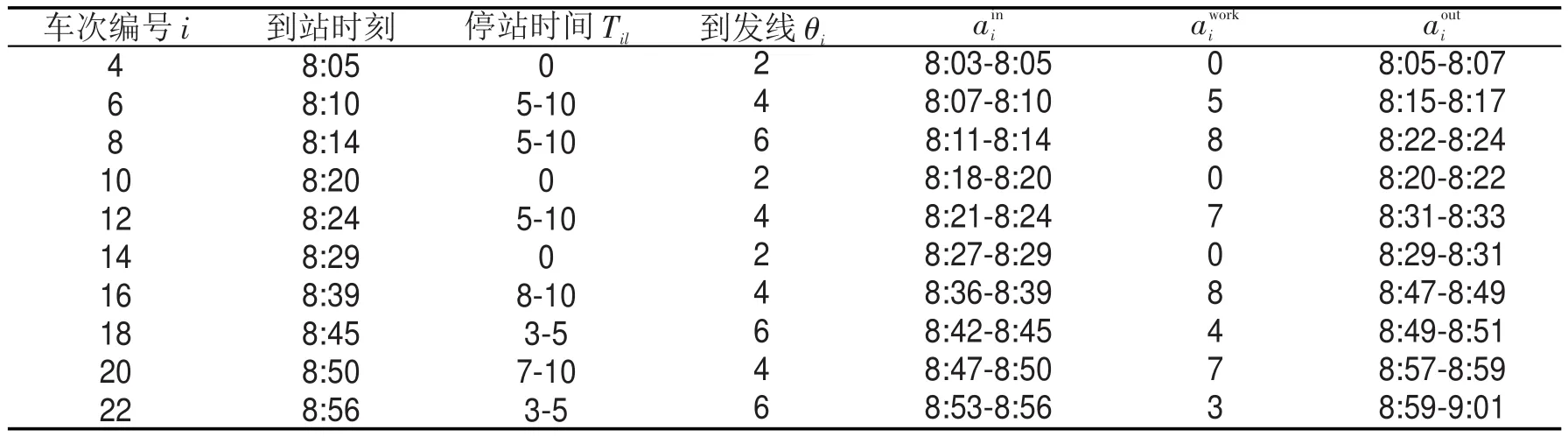
表4 A站8:00—9:00上行列车车站技术作业计划方案Table 4 Station operation plan for up trains during 8 am-9am

6 研究结论

（1）从Job-Shop调度角度出发，以列车为待加工的“工件”，将车站接车进路、到发线和发车进路看作“加工机器”，列车在车站的走行与停站看做不同的“作业工序”，列车作业的彼此与独立之间具有一定的时间和空间限制，将车站作业问题抽象成“机器、作业与工序”的优化问题.

（2）分析了不同种类列车的车站技术作业，以此为基础建立了车站技术作业问题的通用数学模型，采用拉格朗日和次梯度理论简化该通用模型，并设计了车站作业优化模型的求解算法.

（3）以高速铁路的某一车站为实例进行研究，结果表明，本文的模型和算法可以有效地避免进路冲突问题，并可求得到发线占用时间最短的车站作业方案.本文的研究为高速铁路车站作业优化问题提供了一种新的思路和途径.

（4）此外，可将车站作业优化问题作为时刻表优化问题的验算问题，则车站作业计划中关于列车在站停留时间最小可作为反馈，重新优化时刻表，如在车站作业计划优化条件下得到时刻表优化方案则为整体列车运行计划的全局优化方案.如固定列车时刻表，则本文的研究可以用于大站到发线运用和调车作业相结合的车站作业计划优化方法，得到到发线占用时间最小和列车作业干扰最小的作业计划.

[1]徐杰,杜文.基于遗传算法的区段站到发线运用优化安排[J].中国铁道科学,2003,24(2):109-114.[XU J, DU W.The genetic based algorithms optimization plan of using the arrival and departure track at railway sec⁃tional station[J].China Railway Science,2003,24(2): 109-114.]

[2]陈彦,史峰.旅客列车过站径路优化模型与算法[J].中国铁道科学,2010,31(2):101-106.[CHEN Y,SHI F. Optimization model and algorithm for routing passenger trains through a railway station[J].China Railway Sci⁃ence,2010,31(2):101-106.]

[3]张英贵,雷定猷.铁路客运站股道运用窗时排序模型与算法[J].铁道学报,2011,33(1):1-7.[ZHANG Y G, LEI D Y.Due windows scheduling model and algorithm of track utilization in railway passenger stations[J].Jour⁃nal of the China Railway Society,2011,33(1):1-7.]

[4]谢楚农,黎新华.铁路客运站到发线运用优化研究[J].中国铁道科学,2004,25(5):130-133.[XIE C N,LI X H.Optimization research for utilization of arrival and de⁃parture tracks in railroad passenger station[J].China Railway Science,2004,25(5):130-133.]

[5]Malachy Carey,Sinead Carville.Scheduling and plat⁃forming trains at busy complex stations[J].Transportation Research Part A,2003,37：195-224.

[6]Partha Chakroborty,Durgesh Vikram.Optimum assign⁃ment of trains to platforms under partial schedule com⁃pliance[J].Transportation Science,2008,42:169-184.

[7]Joaquı'n Rodriguez.A constraint programming model for real-time trains scheduling at junctions[J].Transporta⁃tion Science 37:213-222.

[8]Richard Freling,Ramon M Lentink,Leo G Kroon,et al. Shunting of passenger train unitsin a railway station[J]. Transportation Science,2005,39(2):261-272.

[9]Kibardin V M.Decomposition into functions in the mini⁃mization problem[J].Automation and Remote Control，1980，40(8)：1311-1323.

[10]Diaby M,Bahl H C,Karwan M H,et a1.A Lagrangean relaxation approach for very-large-scale capacitated lot-sizing[J].Management Science,1992，38(2):1329-1340.

A Lagrangian Relaxation Model for High-speed Railway Station Operation Optimization

BAI Zi-xi,ZHOU Lei-shan,WANG Jin,GUO Bin
(School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

ract:This paper applies the Job-Shop scheduling theory to station operation optimization of highspeed railway.In this study,trains are regarded as workpieces,the arrival-departure tracks,inbound and outbound road are regarded as machines,trains’operations at a station are treated as different works.In this way,the station operation optimization problem can be transformed into a special kind of job-shop problem. The study takes the station equipment capacity,conflicts in inbound road and outbound road,station dwell time as the space and time constraints.The optimization goal is to minimize dwell time of trains.,Then,the paper develops the high-speed railway station operation optimization model and the corresponding Lagrangian relaxation model of station operation.The optimization algorithm is also proposed for high-speed railway station technique operation.A real high-speed railway station case shows that the model and algorithm are able to generate the optimization plan for high-speed railway station operation and they can effectively eliminate the conflicts in inbound road and outbound road.

railway transportation;station operation optimization;Job-Shop;lagrangian relaxation;subgradient

1009-6744（2014）04-0120-06

U292.1

A

2013-11-25

2014-03-11录用日期：2014-03-18

国家科技支撑计划(2009BAG12A10-7)；铁道部科技司项目（2012X011-C）；中央高校基本科研业务费专项资金资助（2013YJS046）.

白紫熙（1988-），女，山西晋城人，博士生. *

lshzhou@bjtu.edu.cn