基于广义巢式Logit的多用户多准则随机用户平衡模型
李雪飞,郎茂祥
(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)
基于广义巢式Logit的多用户多准则随机用户平衡模型
李雪飞,郎茂祥*
(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)
介绍了广义巢式Logit的基本理论,在此基础上,考虑具有不同时间价值的多种用户类别出行者,构造了基于广义巢式Logit的多用户多准则随机用户平衡的等价数学规划模型,并对该模型的等价性和唯一性进行了证明.设计了求解所提出的随机用户平衡模型的基于路径的相继平均法,通过一个算例验证了所设计算法的有效性.分析了分散系数变化对交通分配结果的影响,最后与多项式Logit的分配结果进行对比.算例结果表明,本文所提出的模型能够克服多项式Logit模型的IIA特性,设计的算法具有较高的求解效率.
城市交通;随机用户平衡;相继平均法;广义巢式Logit;多用户;多准则
1 引言
交通分配模型研究是交通规划领域研究的热点问题.自从Daganzo和Sheffi[1]在1977年提出随机用户平衡(Stochastic User Equilibrium,SUE)配流原则以来,众多学者构建和发展了多种随机用户平衡模型.Fisk[2]构建了随机用户平衡的数学规划模型,该模型的解对应于Logit路径选择公式. Sheffi和Powell[3]构建了随机用户平衡的无约束数学规划模型.周晶和徐晏[4]考虑出行需求随节点间拥挤程度的变化,构建了基于弹性需求的随机用户平衡分配模型.刘海旭和蒲云[5]定义了行程质量的概念,构建了基于行程质量的随机用户平衡分配模型.张波等[6]给出了交通流连续分布下路径前景的连续函数表达式,构建了基于累积前景理论的随机用户平衡分配模型.余孝军等[7]构建了基于Logit模型的、具有固定需求的多用户类随机均衡的变分不等式模型,并研究了在时间和费用度量两种出行准则下的效率损失上界.徐兵和朱道立[8]研究了非对称费用函数、多用户类、多准则、固定需求下的随机用户平衡模型和算法.
路径选择模型是随机用户平衡分配模型的核心.通过总结可以发现,目前大部分研究中所采用的路径选择模型是多项式Logit(MNL)模型.然而,由于多项式Logit模型具有不相关备选方案的独立性(IIA)[9]等不良特性,无法反映路径重叠对用户路径选择行为的影响.同时,以往很多研究中假定路网中所有的使用者性质相同,然而当使用者面临出行时间和货币成本等多个准则时,由于收入水平和个人偏好等因素的影响,会造成用户的路径选择不同.因而有必要根据用户的性质进行分类,建立具有多用户多准则的随机用户平衡分配模型,使交通分配结果与实际情况更加接近.
基于以上分析,本文采用Chieh-Hua Wen和Frank S Koppelman[10]所提出的可以克服MNL模型IIA特性的广义巢式Logit模型,并对路网使用者进行分类,建立基于广义巢式Logit的多用户多准则随机用户平衡模型(MMSUE-GNL).对所构建模型的等价性和唯一性进行证明,并设计求解该模型的基于路径的相继平均法(MSA).最后通过一个算例验证了所提出算法的有效性,分析参数变化对交通分配结果的影响,并与多项式Logit模型的分配结果进行对比分析.
2 基于广义巢式Logit的多用户多准则随机用户平衡模型构建
2.1 广义巢式Logit模型的基本理论
McFadden[11]提出了广义极值(Generalized Extreme Value,GEV)理论,该理论为路径选择模型的发展提供了更加广阔的空间,先后有多种新的路径选择模型被提出和应用.广义巢式Logit[10](Generalized Nested Logit,GNL)模型作为GEV模型的一种,具有捕获方案之间相似性的特点,能够克服MNL模型的IIA特性.
本文采用一个双层巢式结构来进行研究,上层为交通网络中的所有路段(巢),下层为OD间所有有效路径.每一条路径可以属于不同的巢,并以分配系数表示一条路径属于某一个巢的比率.广义巢式Logit模型中OD对rs间第i类用户选择路径k的概率为[10]
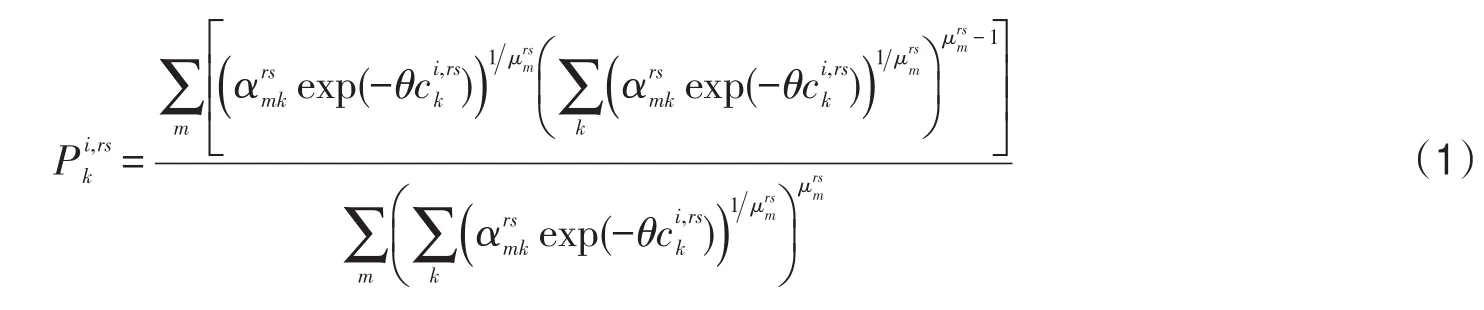
广义巢式Logit模型的概率表达式可以分解为包含边际概率和条件概率的公式:
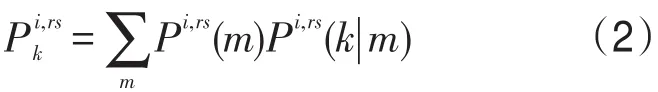
上式中,OD对rs间第i类用户选择巢m的边际概率为
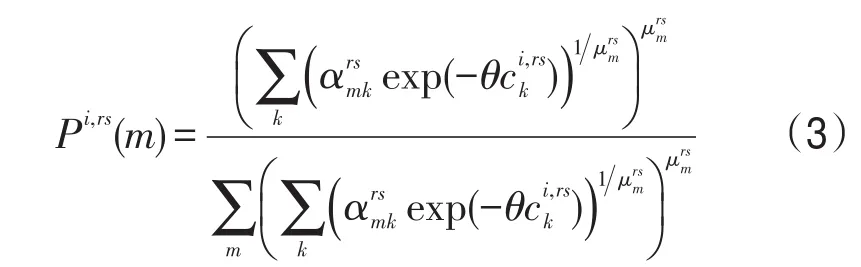
在选择巢m的条件下选择第k条路径的条件概率为
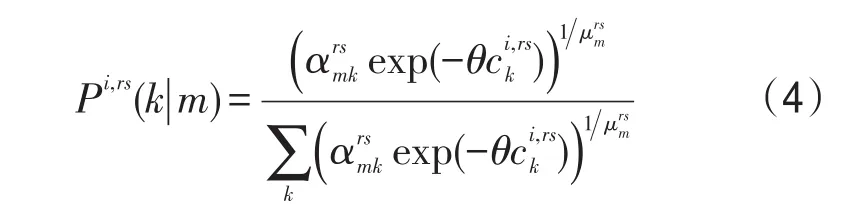
2.2 模型的构建
考虑用一个赋权有向图G(N,A)来表示交通网络,其中N为网络中所有节点的集合,A为所有边(路段)的集合.R为所有OD对的集合,rs表示以r为起点,s为终点的一个OD对,rs∈R.K为所有OD对间路径的集合,Krs为OD对rs之间的有效路径集合,Krs∈K,k为OD对rs之间的第k条路径,k∈Krs.M为巢的集合,m∈M.xia表示路段a的第i类用户的流量,xa表示路段a的总流量.qirs为OD对rs间第i类用户的出行需求量,本文设定为固定值.fmi,krs为OD对rs间第i类用户属于第m个巢的路径k的流量.
本文根据用户所具有时间价值的不同将用户分为I类,i为第i类用户,i∈I.本文中广义成本是以时间度量的,第i类用户的广义路段出行时间为
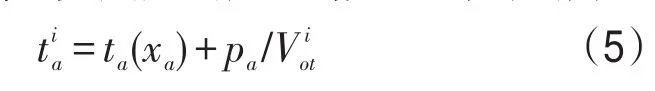
因而rs间第i类用户的广义路径出行时间为
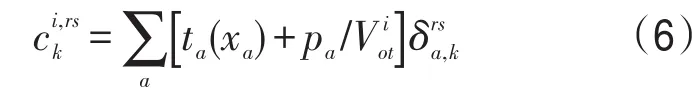
式中ta(xa)表示路段a的出行时间函数;pa为路段a的出行货币费用;Viot为第i类用户的出行时间价值表示OD对rs间若路段a在路径k上,则,否则
本文构建基于广义巢式Logit的多用户多准则随机用户平衡的数学规划模型如下:
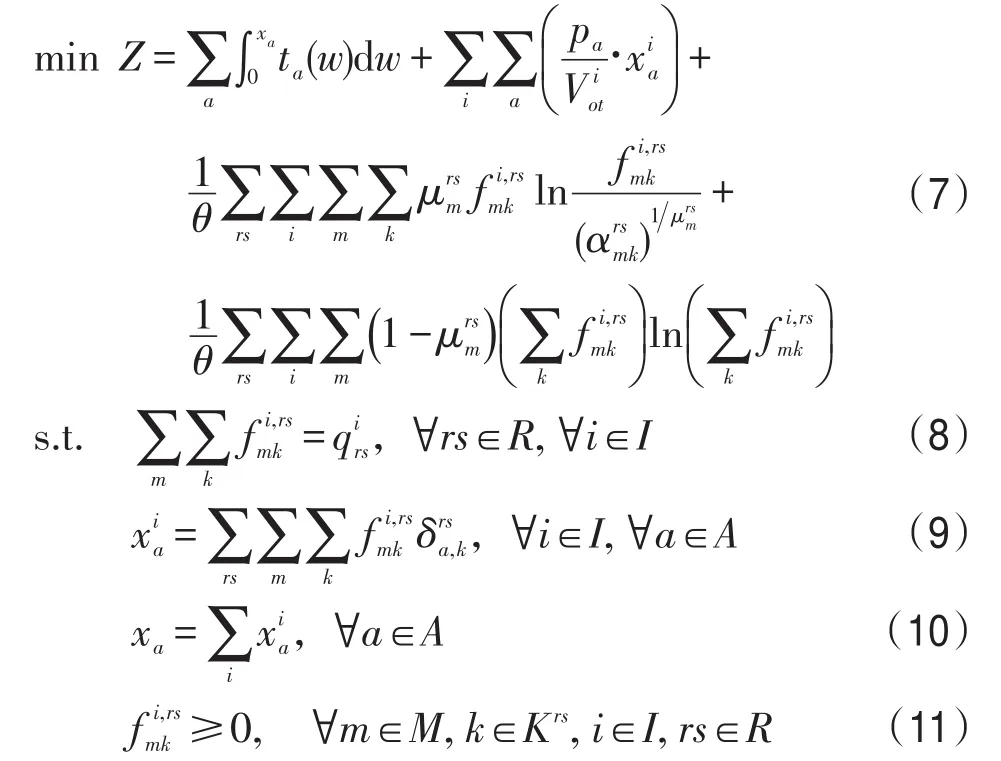
式(7)为最小化目标函数,该式无任何直观的经济意义;式(8)为路径流量与OD量之间的关系;式(9)为分用户类路段流量与路径流量之间的关系;式(10)为路段总流量与分用户类路段流量之间的关系;式(11)是路径流量的非负约束.
定理1本文提出的数学规划模型与基于广义巢式Logit的多用户多准则随机用户平衡配流等价.
证明:
首先,构造式(7)的拉格朗日函数:
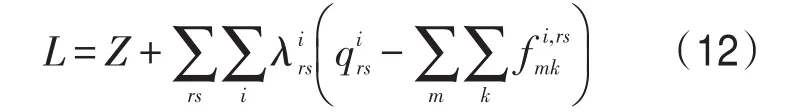
式中λirs为拉格朗日乘子.
对式(12)求导,得到其相应的Kuhn-Tucker条件如下:
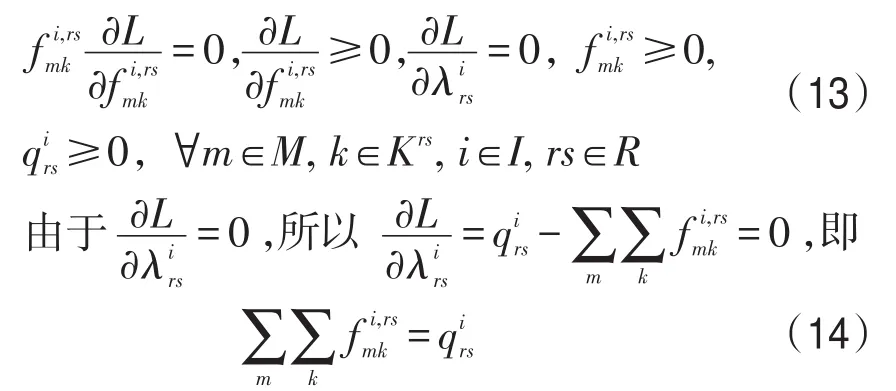
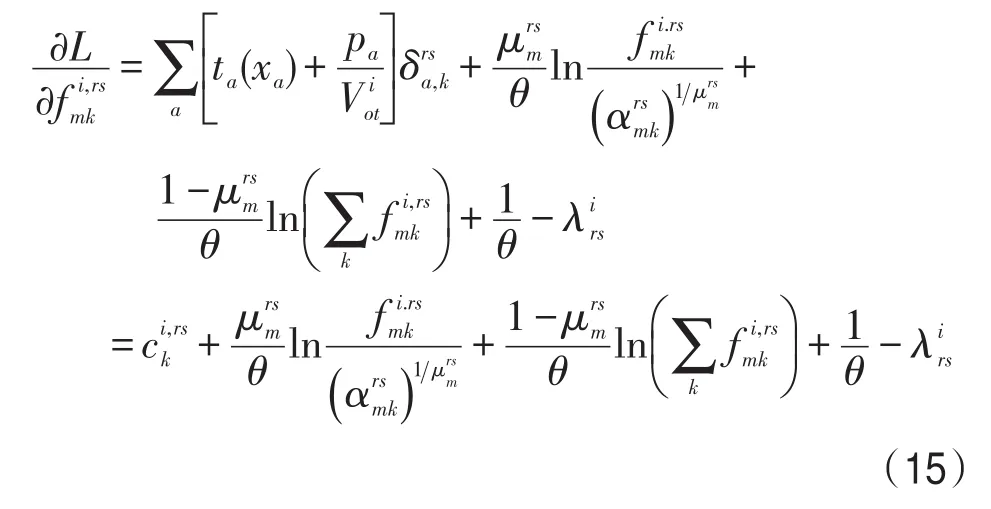

将式(18)对路径k求和,可以得到
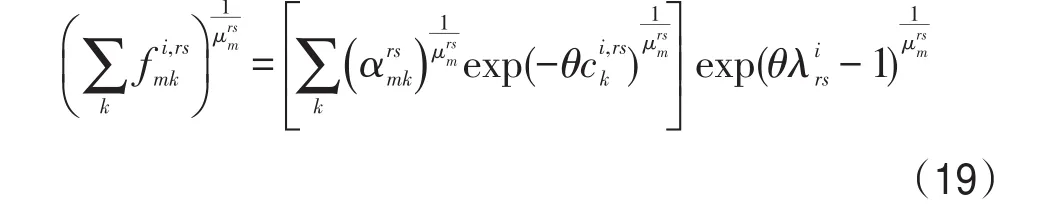
对式(19)取μrsm次方可得
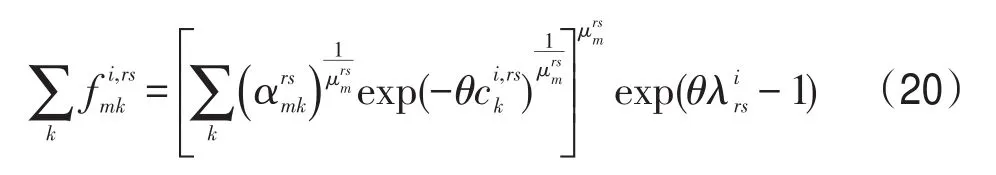
将式(20)对巢m求和可得
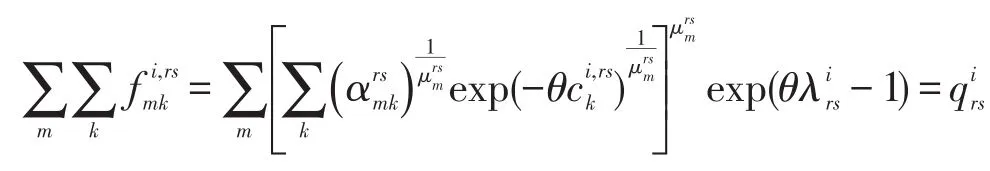
(21)
将式(20)除以式(21),我们可以得到OD对rs间第i类用户选择巢m的边际概率为
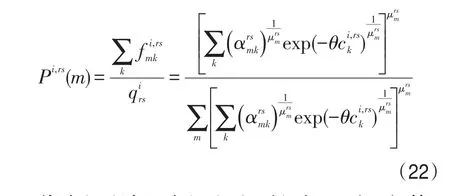
将式(18)除以式(19)可以得到OD对rs间第i类用户选择巢m的条件下,选择路径k的条件概率为
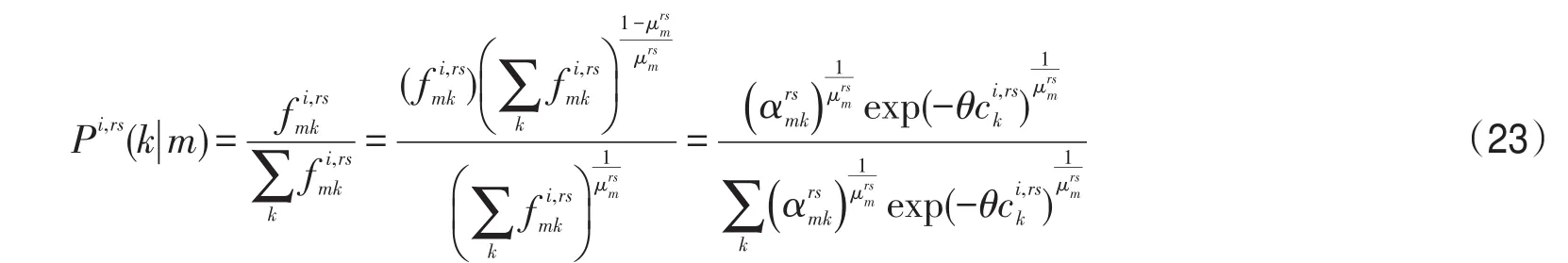
上述式(22)对应于广义巢式Logit的边际概率式(3),式(23)对应于广义巢式Logit的条件概率式(4).
通过以上证明,可以说明本文所提出的数学规划模型与基于广义巢式Logit的多用户多准则随机用户平衡配流等价.
定理2本文提出的数学规划模型的解是唯一的.
证明:
目标函数式(7)的前两项与Yang H和Huang H J[13]所提出的数学规划模型一样,对于路径流量为凸函数,但不是严格凸函数.只需要证明目标函数式(7)的后两项为严格凸的,则可以证明本文所提出的数学规划模型解的唯一性.令目标函数式(7)的第三项和第四项分别为
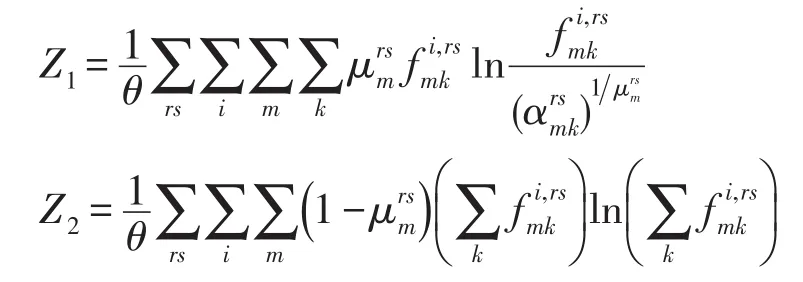
Z1和Z2对OD对rs间第i类用户属于巢m的第k条路径流量fi.rsmk的一阶导数分别为
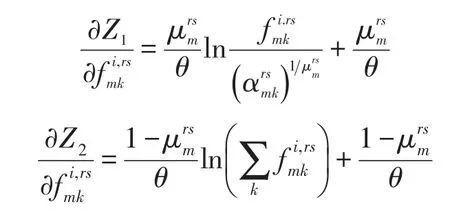
从而Z1和Z2对OD对rs间第i类用户属于巢m的第l条路径流量fi.rsml的二阶导数分别为
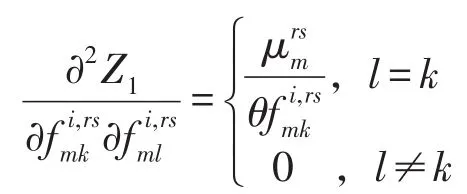
可以看出Z1的二阶导数所对应的Hessian矩阵正定,因而Z1为严格凸函数.
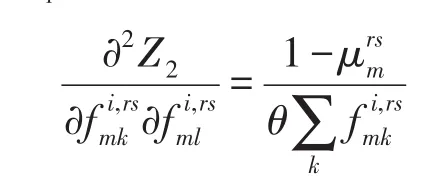
可以看出Z2的二阶导数所对应的Hessian矩阵的每一个元素都相等,因而该Hessian矩阵半正定,因此Z2为凸函数,但不是严格凸函数.
综上所述,目标函数Z是两个凸函数和一个严格凸函数之和,因而Z对于分用户类路径流量为严格凸的.同时,约束条件式(8)-式(11)为非负的线性约束.因此本文所构建的基于广义巢式Logit的多用户多准则随机用户平衡数学规划模型的解是唯一的.
2.3 求解算法设计
本文采用基于路径的相继平均法(Method of Successive Average,MSA)[14]来求解基于广义巢式Logit的多用户多准则随机用户平衡模型.该算法的主要步骤如下:
第1步确定有效路径集合Krs,∀rs∈R.
第2步初始化.根据各路段初始流量为0,各路段的出行货币费用pa及第i类用户的出行时间价值Voit,计算分用户类各路段广义自由出行时间从而计算有效路径的分用户类广义出行时间(∀k∈Krs,i∈I,rs∈R).根据式(1)和计算初始路径流量fki,rs(n),从而获得初始路段流令迭代次数n=1.
第3步更新令tia(n)=ta(x(an))+pa/Voit(∀a∈A,i∈I).
第4步确定下降方向.在当前分用户类路段出行时间tia(n)的基础上,计算新的有效路径的分用户类广义出行时间根据式(1)和可以得到分用户类附加路径流量
第6步收敛性检验.本文采用均方根误差(Root Mean Squared Error,RMSE)来进行收敛判断:
式中K为所有OD对间路径的集合;I为用户类别数;本文取RMSE(n)≤0.0001.当满足精度条件时,算法停止;否则,令n=n+1,返回到第3步继续计算.
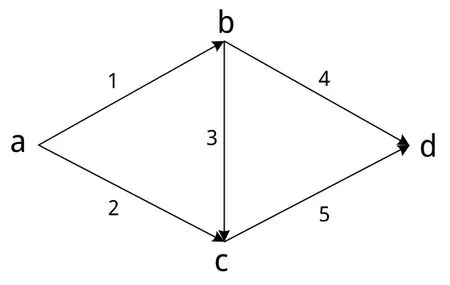
图1 算例网络Fig.1 Example traffic network
3 算例分析
本算例采用如图1所示的交通网络.该交通网络包括3条可选路径,路径1包含路段1和路段4,路径2包含路段1、路段3和路段5,路径3包含路段2和路段5.假设图中的各条路段长度都相等,均为l.算例在具有1.66GHz的Intel T2300处理器的笔记本电脑运行.
假设只有1个OD对ad,总需求量为1000 veh/h.假设路网中有2类用户,即I=2,其中第一类用户的需求为300 veh/h,第二类用户的需求为700 veh/h.路段a的出行时间函数ta(xa)采用广泛使用的BPR函数,即
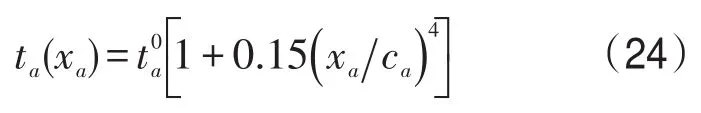
式中t0a为路段a的自由出行时间;xa为路段a的流量;ca为路段a的最大通行能力.
因此,第i类用户的广义路段出行时间为
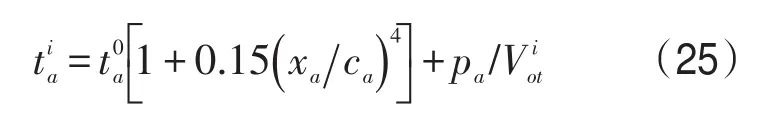
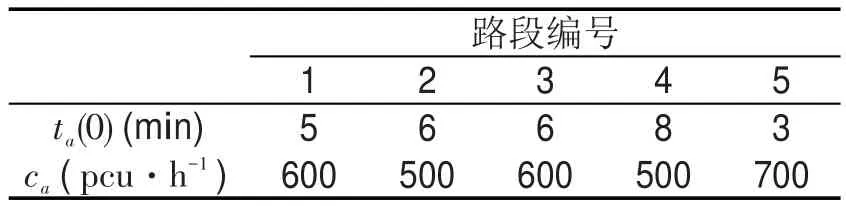
表1 路段自由出行时间及最大通行能力Table 1 The freedom travel time and maximum capacities of different links
算例网络的双层巢式结构、分配系数,以及嵌套系数如图2所示.由图2可知,巢数m=5,路径数k=3.根据式可以得到分配系数根据式可以得到嵌套系数表2给出了当分散系数θ取不同的值时,各路段的平衡流量.
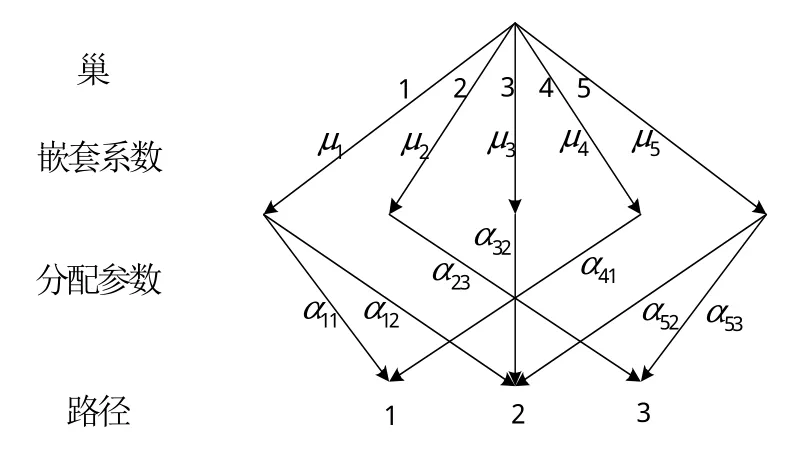
图2 算例网络的双层巢式结构Fig.2 The two-level nesting structure of example traffic network

表2 当θ取不同值时,各路段的平衡流量Table 2 Whenθtakes different values,the equilibrium flow on each link
由表2可以看出,随着θ取不同的值,各路段流量发生了显著的变化.随着θ值的增大,路段1、3和4的流量不断减少,而路段2和5的流量不断增加.当分散系数θ较小时,各条路段都有一定的流量,而当θ增大时,大部分用户选择了路径3.这是由于分散系数θ反映了用户对路况的熟悉程度,θ越大表明用户掌握更多的路网信息,对路况的理解误差较小,因而用户对路径的选择更接近于确定性选择.

图3 当θ取不同值时,算法收敛所需迭代次数Fig.3 Whenθtakes different values,the convergence number of iterations
图3反映了随着θ取不同的值,本文所设计的算法收敛所需要的迭代次数变化情况.
由图3可以看出,本文所设计算法收敛所需要的迭代次数随分散系数θ的增大呈现先增加后减少的趋势.通过求解结果还可以发现,在不同分散系数θ取值下,基于路径的相继平均法能够在7.0秒内达到精度RMSE(n)≤0.0001的要求,具有较高的求解效率.
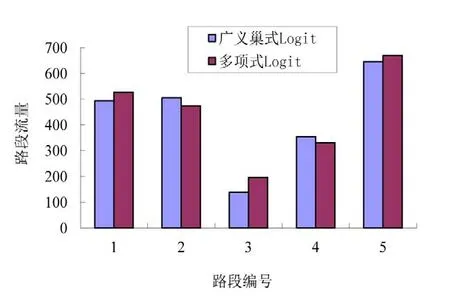
图4 当θ=0.1时,广义巢式Logit和MNL模型分配的路段流量Fig.4 Whenθ=0.1,the link flows assigned by GNL and MNL models
图4对比分析了当分散系数θ=0.1时,分别采用GNL和MNL模型时的路段流量分配结果.可以看出,GNL模型在路段1、3、5分配的流量比MNL模型小,而在路段2和4分配的流量比MNL模型大.MNL模型的IIA特性是由于不考虑路径之间的相关关系而带来的,因而会高估重叠路段的流量,而GNL模型考虑了路径之间的重叠关系,多条路径重合的路段分配的流量要比MNL模型小,能够在一定程度上克服MNL模型的IIA特性,本文的路段分配结果正体现了这一点.
4 研究结论
本文提出了应用广义巢式Logit模型,以及对路网中的用户按照时间价值不同进行分类而构建模型的研究思路.介绍了广义巢式Logit模型的基本理论.构建了基于广义巢式Logit的多用户多准则随机用户平衡数学规划模型,证明了该模型的等价性与唯一性.该模型能够解决路径重叠问题、反映出用户的多类别特点,能够更客观反映实际情况.设计了所构建模型的基于路径的相继平均算法,通过一个算例验证了算法的有效性.分析了参数变化对交通分配结果的影响,并与多项式Logit模型的交通分配结果进行对比.通过算例结果可以看出:分散系数θ对交通分配结果有重要影响,随着θ的增大,交通分配结果不断接近确定性分配;在不同分散系数取值下,本文所提出的算法都能够在较短时间内达到精度的要求;广义巢式Logit模型能够克服多项式Logit的IIA特性,使流量分配结果接近实际.进一步的研究可以考虑将本文提出的模型应用于大型交通网络进行测试,并通过实际数据对模型参数进行标定,研究更加有效的求解算法.
[1]Daganzo C F,Sheffi Y.On stochastic models of traffic as⁃signment[J].Transportation Science,1977,11(3):253-274.
[2]Fisk C.Some developments in equilibrium traffic assign⁃ment[J].Transportation Research Part B,1980,14(3): 243-255.
[3]Sheffi Y,Powell W B.An algorithm for the equilibrium assignment problem with random link times[J].Net⁃works,1982,12(2):191-207.
[4]周晶,徐晏.弹性需求随机用户平衡分配模型及其应用[J].系统工程学报,2001,16(2):88-94.[ZHOU J,XU Y.Stochastic user equilibrium assignment with elastic demand and its application[J].Journal of Systems Engi⁃neering,2001,16(2):88-94.]
[5]刘海旭,蒲云.基于行程质量的随机用户平衡分配模型[J].中国公路学报,2004,17(4):93-95,118.[LIU H X,PU Y.Stochastic user equilibrium assignment model based on travel trait[J].China Journal of Highway and Transport,2004,17(4):93-95,118.]
[6]张波,隽志才,林徐勋.基于累积前景理论的随机用户均衡交通分配模型[J].西南交通大学学报,2011,46 (5):868-874.[ZHANG B,JUAN Z C,LIN X X.Stochas⁃tic user equilibrium model based on cumulative pros⁃pect theory[J].Journal of Southwest Jiaotong University, 2011,46(5):868-874.]
[7]余孝军,黄海军,刘天亮.固定需求网络中多用户类随机均衡的效率损失[J].交通运输系统工程与信息, 2009,9(4):83-89.[YU X J,HUANG H J,LIU T L.Effi⁃ciency loss of the multi-class stochastic traffic equilibri⁃um assignment with fixed demand[J].Journal of Trans⁃portation Systems Engineering and Information Technol⁃ogy,2009,9(4):83-89.]
[8]徐兵,朱道立.多用户多准则固定需求随机交通均衡变分模型[J].公路交通科技,2007,24(4):129-133. [XU B,ZHU D L.A multiclass and multicriteria stochas⁃tic traffic network equilibrium variational inequality model with fixed demand[J].Journal of Highway and Transportation Research and Development,2007,24(4): 129-133.]
[9]Kenneth E Train.Discrete choice methods with simula⁃tion(the Second Edition)[M].United States of America: Cambridge University Press,2003.
[10]Chieh-Hua Wen,Frank S Koppelman.The generalized Nested logit model[J].Transportation Research Part B, 2001,35(7):627-641.
[11]McFadden D.Modelling the choice of residential location [M].Institute of Transportation Studies,University of California,1978.
[12]Bekhor S,J N Prashker.Stochastic user equilibrium for⁃mulation for generalized Nested logit model[J].Transpor⁃tation Research Record:Journal of the Transportation Research Board,2001,1752:84-90.
[13]Yang H,Huang H J.The Multi-Class,Multi-criteria traffic network equilibrium and systems optimum prob⁃lem[J].Transportation Research Part B,2004,38(1):1-15.
[14]Bekhor S,Reznikova L,Toledo T.Application of crossnested logit route choice model in stochastic user equi⁃librium traffic assignment[J].Transportation Research Record:Journal of the Transportation Research Board, 2007,2003(1):41-49.
Multi-Class and Multi-Criteria Stochastic User Equilibrium Model Based on Generalized Nested Logit Model
LI Xue-fei,LANG Mao-xiang
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University,Beijing 100044,China)
ract:This paper focuses on the multi-class,multi-criteria stochastic user equilibrium model based on the generalized nested logit model.The basic theory of generalized nested Logit model is introduced and the multi-class users with different value of times are considered.Then the equivalent mathematical programming model for the multi-class,multi-criteria stochastic user equilibrium model based on the generalized nested Logit model is set up and the equivalence and uniqueness conditions are proved.The path-based method of successive averages(MSA)algorithm is designed to solve the proposed mathematical programming model and the effectiveness of the proposed algorithm is verified in a numerical example.The influences of dispersion parameter with different values on the traffic assignment results are analyzed and the assignment result is compared with that of MNL model.The results of the numerical example show that the proposed model can overcome the IIAproperty of the MNL model and the proposed algorithm has high efficiency.
rds:urban traffic;SUE;MSA;generalized nested Logit;multi-class;multi-criteria
1009-6744(2014)04-0139-07
U491.1
A
2013-11-12
2014-02-18录用日期:2014-03-10
中央高校基本科研业务费专项资金资助(2012YJS054).
李雪飞(1986-),男,内蒙古呼和浩特市人,博士生. *
mxlang@bjtu.edu.cn

