应急物资保障系统模糊多目标LARP研究

陈刚，张锦*，付江月

应急物资保障系统模糊多目标LARP研究

陈刚a,b，张锦*a,b，付江月a,b

（西南交通大学a.交通运输与物流学院；b.综合交通运输智能化国家地方联合工程实验室，成都610031）

为了将应急物资快速有效地配送至灾区，从供应链的角度构建一个包含应急物资供应点、集散点、配送中心及受灾点四层结构的应急物资保障系统.在考虑需求不确定性的基础上建立一个双层优化模型.上层模型以最晚运达时间最小、配送总成本最小及车辆载重利用率最大为目标，决策灾区应急物资配送中心的选址及车辆路径安排；下层模型以运输总成本最小为目标，决策应急物资集散点的选址及应急物资的分配.设计一种自适应遗传算法求解上层模型，运用GAMS软件求解下层模型.以“4·20”四川芦山地震应急物资保障为背景构建算例，验证模型和算法的可行性和有效性.

物流工程；多目标优化；自适应遗传算法；选址-分配-路径问题；模糊需求

1 引言

随着地震、台风、海啸等自然灾害的频繁发生，应急物流受到广泛关注.已有不少学者研究了应急设施选址(facility location)问题[1，2]、应急物资分配(resource allocation)问题[3-5]及应急车辆路径(vehicle routing)问题[6-8]；还有的学者对以上三个问题的其中某两个进行了集成优化，研究了应急物流系统中的LAP(location-allocation problem)[9，10]、ARP(allocation-routing problem)[11，12]及LRP(location-routing problem)[13-15].以上研究都只考虑了应急物流的一个或两个环节，并未从整个系统的角度进行优化.而应急设施选址、物资分配及运输路线安排问题并非相互独立，有必要对其进行集成优化.因此，本文借鉴供应链的思想研究了应急物流系统中的LARP(location-allocation-routing problem).

自然灾害的突发性及救援时间的紧迫性往往造成应急物资需求的不确定性，同时还应考虑应急物资配送的时间效益和经济效益.为此，本文提出了一个包含应急物资供应点、集散点、配送中心及受灾点四层结构的应急物资保障系统，其中集散点及配送中心为临时应急设施，需要对其进行定位选址.基于该系统构建了一个双层优化模型：上层模型——决策灾区应急物资配送中心的选址及车辆路径安排，下层模型——决策应急物资集散点的选址及应急物资的分配.上层模型以最晚运达时间最小、配送总成本最小及车辆载重利用率最大为目标，下层模型以运输总成本最小为目标.设计了一种自适应遗传算法求解上层模型，并运用GAMS(general algebraic modeling system)软件求解下层模型.最后以“4·20”四川芦山地震为背景构建算例对模型及算法进行分析.

2 问题描述

为了将应急物资快速准确地配送至灾区，构建了灾后应急物资保障系统，如图1所示.该系统是一个由四级设施构成的多层次复杂网络，网络中的供应点、集散点、配送中心及受灾点都是多对多的关系.灾区外围需要解决的是集散点选址问题及它与上游节点(供应点)和下游节点(配送中心)应急物资分配问题，该阶段应急物资运输量大，路程远，都是采用整车直运.灾区内部需要解决的是配送中心选址及配送车辆路线安排问题，该阶段应急物资运输量小，路程短，往往采用巡回配送.由于灾后通信不畅，无法获得受灾点准确的需求信息，但根据经验可以知道受灾点需求量的一个范围，故可采用区间数表示受灾点的需求量.

因此，本文研究的问题可描述为在应急物资需求不确定的情况下，制定一套应急物流方案，解决临时应急设施选址、应急物资分配及配送车辆路线安排问题.

图1 灾后应急物资保障系统Fig.1 Urgent relief distribution system in post-disaster

3 模型构建

3.1 符号说明

(1)集合.

S表示所有点的集合，i,j∈S；G为受灾点的集合，g∈G；H为应急物资配送中心的集合，h∈H；N为应急物资集散点的集合，n∈N；M为应急物资供应点的集合，m∈M；S1=H⋃N⋃M，S2=G⋃H，S3=H⋃N，S4=N⋃M；P为车辆类型的集合，p∈P；K为灾区配送中心救援车辆的集合，k∈K.

(2)参数.

q～i为受灾点i(i∈G)的应急物资需求量，用区间数为点i到点j的距离；vij为点i到点j之间车辆的平均行驶速度；tij为救援车辆从点i到点j的行驶时间，tij=dij/vij；Ti为救援车辆到达点i(i∈S2)的时间，当i∈H时Ti=0；NVip为应急设施i拥有类型p车辆的数量，i∈S4；CVp表示类型p车辆的最大载重量；Qk表示灾区配送车辆k的最大载重量；cij表示从点i到点j单位物资单位距离的运输成本；Capi表示临时应急设施i的处理能力，i∈S3；Fi表示开放临时应急设施的固定费用，i∈S3；CFn表示集散点n单位物资的中转成本；Supm表示供应点m的应急物资储备量；λ1表示配送车辆容量限制的满意水平，λ1∈[0,1]；λ2表示配送中心处理能力的满意水平，λ2∈[0,1]；λ3表示供给不小于配送中心需求的满意水平，λ3∈[0,1].表示

(3)决策变量.

xijk∈{0,1}，取1时表示车辆k从点i驶向点j，i,j∈S2,i≠j，否则取0；yh∈{0,1}，取1时表示备选点h被选为配送中心，否则取0；zn∈{0,1}，取1时表示备选点n被选为集散点，否则取0；fij表示点i到点j的应急物资运输量，i,j∈S1.其中xijk与yh为上层模型的决策变量，zn与fij为下层模型的决策变量.

3.2 模型构建

上层模型决策灾区应急物资配送中心的选址及车辆路径安排，为灾区现场应急救援指挥中心提供辅助决策支持.下层模型决策应急物资集散点的选址及应急物资的分配，为国家应急救援指挥中心提供辅助决策支持.决策目标为在资源有限的条件下，花费较少的费用在最短的时间内将应急物资送到灾区人民手中.上层模型的决策结果将影响下层模型部分参数的取值，进而影响其决策结果.

上层决策模型：

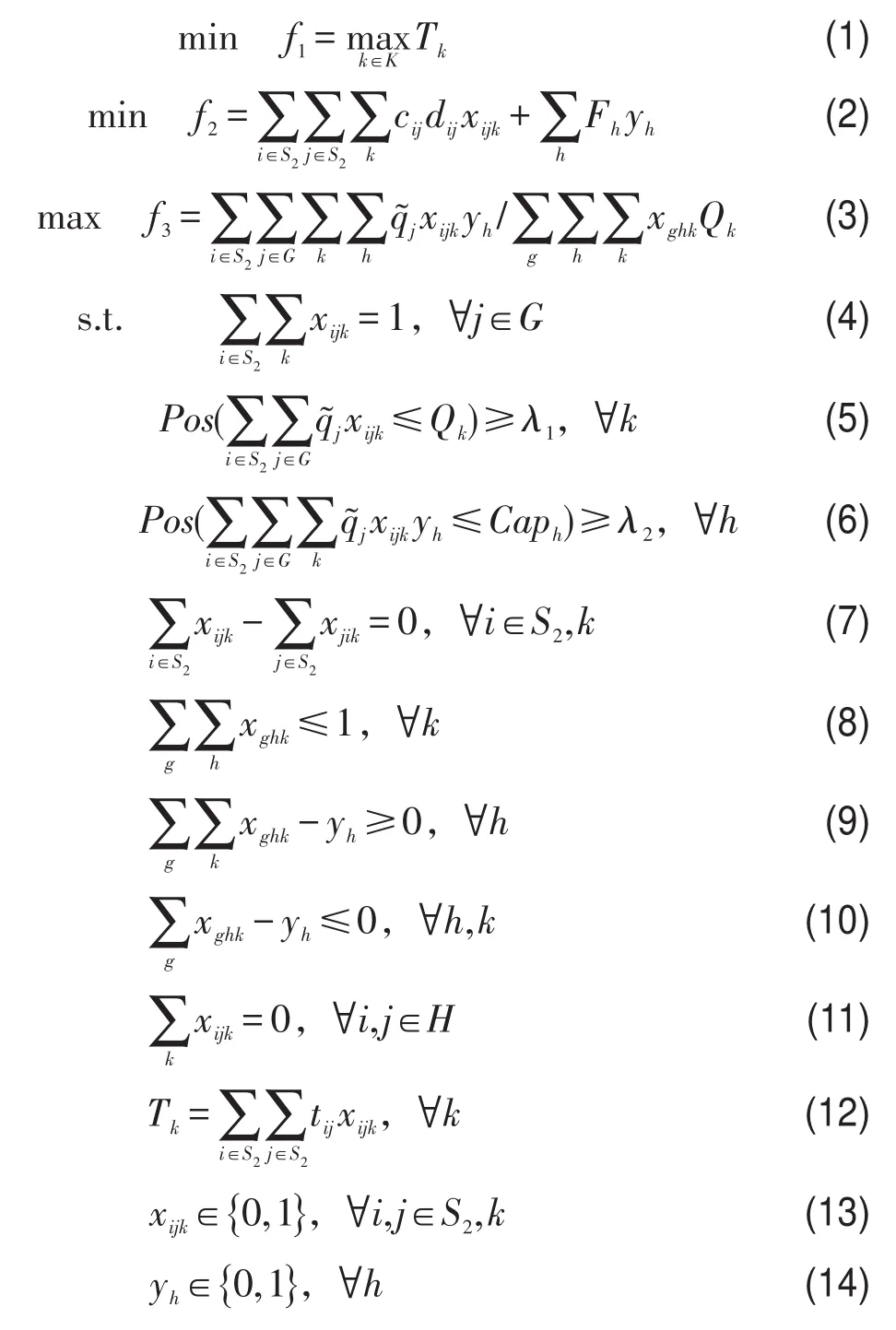
目标函数式(1)表示最小化配送车辆最晚运达时间，保证受灾点都能在最短的时间内收到应急物资；式(2)表示最小化配送的总成本，包括车辆的运输成本和配送中心的开放成本；式(3)表示最大化车辆的载重利用率.约束式(4)表示每个受灾点有且只有一辆车为其配送；式(5)表示满足车辆容量约束的满意水平不小于λ1；式(6)表示满足配送中心容量约束的满意水平不小于λ2；式(7)表示车辆路径连续；式(8)表示每辆车只属于一个配送中心；式(9)表示选中的配送中心至少有一辆车发出；式(10)表示未选中的配送中心不发车；式(11)表示配送中心之间不转运；式(12)为Tk的数学表达式；式(13)-式(14)为自变量约束.

下层决策模型：

目标函数式(15)表示整车直运的总成本最小，其中第一、二项为运输成本，第三项为集散点的开放成本和应急物资中转成本.约束式(16)表示供应点的供应量不大于其储备量；式(17)、式(21)表示运输车队运力的限制，式(18)表示集散点处理能力的限制，式(19)表示集散点的流量守恒，式(20)表示物资供应量满足灾区配送中心需求量的满意水平不小于λ3，式(22)-式(23)为自变量约束.

3.3 模糊约束条件的处理

由于约束条件式(5)、式(6)、式(20)具有模糊参数q～j，无法直接计算，需要进行一定的处理.

定义1[16][a,b]为区间数，当a,b∈R,a≤b.设[a-,a+],[b-,b+]为区间数，其算术运算定义如下：

定义2[16]设A=[a-,a+]为区间数，b为实数，记len(A)=a+-a-，则称

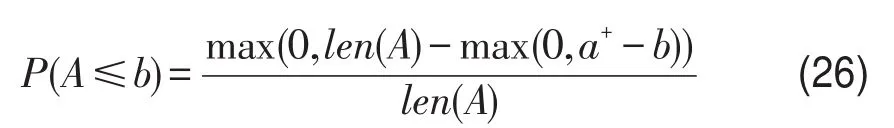
为A≤b的可能度.

定义3[17]设A=[a-,a+]为区间数，b为实数，给定数λ∈[0,1]，若P(A≤b)≥λ成立，则称不等式A≤b的满足水平为λ.

定理设A=[a-,a+]为区间数，b为实数，对于任意λ∈[0,1]，满足水平为λ的模糊不等式A≤b等价于清晰化不等式

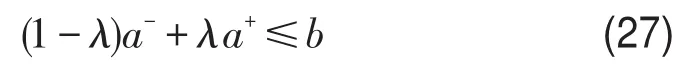
证明由于λ∈[0,1]，根据式(26)得len(A)-max(0,a+-b)≥λlen(A)，从而得到(1-λ)(a+-a-)≥max(0，a+-b)，若a+-b＜0，不等式恒成立；若a+-b≥0，不等式等价于(1-λ)a-+λa+≤b，定理得证.

根据定理可将模糊约束条件式(5)、式(6)、式(20)转化为清晰化的约束条件式(28)-式(30)：

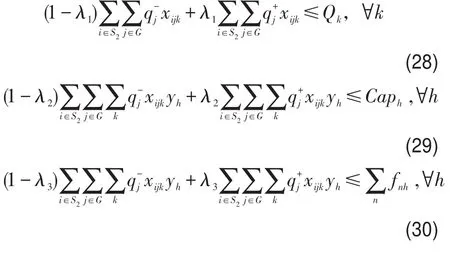
4 模型求解

设计自适应遗传算法求解上层模型，采用GAMS编程求解下层模型.遗传算法具有很强的全局搜索能力和隐含的并行性，其选择、交叉、变异等遗传操作保证了算法的收敛性.GAMS的求解引擎采用分支切割法，能求出混合整数规划(MIP)模型的最优解，进而保证算法的收敛性.两个算法之间的参数传递保证了算法的统一性.

4.1 自适应遗传算法

(1)染色体编码.

每条染色体由两个子串组成：子串1有G个基因位(G为受灾点的数目)，其中每个基因位的取值为1～K的自然数中随机选取一个(K为配送车辆数目)，表示各需求点由哪一辆车服务；子串2有K个基因位，每个基因位的取值为1～H的自然数中随机选取一个(H为配送中心的数目)，表示各配送车辆分配给哪一个配送中心，因此，染色体的长度为G+K.

(2)种群初始化.

设种群规模为popsize，按照编码方案随机产生满足约束条件的个体，如果不满足约束条件则重新产生新个体直到满足约束，产生popsize个满足约束条件的个体作为初始种群.

(3)适应度函数设置.

适应度函数可通过变换目标函数得到，由于目标函数量纲不同，需要进行归一化处理.首先，计算同一代种群中每条染色体的三个目标函数值及其中最大值和最小值分别记为则每条染色体的适应度为

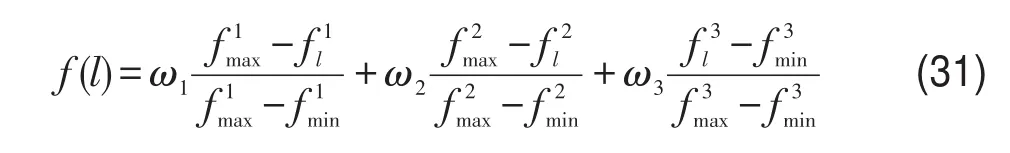
式中ωi(i=1,2,3)为各目标适应度函数值的权重，ω1+ω2+ω3=1.

(4)遗传操作设置.

采用轮盘赌选择与保留精英相结合的策略，使得适应度大的个体有较大概率进入下一代.采用自适应多点交叉，交叉概率为pc1和pc2(pc1＜pc2)，当个体适应度小于等于种群的平均适应度时交叉概率为pc2，否则为pc1.采用自适应单点变异，变异概率为pm1和pm2(pm1＜pm2)，当个体适应度小于等于种群的平均适应度时变异概率为pm2，否则为pm1.

将通过遗传操作得到的临时种群与父代种群组合成新的种群，计算种群适应度并排序，将适应度高的popsize个体作为父代进入下一次遗传操作.

(5)终止条件.

设置最大迭代次数为genmax，遗传算法迭代genmax次后结束.

4.2 GAMS软件建模

GAMS是一种面向应用的构造模型的高级计算机语言，融合了关系数据库技术与数学规划理论，包含了编译器和高效能的求解引擎，能有效地求解LP、NLP、MIP、NMIP等类型的数学规划问题. GAMS建模采用的术语如下：索引称为集合(sets)，已知数据称为参数(parameters)，决策变量称为变量(variables)，约束和目标函数称为方程(equations).本文构建的下层决策模型是一个MIP模型，故采用GAMS软件对其进行建模，并通过“solve”语句调用CPLEX求解引擎求解模型并输出结果.

5 算例分析

以“4·20”四川芦山地震应急物资保障为例，成都、武汉等10地为应急物资供应点(编号为1-10)，成都市的青白江物流园区、新津物流园区等5地为备选应急物资集散点(编号为11-15)，雅安市的雨城区、名山县等5地为灾区备选的应急物资配送中心(编号为15-20)，芦阳镇、太平镇等30地为受灾点(编号为21-50).供应点与受灾点信息如表1所示，集散点及配送中心信息如表2所示，救援车辆信息如表3所示，其中供应点各拥有1辆P2类型的货车，集散点各拥有2辆P3类型的货车，灾区有10辆P1类型的配送车辆.满意水平λ1，λ2，λ3=0.95，由于篇幅限制，其它参数不再列出.

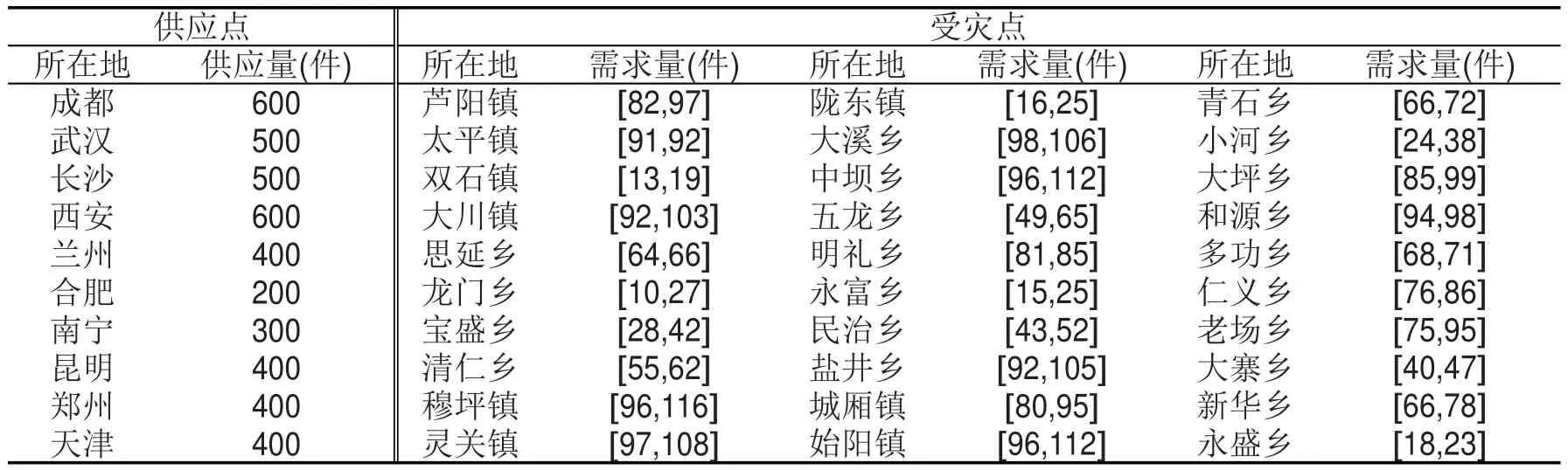
表1 供应点与需求点信息Table 1 The information of supply depots and affected areas

表2 集散点与配送中心信息Table 2 The information of transshipment depots and distribution centers

表3 救援车辆信息Table 3 The information of relief vehicles

根据上述设计的自适应遗传算法求解上层模型，设种群规模popsize=1 000，代沟率GGAP=1，最大迭代次数genmax=500，交叉概率为pc1=0.7、pc2=0.9，变异概率为pm1=0.005、pm2=0.01，ω1=0.7、ω2=0.2、ω3=0.1.通过MATLAB R2011b软件编程，在Inter Core i3 550@3.20GHz CPU，4.00GB内存配置的电脑上运行程序耗时265.06 s，得出加权的目标函数（适应度）最优值为0.661 9，三个目标函数最优值分别为其配送中心选址及路线安排决策结果如表4所示.

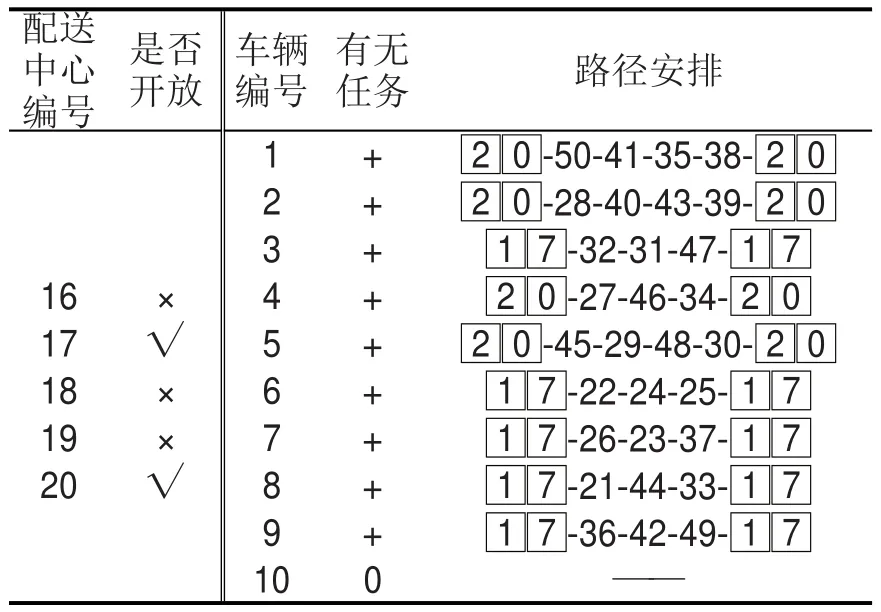
表4 配送中心选址及路线安排决策结果Table 4 The solution of location of distribution centers and vehicle routing

算法的性能跟踪如图2所示，在第262代后，适应度趋于某值，算法迅速收敛，但各目标相互冲突，不可能使所有的目标达到最优，只能优先保障重要的目标.由于灾难救援中应急物资的快速响应是保障灾民生命安全的重要条件，必须在最短的时间内将应急物资送到灾民手中，所以算法牺牲了目标函数3（载重利用率），启用更多的车辆以满足在最短的时间内完成应急物资的配送任务.

在其他参数不变的情况下，取交叉概率为0.7，变异概率为0.005，采用基本遗传算法进行计算，运行程序10次并取其最优结果，基本遗传算法与自适应遗传算法的性能对比如表5所示.可以看出自适应遗传算法比基本遗传算法的适应度提高了24.46%，而计算时间只增加了2.43%.三个目标函数值得到进一步优化：最晚运达时间减小了41.46%，配送总成本减少了5.84%，车辆载重利用率提高了11.12%.因此，本文提出的自适应遗传算法具有一定的可行性和有效性.

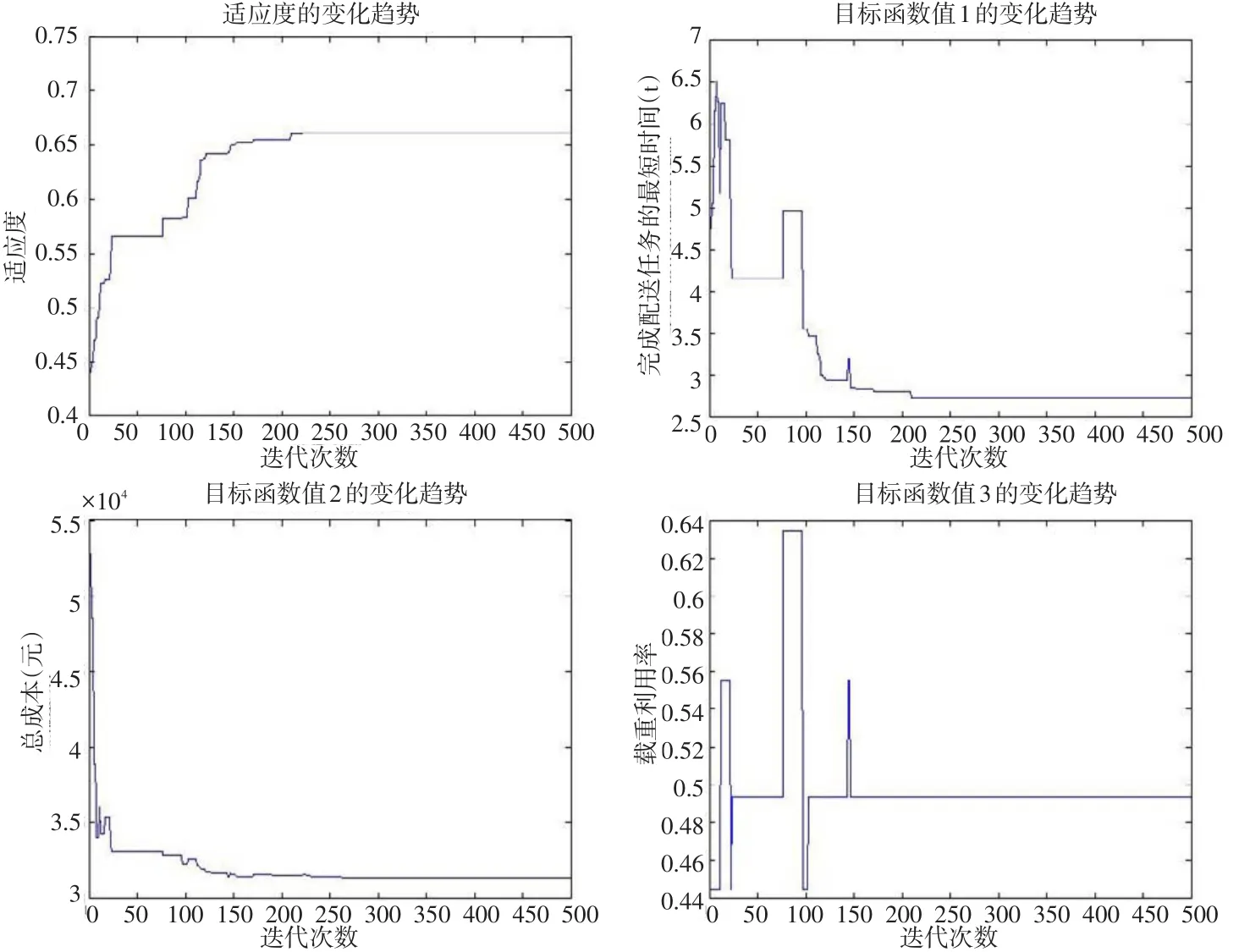
图2 自适应遗传算法性能跟踪图Fig.2 Self-adaptive genetic algorithm performance tracing

表5 基本遗传算法与自适应遗传算法的性能对比Table 5 Comparison of the basic genetic algorithm and self-adaptive genetic algorithm

根据上层模型的决策结果，采用GAMS软件对下层模型进行建模，并调用CPLEX求解引擎求解.其中模型参数301个，变量66个，方程83个，经过211次迭代，计算时间0.42 s，得出最优目标函数值为165 455.2.集散点选址及应急物资分配决策结果如图3所示，集散点选址结果为新津物流园区与龙泉物流中心，启用的供应点为成都、武汉、西安、兰州、昆明救灾物资储备库.

研究表明，本文提出的应急物资保障系统的模型能够反映灾后应急物资从供应点到需求点的整个供应链过程，具有较好的实用性，求解算法具有较好的收敛性和有效性，能为应急管理部门提供辅助决策支持.

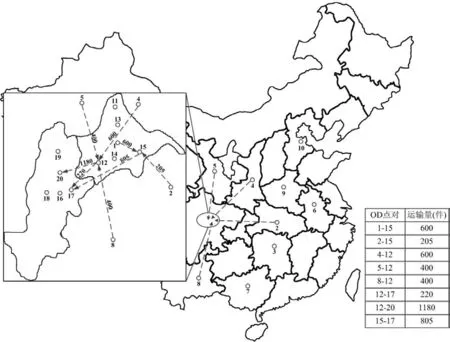
图3 集散点选址及应急物资分配决策结果Fig.3 The solution of location of transshipment depots and relief commodities allocation

6 研究结论

本文综合考虑灾区应急物资需求的不确定性及配送的时间效益与经济效益，采用双层优化决策方法进行应急物资保障.上层模型以最晚运达时间最小、配送总成本最小及车辆载重利用率最大为目标，决策灾区应急物资配送中心的选址以及车辆路径安排；下层模型以运输总成本最小为目标，决策应急物资集散点的选址及应急物资的分配.设计了包含保留精英策略的自适应遗传算法求解上层模型，运用GAMS编程求解下层模型，并以“4·20”四川芦山地震应急物资保障为背景构建算例对模型和算法进行了验证.结果表明，算法具有较好的收敛性和有效性，能在较短的时间内得到一个近似最优解供决策者参考.此外，本文提出的应急物资保障系统能够反映灾后应急物资从供应点到需求点的整个供应链过程，具有较好的实用性.本文解决多目标的方法是将其转化为单目标，虽然可以通过改变权重得到多目标问题的多个非劣解，但操作相对复杂，进一步将结合NSGAⅡ算法研究应急物流系统中多目标问题的Pareto解.

[1]Canbolat M S,Massow M.Locating emergency facilities with random demand for risk minimization[J].Expert Systems with Applications,2011,38(8):10099-10106.

[2]Murali P,Ordonez F,Dessouky M.Facility location un⁃der demand uncertainty:response to a large-scale bioterror attack[J].Socio-Economic Planning Sciences, 2012,46(1):78-87.

[3]Sheu J B.An emergency logistics distribution approach for quick response to urgent relief demand in disasters [J].Transportation Research Part E:Logistics and Trans⁃portation Review,2007,43(6):687-709.

[4]詹沙磊,刘南.基于灾情信息更新的应急物资配送多目标随机规划模型[J].系统工程理论与实践,2013,33 (1):159-166.[ZHAN S L,LIU N.Multi-objective sto⁃chastic programming model for relief allocation based on disaster scenario information updates[J].Systems En⁃gineering-Theory&Practice,2013,33(1):159-166.]

[5]王恪铭,马祖军,周愉峰.突发事件应急血液调剂问题的两阶段决策方法[J].交通运输系统工程与信息, 2013,13(1):169-178.[WANG K M,MA Z J,ZHOU Y F.A two-phase decision-making approach for emergen⁃cy blood transferring problem in public emergencies[J]. Journal of Transportation Systems Engineering and Infor⁃mation Technology,2013,13(1):169-178.]

[6]Jotshi A,Gong Q,Batta R.Dispatching and routing of emergency vehicles in disaster mitigation using data fu⁃sion[J].Socio-Economic Planning Sciences,2009,43 (1):1-24.

[7]Huang M,Smilowitz K R,Balcik B.A continuous approx⁃imation approach for assessment routing in disaster relief [J].Transportation Research Part B:Methodological, 2013,50:21-41.

[8]Ozdamar L,Demir O.A hierarchical clustering and rout⁃ing procedure for large scale disaster relief logistics planning[J].Transportation Research Part E:Logistics and Transportation Review,2012,48(3):591-602.

[9]Najafi M,Eshghi K,Dullaert W.A multi-objective ro⁃bust optimization model for logistics planning in the earthquake response phase[J].Transportation Research Part E:Logistics and Transportation Review,2013,49 (1):217-249.

[10]刘亚杰,雷洪涛,郭波.地震灾害救援动员中的选址分配模型与算法[J].控制与决策,2013,28(1):78-83. [LIU Y J,LEI H T,GUO B.Facility location-allocation model and algorithm for mobilization of earthquake di⁃saster relief[J].Control and Decision,2013,28(1):78-83.]

[11]Barbarosoglu G,Arda Y.A two-stage stochastic pro⁃gramming framework for transportation planning in di⁃ saster response[J].Journal of the Operational Research Society.2004,55(1):43-53.

[12]陈刚,张锦,彭永涛.震后应急物资敏捷保障体系模型及算法[J].自然灾害学报,2013,22(3):47-53.[CHEN G,ZHANG J,PENG Y T.Agile security model and algo⁃rithm for post-earthquake urgent relief provisons[J]. Journal of Natural Disasters,2013,22(3):47-53.]

[13]Yi W,Kumar A.Ant colony optimization for disaster re⁃lief operations[J].Transportation Research Part E:Logis⁃tics and Transportation Review,2007,43(6):660-672.

[14]Afshar A,Haghani A.Modeling integrated supply chain logistics in real-time large-scale disaster relief opera⁃tions[J].Socio-Economic Planning Sciences,2012,46 (4):327-338.

[15]王绍仁,马祖军.震害紧急响应阶段应急物流系统中的LRP[J].系统工程理论与实践,2011,31(08):1497-1507.[WANG S R,MA Z J.Location-routing problem in emergency logistics system for post-earthquake emer⁃gency relief response[J].Systems Engineering—Theory &Practice,2011,31(08):1497-1507.]

[16]郭子雪,齐美然,张强.基于区间数的应急物资储备库最小费用选址模型[J].运筹与管理,2010,19(1):15-20.[GUO Z X,QI M R,ZHANG Q.Minimum cost mod⁃el of emergency material storage location based on inter⁃val number[J].Operations Research and Management Science,2010,19(1):15-20.]

[17]魏国强,余超.带模糊参数的战时紧缺资源调度模型[J].计算机工程与应用,2013,49(12):246-249.[WEI G Q,YU C.Battlefield dispatching model of scare mili⁃tary supplies with fuzzy parameters[J].Computer Engi⁃neering and Applications,2013,49（12）：246-249.]

Multi-objective Fuzzy Location-allocation-routing Problem in Urgent Relief Distribution System

CHEN Ganga,b,ZHANG Jina,b,FU Jiang-yuea,b
(a.School of Transportation and Logistics;b.National United Engineering Laboratory of Integrated and Intelligent Transportation,Southwest Jiaotong University,Chengdu 610031,China)

ract:To distribute the urgent relief commodities to the disaster areas with high efficiency,this study proposes a four-layer urgent relief distribution system consisting supply depots,transshipment depots,distribution centers and affected areas,from the perspective of supply chain.A bi-level optimization model is proposed with consideration of the uncertain demand.The location of distribution centers and the route scheduling of delivery vehicles are determined by the upper model with the goals of minimizing the last arrival time and the total delivery cost,as well as maximizing the vehicle load utilization.The location of transshipment depots and allocation of relief commodities are decided by the lower model with the goal of minimizing the total transportation cost.A self-adaptive genetic algorithm is also proposed to solve the upper model,and the GAMS is employed to solve the lower model.A numerical example of“4·20”Sichuan Lushan earthquake of China is presented to verify the feasibility and effectiveness of the model and algorithm.

rds:logistics engineering;multi-objective optimization;self-adaptive genetic algorithm;locationallocation-routing problem;fuzzy demand

1009-6744（2014）04-0160-08

F252;C931

A

2013-10-26

2014-02-18录用日期：2014-03-25

国家社会科学基金资助项目(11BJL054).

陈刚（1987-），男，四川岳池人，博士生. *

zhjswjtu@swjtu.cn