数据驱动航空收益管理舱位分配研究*
王 霄
(陕西工业职业技术学院 物流管理学院,咸阳 712000)
航空收益管理技术是航空运输领域一项重要技术。全球90%以上的航空公司均采用这一技术。在收益管理舱位分配方面,国外有研究单航节的优化方法,假设低价格舱位先于高价格舱位被旅客预订,研究两种价格的舱位分配问题,提出基于两种价格舱位的单航节期望边际收益原则[1]。把单航节两舱位的期望边际收益原则扩展到多个舱位,提出相应算法,被广泛采用[2]。文献[3]提出一个连续时间的动态随机规划模型,该模型表明最低限度的舱位分配策略最优。文献[4]提出一个随机分配模型,以此动态分配舱位。对于不同价格或等级的舱位预订,遵循严格到达顺序的假设下,在静态的舱位预订限制条件下考虑最优的预订策略,提出预订限制的算法[5]。文献[6]提出动态规划模型决定最优动态预订分配策略。舱位分配是收益管理的核心,舱位分配建立在对市场需求精准预测的基础上。目前,国内外有关收益管理理论大部分建立在假定需求分布已知,或者直接假定需求为确定的前提下,然而预测需求和现实需求之间的差距很大[7]。文献[8]将航空公司乘客到达的具体数据同泊松分布、伽玛分布以及负二项式分布进行对照和匹配,结果发现伽玛分布与实际情况较为吻合。需求预测的主要方法有统计方法和随机过程方法两类。通过均匀或非均匀和混合的泊松过程,建立需求到达的随机过程模型[9-11],计算得出的预测需求舱位数量与实际差距很大,舱位需求数量具有不确定性。
本文针对舱位需求数量不确定这一现实问题研究国内普通中型飞机航班舱位收益,引入数据驱动的理论方法对舱位分配进行优化,以期降低舱位需求不确定性对单航节期望收益的不良影响。引入修正因子这一标量参数,根据对历史需求数据的信心程度对修正因子赋值,剔除部分不良数据,对舱位收益管理进行探析。
1 数据驱动基本理论
需求不确定是收益管理需要解决的核心问题,由于大部分理论均为假设需求分布已知,决策者风险中立,在实际当中,需求数量很难精准预测。应用数据驱动方法在优化理论领域,将传统报童问题进行扩展,旨在降低需求不确定性[12]。
在收益管理情境下,关注收益π(Q,D),其中Q为订购量,D为不确定需求。假设需求观测总数量N个,观测值分别为d1,d2,…,dk,…,dN,使其按递增顺序排列得:d(1)≤d(2)≤…≤d(k)≤…≤d(N),有
(1)
式中:α为修正因子(风险系数),且α∈[0,1];Nα为修剪后的观测值总数,Nα=[N(1-α)+α];当α=0,有Nα=N,即保留了全部数据,表明决策者具有更低的风险厌恶态度;当α=1,有Nα=1,此时只保留了最坏的数据,表明决策者具有更高的风险厌恶态度。α值反映决策者风险厌恶程度,此时风险系数α为可控。同时,保证Nα能够取遍从1到N的所有数值。即当α∈[0,1]时,Nα={1,2,…,N}。
π(Q,d)(k)是指从小到大排在第k位的收益,dk≥0 (k=1,2,…,N)且为整数。问题的关注点为求解下式:
s.t.Q∈Ω
(2)
其中Ω为订购量Q的可行集,设为凸的。
选择可行集Q∈Ω,将π(Q,d)(k)按照从小到大排列,取前Nα个收益的均值,计算得出收益最大的Q。
有定理1为凸规划问题,π(Q,D)在Q是凹的。
定理1 数据驱动问题
式(2)等价为
(3)
当π(Q,D)在Q是凹的,式(3)为一个凸问题;当π(Q,D)为分段线性函数,在Q是凹的,且Ω是一个多面体,式(3)为一个线性规划问题。
证明:
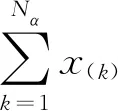
(4)
式(4)的可行集是非空有界的,因此式(4)的对偶问题可表示为
s.t.φ+ψk≤xk,∀k
ψk≤0, ∀k
(5)
将式(5)及xk=π(Q,dK)代入式(2),得到式(3)。
2 两价格同等级舱位分配模型
2.1 需求独立正态分布下的分配模型
借鉴文献[13]分配方案。假定舱位同质,即舱位为同等级,或为商务舱位或为经济舱位,其价格分为全价和折扣价两种。且全价舱位的需求量服从正态分布,计算最优的折扣价舱位预订限额为
(6)
式中:Φ(x)为标准累积正态分布;μf和σf分别为全价舱位需求量的均值和标准差,全价舱位和折扣舱位的价格分别为Pf和Pd,且Pf>Pd。根据李特尔伍德法则,要找到一个折扣价舱位预留限额b值,使得
(7)
有最优折扣价舱位的预订限额b*,使得全价舱位的保留数量即保留水平y*得以满足,C为舱位总数,有
b*=[C-σfΦ-1(1-Pd/Pf)-μf]+
(8)
y*=min[μf+σfΦ-1(1-Pd/Pf),C]
(9)
其中Φ-1(x)为逆累积正态分布。
单独分析Φ-1(x),得到如下结论:
Φ-1(1-Pd/Pf)为价格比率Pd/Pf的函数,同时和式(9)讨论,分析推导出关于最优折扣舱位预订限额的相关特性。
Φ-1(1-Pd/Pf)为Pd/Pf的减函数,即当价格比率提高,Φ-1(1-Pd/Pf)将会变小,b*为价格比率的增函数。
若Φ-1(1/2)=0,即Pd=Pf/2,b*=C-μf。有Pd/Pf=1/2,全价舱位的保留水平等于全价舱位需求的均值。
当Pd/Pf<1/2,全价舱位的保留水平大于全价舱位需求的均值;当Pd/Pf>1/2,全价舱位的保留水平小于全价舱位需求的均值。
全价舱位的保留水平由价格比率决定。
2.2 数据驱动下的分配模型
给定航班舱位数量,将舱位分配给不同价格,使舱位利用率最大,实现收益最大化[14]。由李特尔伍德法则分析得知,全价舱位的最优保留水平与折扣价舱位需求有关。即把折扣价舱位需求预测加倍或者减半均影响最优的全价舱位预订限额。在两价格舱位分配时,假设折扣价舱位的需求是无限的,即舱位一定会被预订。具体分析如下:
当全价舱位的需求df小于等于全价舱位的保留水平y时,此时航班只能提供需求的舱位数量,当全价舱位的需求df大于全价舱位的保留水平y时,此时航班只能满足y的需求。航班全价舱位的期望收益为
π=Pfdf-Pd(C-b),df≤C-b
π=Pf(C-b)-Pd(C-b),df>C-b
(10)
E(π)=Pfmin[df,(C-b)]-Pd(C-b)
(11)
采用数据驱动方法,有Nα=[N(1-α)+α]下的收益最大化公式为
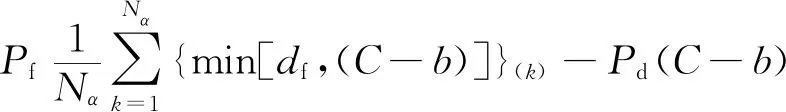
(12)
此时,最优保留水平为目标方程中的一点dj,且dj为整数。因min[df,(C-b)]在其定义域为非递减,满足从小到大排在第k位的min[df,(C-b)]的b,即等价于满足min[d(k),(C-b)]。求解为

(13)
式(13)最优保留水平y的解即最优解,满足

(14)
证明:
当d(k)≤y≤d(k+1),Pfk/Nα≤Pd,最优解为y=d(k);否则,y=d(k+1)。
当y≤d(1)时,最优解y=d(1)。
当y≥d(N)时,最优解y=d(N)。
因此,最优解C-b≥0,且在C-b=d(j)处取得,其中:j/Nα≤Pd/Pf<(j+1)/Nα。
得出结论:最优保留水平可以通过数据驱动的方法得到,且依赖于历史数据的适当排序。对于风险系数(修正因子)α,由于Nα≤N,所以有风险规避者的全价舱位保留水平比风险中立者的保留水平低。
3 两价格及等级舱位分配模拟分析
利用Excel统计软件进行数值模拟,在航班舱位总数一定的前提下,划分两种不同价格及等级舱位,即折扣舱位和全价舱位,假设舱位需求是完全的,即折扣价舱位总能被预订,且折扣价舱位的需求量与全价舱位的需求量之间相互独立。
利用Excel统计软件的数据生成器随机生成100个全价舱位需求数据,且数据为正态分布随机数;假定某固定航线航班拥有舱位共250个,有两种价格等级,全价舱位价格为700元/个。该航班价格比率Pd/Pf分别为0.25,0.50,0.75,分析其最优折扣价舱位限额及全价舱位保留水平。为了便于正态分布与数据驱动的方法进行对比,令α为0,采用所有的需求数据进行处理。
3.1 需求服从独立正态分布下的数值模拟分析
假设全价舱位需求的均值为100个,独立正态分布下两价格舱位分配及总收益情况见表1,从表1看到不同价格比率下标准方差变动时,最优折扣价舱位的限额和全价舱位保留水平以及总收益有变化,其中CV为全价舱位需求变异系数,指需求数据分布离散程度,其变化范围0.1~1.0;STD为标准差;y为折扣价舱位保留水平;b为折扣价舱位限额;R为收益金额。
表1独立正态分布下两价格舱位分配及总收益情况
Tab.1 The airline seat allocationand total revenue of two prices Under independent normal distribution
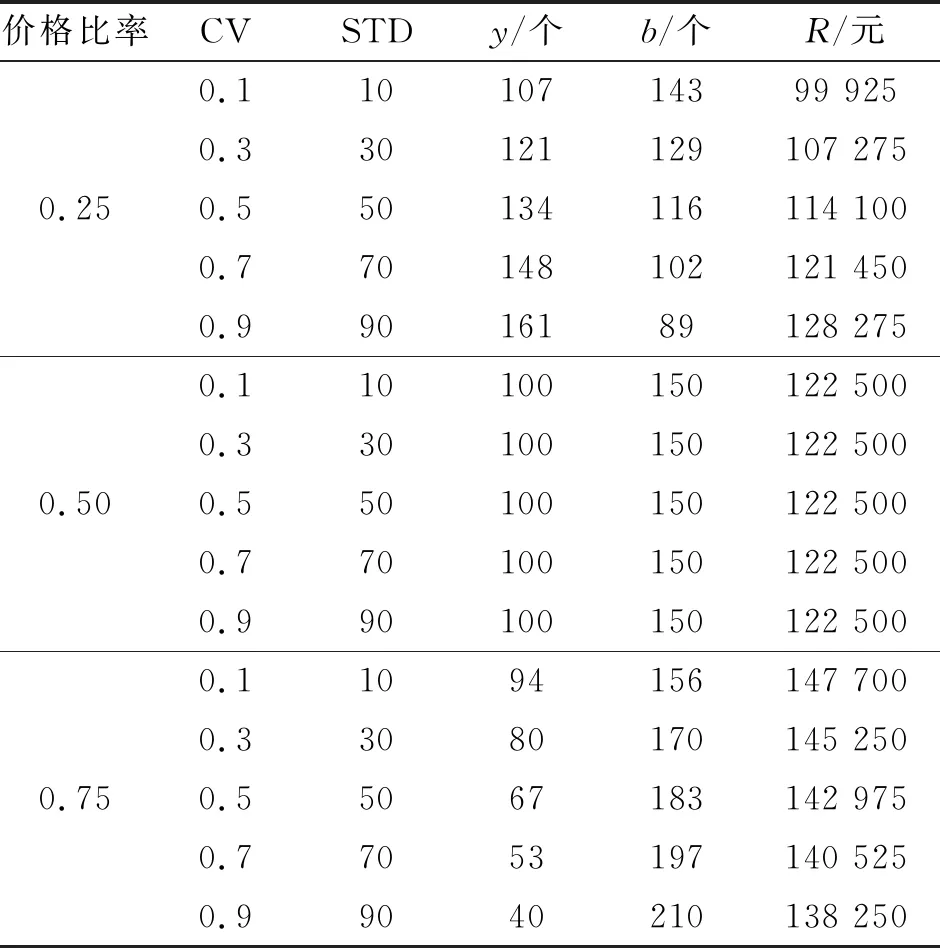
价格比率CVSTDy/个b/个R/元0.110107143999250.3301211291072750.250.5501341161141000.7701481021214500.990161891282750.1101001501225000.3301001501225000.500.5501001501225000.7701001501225000.9901001501225000.110941561477000.330801701452500.750.550671831429750.770531971405250.99040210138250
当全价舱位需求正态分布时,全价舱位预留水平如图1,图1表明不同价格比率下,标准差不同,全价舱位保留水平不同。

图1 独立正态分布下全价舱位预留水平Fig.1 Reserve level about full price cabin Under independent normal distribution
从图1看到,当价格比率为1/2或全价舱位需求的标准差为零时,全价舱位的最优保留水平等于全价舱位需求的均值。若价格比率小于1/2时,全价舱位的最优保留水平将大于全价舱位需求的均值,且增大标准差将会减少折扣价舱位限额。如果价格比率大于1/2时,全价舱位最优保留水平将小于全价舱位需求的均值,且增大标准差,其最优保留水平将会降低。
3.2 数据驱动下的数值模拟分析
设d1,d2,…,dk,…,dN为收集的历史全价舱位需求数据,使其按递增顺序排列得:d(1)≤d(2)≤…≤d(k)≤…≤d(N),假定dk≥0(k=1,2,…,N)且为整数,有a∈[0,1]且α=1-a。令Nα=[N(1-α)+α],保证Nα能够取遍从1到N的所有数值。当α=0,有Nα=N,保留全部的需求数据;当α=1,有Nα=1,只保留最小的需求数据。保留的数据不同表现决策者对历史需求数据的信心程度不同,反映决策者的风险偏好。根据分析得出最优全价舱位的保留水平为
y=d(j),j=[pd/pfNα]
数据驱动下两价格舱位分配及总收益情况见表2,由表2可以看出,在数据驱动下不同价格比率下标准方差变动时,最优折扣价舱位的限额和全价舱位保留水平以及总收益的变化,其中Nα为需求数据个数,j为需求数据的位置顺序,dj为全价舱位需求数据。
数据驱动的处理方法不同于当全价舱位需求正态分布,此时的折扣价舱位限额b并非是标准差的线性函数,其趋势与全价舱位需求服从正态分布时相近,趋近于线性函数。数据驱动下全价舱位预留水平见图2,图2显示了不同的价格比率下,全价舱位的需求在不同标准差下,对最优全价舱位预留水平的影响。

表2 数据驱动下两价格舱位分配及总收益情况Tab.2 The airline seat allocation and total revenue of two prices under data-driven method

图2 数据驱动下全价舱位预留水平Fig.2 Reserve level about full price cabin under data-driven method
从图2可以看出,数据驱动下全价舱位保留水平对全价舱位需求的标准差和价格比率的依赖性,与当全价舱位需求服从正态分布时相近。
3.3 独立正态需求与数据驱动法的对比分析
对比正态分布及数据驱动的计算结果可以发现,对于全价舱位的最优保留水平以及总收益均存在差异,数据驱动的收益高于正态分布的收益。
图3~5为正态分布及数据驱动两种处理方法在不同价格比率下随着数据量的波动幅度变化以及收益对比。
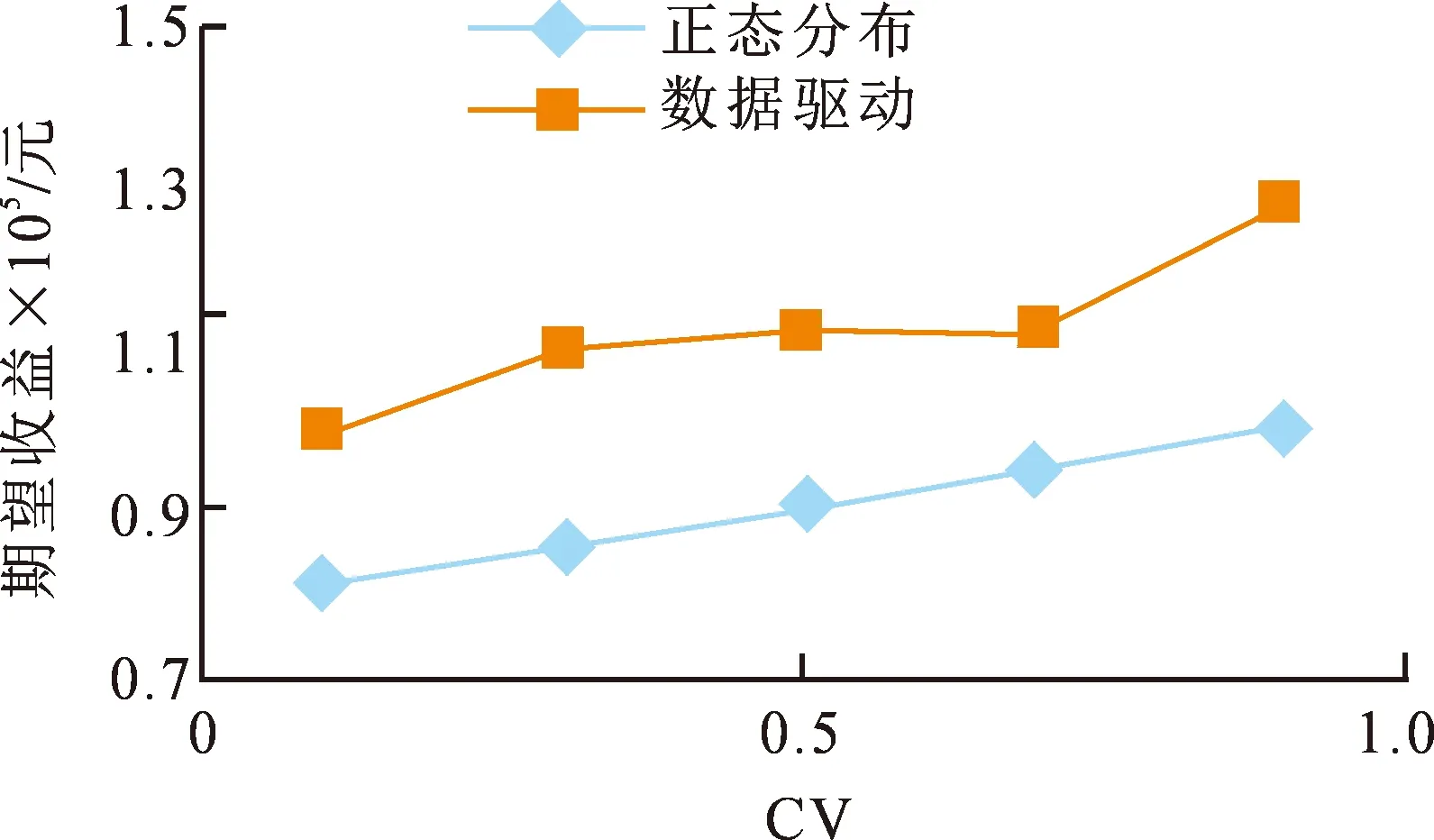
图3 价格比率为0.25的期望收益Fig.3 Expected return with a price ratio of 0.25

图4 价格比率为0.50的期望收益Fig.4 Expected return with a price ratio of 0.50
数据驱动的方法同假设需求服从正态分布的方法分析结果基本一致,两种方法下收益变化大趋势相同,且数据驱动法下的总收益总高于假设需求服从正态分布时的总收益,说明可以采用数据驱动的方法降低需求不确定,获得较高期望收益。
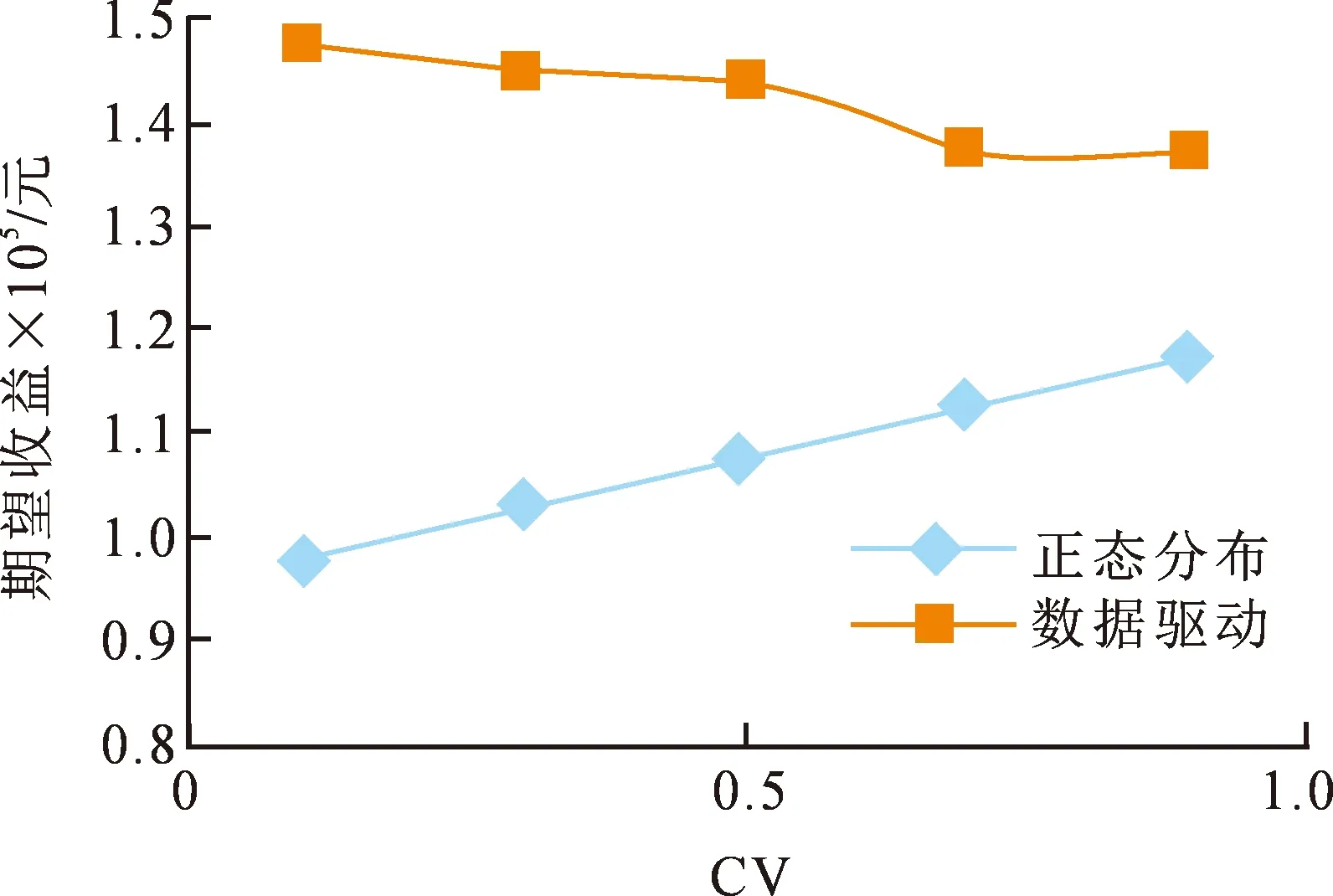
图5 价格比率为0.75的期望收益Fig.5 Expected return with a price ratio of 0.75
4 结 语
两种方法测算的总收益之所以有差异,分析原因有:① 由于数据驱动的方法是通过直接对数据做处理求得最优解,假定需求服从正态分布的方法是对数据进行拟合并求解出最优解;② 两种方法在进行数据处理及求解过程中都会对数据进行四舍五入或取整,数据驱动的方法需要处理的数值较少,处理方法也较为简单,假定需求服从正态分布的方法则需要多次对数值进行处理,都会存在不可避免的差异;③ 数据驱动更符合现实情况,假定需求服从正态分布的方法是在一定假设的基础上获得的,可能与现实情况存在出入。
以数据驱动的方法对舱位分配进行优化。研究结果表明:采用数据驱动方法对历史需求数据直接分析处理,降低了需求不确定性,这种方法下数据易获得、易更新,且计算方便简捷快速,可以为航空管理者参考,做出更为合理的舱位控制决策方案,提高航公司收益。此方法对航空收益管理研究中的舱位需求预测和舱位分配模型的优化改进是有益的补充,可以推广应用在高速铁路、快速汽车专线、定制旅游和定制酒店旅馆等行业,具有一定的专业意义和借鉴。

