基于衔接组合的集装箱多式联运服务分段采购优化

杨华龙，东方，刘迪

（1.大连海事大学交通运输管理学院，辽宁大连116026；2.广西民族大学商学院，南宁530006）

基于衔接组合的集装箱多式联运服务分段采购优化

杨华龙*1，东方2，刘迪1

（1.大连海事大学交通运输管理学院，辽宁大连116026；2.广西民族大学商学院，南宁530006）

为解决集装箱多式联运服务分段采购中的运输费用和运输时间优化难题，从多式联运经营人的视角出发，提出了集装箱多式联运总费用最小化和总运输时间最小化的双层优化目标.基于运输路径选择和时、空、量的衔接组合，结合托运人运单、集装箱多式联运组织形式、集装箱交接地点、运输路段及方式、运输时间、运费率等要素约束，建立了集装箱多式联运服务分段采购优化模型.运用自然约束语言设计搜索算法程序并求解.数值实验分析结果表明，该模型及搜索算法不仅易于实施求解，而且应用效果良好，达到了集装箱多式联运一体化无缝运输的目的.

综合交通运输;分段采购；衔接组合；集装箱多式联运；优化模型

1 引言

集装箱多式联运是指由两种或两种以上运输方式共同完成的集装箱运输，其服务交易过程极为复杂.多式联运经营人一方面要以承运人的身份为托运人提供集装箱运输服务，另一方面又以托运人的身份向水路、铁路、公路等实际承运人购买上述运输服务.如何采取一种集系统性和科学性于一体的方法，采购不同运输方式和不同运输路径下的优化组合运输服务，已成为集装箱多式联运经营人能否有效开展集装箱多式联运的一个难点.

目前，运输服务采购问题已受到许多学者的关注[1-3].在集装箱运输和多式联运服务采购领域中，Caris等[4]总结了多式联运决策研究主要是围绕政策支持、节点网络设计、联运服务网络设计、联运路径优化、运费操作和信息通信技术的创新等问题展开的.Chang等[5]以总运输成本和来自空气污染的外在成本最小为目标，建立了国际集装箱在韩国公路、铁路和近洋航线上的多式联运优化模型.Wang等[6]研究了集装箱多式联运系统中集装箱类型的选择和运输方式的组合优化，构建了模糊需求下运输成本最小化的数学模型，并利用改进的粒子-蚁群优化算法求解.蒋洋等[7]研究了寻求运输成本、转运费用等最小化的多式联运运输方案选择问题，并提出了交叉熵算法.王清斌等[8]研究了考虑集装箱多式联运在运输方式转换过程中节点作业随机特征的多式联运运输方式和路径选择模型.

综上，现有文献考虑的大多是从托运人的视角，以运费最小化为目标的运输服务采购优化问题.尚未充分考虑集装箱多式联运服务采购中的总费用最小化和总时间最小化的一体化无缝衔接双重目标问题，很少考虑到网络的可达性因素和运输网络的衔接问题，并不太适用于基于时间、地点衔接的集装箱多式联运分段运输服务采购问题.本文从集装箱多式联运经营人的视角上，以集装箱多式联运经营人向水/陆各路段实际承运人的运输服务进行分段采购为切入点，建立基于路径选择的集装箱多式联运服务分段采购优化模型，并基于自然约束语言设计相应的算法程序，以期丰富和完善集装箱多式联运运营组织理论和实践.

2 采购优化模型

2.1 问题描述

集装箱多式联运服务采购从总体上可以分为两个阶段，第一阶段是托运人向集装箱多式联运经营人进行运输服务采购，第二阶段则是多式联运经营人向水/陆各路段实际承运人进行运输服务的分段采购.从多式联运经营人的角度，向水/陆各路段实际承运人进行运输服务的分段采购优化问题可以描述为：假定有n个运单，要在规定的时间段内通过m个路段来完成（将相应的集装箱送达指定地点）.每个路段每天有若干个班次从起点行至终点，每个路段有其固定的运输方式、运输里程、运输时间、运输能力（标准集装箱）、运输费率.现需要多式联运经营人以总运输费用最小和总运输时间最小为目标，做出合理的运输安排，确定这n个运单的运输路径（路段组合）及运输时间，以便在规定的时间段内将其全部完成.

从集装箱多式联运供应链的角度来看，上述优化问题可以理解为多式联运经营人与多个水/陆各路段实际承运人合作，根据各路段的运力资源来规划各运单的运输路径、实际承运人，以及具体的运输时间，以使总运输费用最小和总运输时间最少.针对该问题中具体分段运输服务采购，集装箱多式联运经营人作为托运人，需要根据托运人运单中关于交接货物的地点和时间的要求，选择合适、合理的各路段运输方式，将其集装箱货物连贯地运输，通过多种运输方式的转换，最终到达目的地点.

多式联运经营人在选择多式联运的各路段服务时，既要考虑运输费用的因素，又要考虑总的时间效率因素.因此，双重优化目标分别为，多式联运所有路段的总运费最小和多式联运所有路段的总运输时间最少.

在集装箱多式联运服务采购优化问题中，主要有以下四方面的约束条件：

(1)空间约束：为运单选择的路径要满足，对于同一运单来说，它所经过的各路段的起点和终点必须首尾相接；运单的起点终点要与运输路径的起点终点相同.

(2)时间约束：优化问题的可行解不仅要满足时间窗口的约束，单个运单的运输也要满足时间先后顺序的约束.

(3)能力约束：每一路段班次上运输的所有运单要受到运输能力的约束，即处于每一路段的班次上运输运单的数量、重量之和必须小于该路段（班次）的最大运输能力.

(4)隐含约束：对于运单所含路段组合集合中的不同路段，其下一路段不能相同；在路段组合集合中，不同路段不能有相同的前一路段；相同路段上不同时间出发的班次上运输运单不能相同.

对于空间和时间链接的设计，本文引入了前后路段的变量，通过逻辑规划对前后路段的运输地点和交接时间做排序约束，前一路段的终点必须等于后一路段的起点，后一路段的开始运输时间必须晚于前一路段的到达时间.特别地，运单起始路段的起点应与运单发货地点相同，起始路段的发货时间应与运单发货时间相等，运单终止路段的终点应与运单交货地点相同，终止路段的交货时间应与运单交货时间相等，处于交货时间窗口内.

此外，为了使运单在终止路段的空间和时间上也能满足上述链接约束，需要作以下特殊处理：对于任意运单可增加一个虚拟的路段作为终止路段的后续路段，这样，运单的实际终止路段也存在后一路段，在地点和时间的衔接上也满足前后路段之间的所有空间和时间约束.运单增加的虚拟路段的起点与实际终止路段的终点相同，起运时间迟于实际终止路段上的到达时间，如图1所示.

2.2 模型构建

假设某集装箱多式联运经营人有n个运单，m个运输路段可供选择，每个路段j有kj个起运时间，运输费用为cj，最大装箱量为CQj，最大载重量为CWj，运输时间为tj.运单i的发运时间是从这m个运输路段的共∑j∈{1,m}kj个起运时间中选取的，其发货数量为qi，重量为wi，发货地点为Oi，接货地点为Di，要求集装箱货物到达目的地的时间满足时间窗[t1i，t2i]，t1i为运单i送达时间的下限，t2i为运单i送达时间的上限，k=∑j∈{1,m}kj为所有路段的起运时间之和.

在此多式联运各路段服务的采购问题中，运单i的路段数量未知，设为Li，显然Li≤m.运单i在起点的实际出发时间和到达终点的时间也是未知的，设为T1*i、T2*i，另外，由于路径不确定，运单i在其中间运输路段中的起点、终点、起运时间、到达时间都不确定，设其在第li(li∈{1,…,Li})个路段中的起点为S1i,li，终点为S2i,li，起运时间为T1i,li，到达时间为T2i,li，则该分段服务采购的优化模型可以描述如下：

目标函数

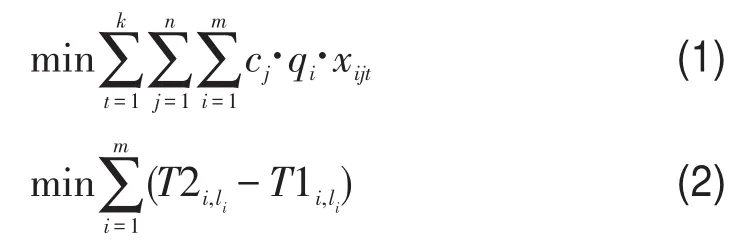
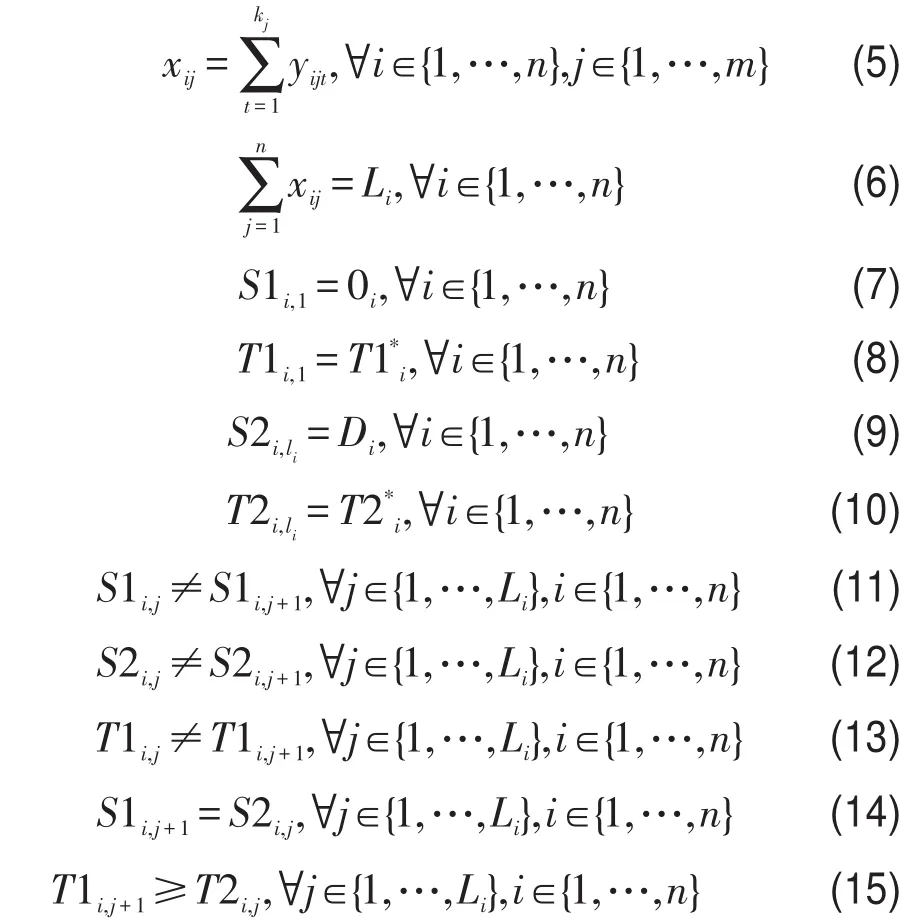
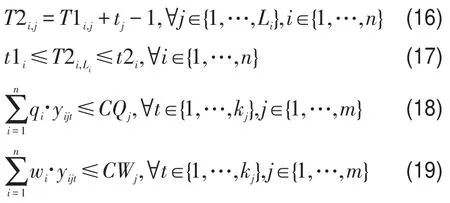
式(1)和式(2)为双重优化目标，分别表示多式联运所有路段的总运费最小和多式联运所有路段的总运输时间最少；

式(3)中，xij为0-1变量，表示运单i是否选择路段j；

式(4)中，yijt为0-1变量，表示运单i是否选择路段j的第t个起运时间；

式(5)定义了0-1变量xij和yijt之间的逻辑关系，表示如果运单i选择路段j，则运单i一定选择路段j的某一个起运时间kj，且此时的kj有且只有一个；

式(6)表示在集装箱多式联运中安排给运单i的路段数；

式(7)表示运单i的起始路段的起点与运单i的发货地点相同；

式(8)表示运单i在起始路段上的起运时间与运单i的发货时间相等；

式(9)表示运单i的终止路段的终点与运单i的交货地点相同；

式(10)表示运单i在终止路段上的到达时间与运单i的交货时间相等；

式(11)表示运单i的各个不同运输路段的起点不相同；

式(12)表示运单i的各个不同运输路段的终点不相同；

式(13)表示运单i的各个不同运输路段的起运时间不相同；

式(14)表示在运单i的各个运输路段中，前一路段的终点必须是后一路段的起点；

式(15)表示在运单i的各个运输路段中，前一路段的到达时间必须晚于后一路段的起运时间；

式(16)定义了运单i的任一路段上的到达时间，在数值上等于其在该路段上的起运时间加上运输时间再减去1；

式(17)约束了运单i在其终止路段上的到达时间必须满足时间窗要求；

式(18)表示每个路段任一时间运载的集装箱数量不能超过该路段自身的最大载箱能力；

式(19)表示每个路段任一时间运载的集装箱货物重量不能超过该路段自身的最大载重能力.

3 算法设计

通过上述分析和建模可知，集装箱多式联运服务分段采购优化模型不仅具有非线性的特点，还存在链接式排序问题.在对模型求解时，要用最短路问题求解的思路与空间、时间的链接问题相结合，形成所谓的“串”.而使用一般的求解软件很难描述地点和时间的链接，对于非线性问题的求解效率也不高.因此，需要调用人工智能逻辑进行搜索和求解.

本文使用自然约束语言（NCL）[9]，设计自然约束算法程序进行搜索和求解，步骤如图2所示.

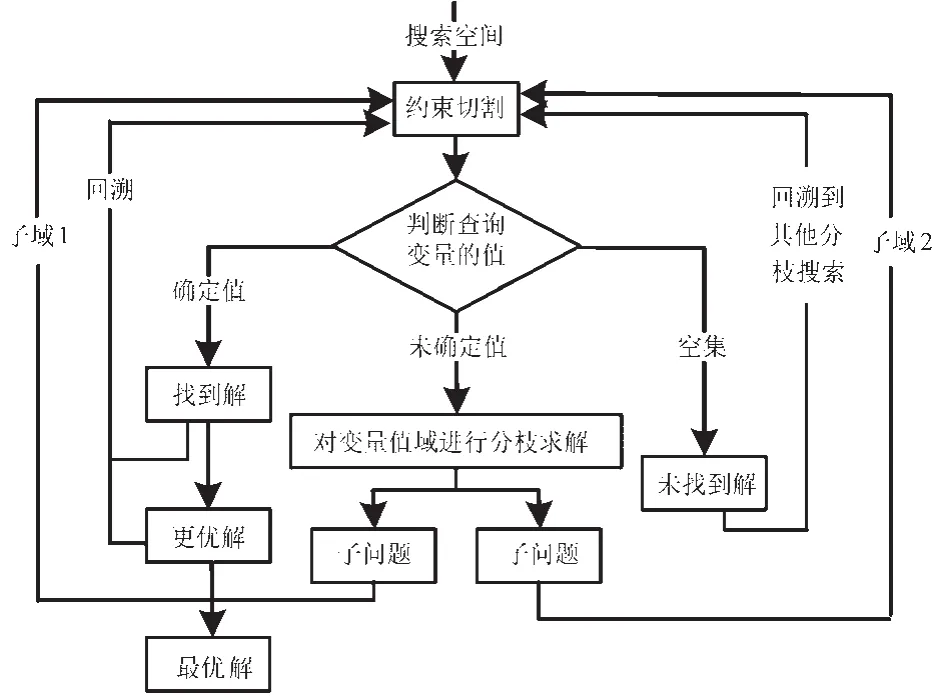
图2 求解步骤框架Fig.2 Framework of solving steps

优化模型中的0-1变量xij表示运单i是否选择路段j，在算法模型中使用集合变量RouteOrder表示，即将所有xij为1的承运人放入集合变量RouteOrder中.yijt则表示运单i选择路段j时间表中的第t个起运时间进行运输，由于时间选择的唯一性，因此算法模型中使用数值（非集合）变量shiftRouteOrder表示，设计基于混合集合规划的多式联运路径选择算法模型.

搜索策略1搜索具有瓶颈性质的变量运单终止路段lastRouteOrder.

按照如下顺序对非集合变量lastRouteOrder进行搜索：①集装箱数量较多的运单，②路段组合不确定性较小的运单，③各路段组合中可选终止路段较少的运单，④运单时间窗要求比较紧张的运单，⑤与运单的目的地点相同的路段，⑥运费较低的路段，⑦箱量总和较少的路段，⑧用时较少的路段，⑨里程数较小的路段，⑩各个路段的第一个起运时间，○11可使用班次数量较少的运单路段，○12实际使用的班次不确定性最小的路段.

搜索策略2搜索核心变量RouteOrder.

按照如下顺序对集合RouteOrder进行查询搜索：①运单路段组合不确定性最小的运单，②时间窗时间上限最小的运单，③集装箱数量较大的运单，④可以成为终止路段的路段，⑤运费率较低的路段，⑥路段的第一个发运时间，⑦装载集装箱数量之和较小的路段，⑧耗时较短的路段，⑨里程数较小的路段，⑩实际使用的班次不确定性最小的路段，○11可使用班次数量较少的运单路段.

搜索策略3搜索核心变量shiftRouteOrder.

按照如下顺序对非集合变量shiftRouteOrder进行查询搜索：①量较大的运单，②运输环节较少的运单，③运输顺序较小的运单路段，④遗憾度较小的运单，即最小遗憾度准则，选择值域的最大分枝进行搜索，⑤运单域非确定性较小的路段班次.

上述算法设计中使用的集装箱货物运单、路段、转运地点等信息数据，主要涉及到以下几类：

（1）托运人运单的相关数据.主要包括：运单号、运单下达时间、到达时间窗口、运输箱量、货物总重量、起始发货地点、最终到达地点.

（2）分段运输路段的相关数据.主要包括：路段编号、起点、终点、里程、运输时间、发车时间表、运输方式、承运人名称、运费率、班次最大载箱量、班次最大载重量.

4 数值实验分析

假设某集装箱多式联运经营人获得了30份托运人运单，结合现有运输网络中16个公路运输路段（A001-A016）、17个水运路段（B017-B033）和77个铁路运输路段（C034-C110）的里程、运输时间、承运人、运费率等信息，利用本文构建的优化模型和自然约束算法程序进行搜索和求解，得到托运人运单和运输路径甘特图，如图3、图4所示.

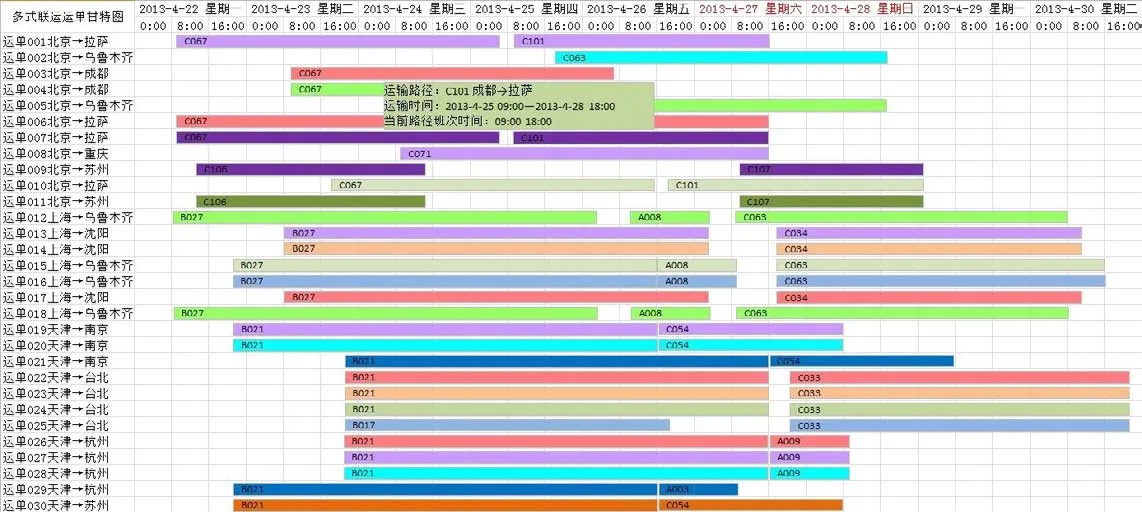
图3 运单甘特图Fig.3 Gantt chart of waybill

图4 运输路径甘特图Fig.4 Gantt chart of transportation route

从图3和图4中可以看出，集装箱多式联运经营人对分段运输服务的采购进行了有效的组合优化，将运单集中安排在从2013-04-22到2013-04-26共五天时间内，对分段运输服务的采购计划做出了组合优化上的分配，不仅实现了总运输费用的最小化，而且运力安排紧凑，实现了时间上的优化.一共需要采购59个分段运输计划，组合以后共有15条运输路径，运单的运输需求全部满足，在2013年4月22日-4月30日期间内运输任务全部完成，达到集装箱多式联运一体化无缝运输的目的.

5 研究结论

本文的主要工作在于从多式联运经营人的角度出发，基于运输路径选择和时、空、量的衔接组合，结合托运人运单、集装箱多式联运组织形式、集装箱交接地点、运输路段及方式、运输时间、运费率等要素，建立了集装箱多式联运服务分段采购组合优化模型.运用NCL语言设计自然约束模型并进行搜索和求解.算例分析结果显示了该模型及算法的有效性.对比以往研究运输服务采购的相关文献，本文突破了传统研究只考虑单一运输服务采购的界限，同时充分考虑集装箱多式联运服务采购中的费用最小化和总时间最小化的一体化无缝衔接双重目标问题，进而丰富和完善了集装箱多式联运运营组织理论和实践.下一步的研究可以从集装箱多式联运经营人和托运人双方合作共赢的角度展开，将集装箱多式联运服务采购的两个阶段相结合，即将托运人向集装箱多式联运经营人进行运输服务采购的第一阶段与多式联运经营人向水/陆各路段实际承运人进行运输服务分段采购的第二阶段整合集成.

[1]Lim A,Rodrigues B,Zhou X.Transportation procurement with seasonally varying shipper demand and volume guar⁃antees[J].Operations Research,2008,56(3):758-771.

[2]Rekik M,Mellouli S.Reputation-based winner determi⁃nation problem for combinatorial transportation procure⁃ment auctions[J].Journal of the Operational Research Society,2012,63(10):1400-1409.

[3]Huang G Q,Xu S X.Truthful multi-unit transportation procurement auctions for logistics e-marketplaces[J]. Transportation Research Part B-methodological,2013, 47:127-148.

[4]Caris A,Macharis C,Janssens G K.Decision support in intermodal transport:A new research agenda[J].Com⁃puters in Industry,2013,64(2):105-112.

[5]Chang Y T,Lee P T W,Kim H J,et al.Optimization model for transportation of container cargoes consider⁃ing short sea shipping and external cost[J].Transporta⁃tion Research Record:Journal of the Transportation Re⁃search Board,2010,2166:99-108.

[6]Wang H,Wang C X.Selection of container types and transport modes for container multi-modal transport with fuzzy demand[J].Journal of Highway and Transportation Research and Development,2012,29(4):153-158.

[7]蒋洋,张星臣,王永亮.多式联运运输方案选择的交叉熵方法[J].交通运输系统工程与信息,2012,12(5):20-25. [JIANG Y,ZHANG X C,WANG Y L.A cross-entropy method for solving selection of multimodal transportation scheme[J].Journal of Transportation Systems Engineer⁃ing andInformation Technology,2012,12(5):20-25.]

[8]王清斌,韩增霞,计明军,等.基于节点作业随机特征的集装箱多式联运路径优化[J].交通运输系统工程与信息,2011,11(6):137-144.[WANG Q B,HAN Z X,JI M J,et al.Path optimization of container multimodal transportation based on node operation randomness[J]. Journal of Transportation Systems Engineering and Infor⁃mation Technology,2011,11(6):137-144.]

[9]周建阳.自然约束语言[M].北京：科学出版社，2009年.[ZHOU J Y.Natural constraint language[M].Beijing: Science Press,2009.]

Segmented Procurement Optimization of Container Multimodal Transport Service Based on Convergent Combination

YANG Hua-long1,DONG Fang2,LIU Di1
(1.Transportation Management College,Dalian Maritime University,Dalian 116026,Liaoning,China；2.Business School,Guangxi University for Nationalities,Nanning 530006,China)

ract:To solve the transport cost and time optimization problem in segmented procurement of container multimodal transport service,this paper proposed the double optimization objectives including minimization of total transport cost and total transport time in container multimodal transport from the perspective of multimodal transport operators.Based on the routes selection and convergent combination of transport time, space and volume,the paper developed an optimization model of segmented procurement in container multimodal transport with regard to the elements constraints of shippers’orders,organization forms of container multimodal transport,container delivery location,transportation section and mode,transportation time and freight rate.The Natural Constraint Language was employed to establish a searching algorithm procedure for solving the problem.Numerical examples show that the model and its searching algorithm not only can be implemented easily to solve the problem,but also the application results are quite well and the goal of seamless integrated container multimodal transport is achieved.

rds:integrated transportation;segmented procurement;convergent combination;container multimodal transport;optimization model

1009-6744（2014）04-0017-06

U169

A

2013-11-19

2014-01-19录用日期：2014-02-19

国家自然科学基金(71372088,70972008)；辽宁省教育厅科学研究项目（L2013207）；大连市科技计划项目(20120275)；中央高校基本科研业务费资助暨大连海事大学优秀科技创新团队培育计划资助项目（2011ZD027）.

杨华龙(1964-)，男，辽宁庄河人，教授、博士生导师. *

hlyang@dlmu.edu.cn