基于风险分担的城市公交出行鲁棒优化模型

章宇，唐加福*,2

（1东北大学流程工业综合自动化国家重点实验室，沈阳110004；2东北财经大学管理科学与工程学院，辽宁大连116000）

基于风险分担的城市公交出行鲁棒优化模型

章宇1，唐加福*1,2

（1东北大学流程工业综合自动化国家重点实验室，沈阳110004；2东北财经大学管理科学与工程学院，辽宁大连116000）

本文面向城市中需要在给定期限内到达终点的出行者，针对最短耗时公交换乘问题，利用基于风险分担的鲁棒优化方法进行了建模和求解.公交行车时间和发车间隔时间是不确定的，本文将其建模为区间数，并基于风险分担的思想给出了这些不确定参数的集合描述，该集合可以通过一个代表出行者保守程度的参数进行灵活调整，在此基础上提出了城市公交换乘最短耗时鲁棒优化模型，给出了多项式时间精确算法.通过对一个算例的求解和仿真实验，展示了该模型求解结果（相对于确定性模型的求解结果）具有更小的迟到概率；并通过分析讨论，总结出换乘更少，运行更稳定的换乘方案更倾向于成为鲁棒最优换乘方案.

城市交通；换乘路径优化；鲁棒优化；公交出行者；风险分担

1 引言

城市中公交出行者在出行前往往需要制定一套公交换乘方案，使得出行消耗的总时间最短.现实生活中，某些出行者必须在规定的最后期限前到达出行终点（如去开会、赴约、参加面试、赶火车、上班等）.如果公交车的行车时间和乘客的换乘等车时间是确定的，公交换乘问题很容易求解，此前已有大量的相关研究.公交换乘问题往往被视为变种的最短路问题，用改进的最短路算法即可求解.例如，樊晓春等人借助公交网络通达矩阵利用改进的Dijkstra算法进行求解[1]；Zografos和Androutsopoulos用一种动态规划方法进行求解[2].但这些研究都假设公交行车时间及换乘等待时间是确定的，运用求解得到的换乘方案出行很可能导致出行者的迟到.

事实上，公交行车时间及乘客等车时间是不确定的，同时它们相应的分布函数也不可能准确地获取，这就给公交出行换乘方案的制定带来了困难和挑战.现实中，具有到达终点最后期限限制的出行者往往宁愿牺牲一些时间“提前”出发，使得对于绝大多数的不确定情况都不迟到，也不愿冒险“准点”到达；此外，“提前”量不是无限的，出行者希望定量地知道什么时刻出发.

近年来，鲁棒优化方法论逐渐兴起并得到了广泛运用，它本质上是一种“保守”的方法，所以正好适用于该问题.一些学者利用最小化最大遗憾准则对鲁棒最短路问题进行建模和求解，导致该问题变为NP难题，故不适用于现实场景[3-6].而针对鲁棒最短路问题，Bertsimas和Sim基于风险分担的思想，考虑弧段车辆行驶时间为区间数，但只有给定个数的弧段消耗的时间能够达到最坏值（却没给定哪些弧段），在这样的前提下要求寻求最坏情况下的最短路径；该模型可以在多项式时间内求解，因此更具有实用性[7].

本文借鉴Bertsimas和Sim的方法，面向公交出行者，针对城市公交换乘问题，考虑公交行车时间及发车间隔时间的不确定性，以出行耗时最少为目标，提出基于风险分担的鲁棒优化模型.给出公交行车时间和出行者换乘等待时间的不确定集合描述，以及多项式时间求解算法.并通过一个算例仿真地验证了该模型的有效性，揭示了对于具有最后期限限制的公交出行者，一套鲁棒换乘方案并不是“在确定性模型所求得的最优方案基础上提前一些时间出发”那么简单.同时总结出对于偏好保守的出行者，即使出行距离相对更大，也要选择换乘更少，运行更稳定的换乘方案.本文不仅对鲁棒优化方法论在公交换乘优化领域的应用具有理论推动意义，而且对乘客公交出行安排具有管理学上的实际指导意义；此外，该模型可以作为子模型嵌套到公交网络流分配模型和公交线路设计模型中，具有广泛的应用潜力.

2 公交网络描述

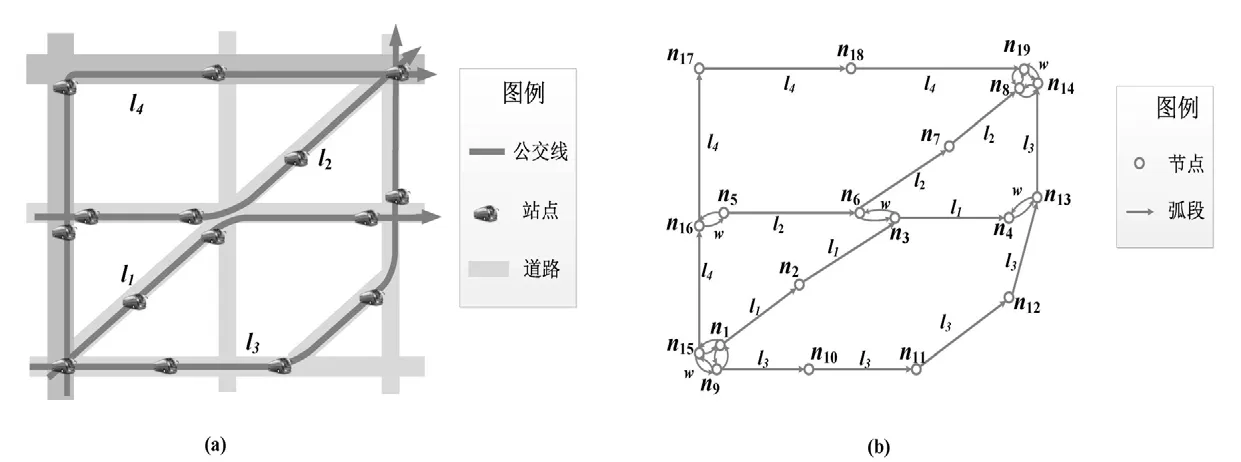
图1 城市公交网络模型示意图Fig.1 An urban bus network sample

图1(a)和(b)分别展示了城市公交网络物理结构和对应的网络模型，下面进行详述.

Aw：换乘弧段集，包括步行和等车两个过程，两节点间步行距离须小于某一给定阈值.

出行者每一次出行会给定起点no∉N和终点nd∉N，不失一般性地认为它们不正好在之前定义的节点上.则每当给定起始点时，需在原网络G中添加换乘弧段连接起点与终点.并令hl(no)=hl(nd)=hˆl(no)=hˆl(nd)=0.

3 公交换乘鲁棒优化模型

出行者欲制定一套换乘方案使得出行时间最短且尽量不迟到.欲确定最晚的出发时刻，可等价地最小化换乘方案总出行时间.本文假设：①公交车容量是无限的；②乘客出行期间各线路皆未停运；③站点间公交行车时间的不确定区间数能准确获取.那么，不确定环境下城市公交换乘优化模型可表示为目标式(3)以及约束式(4)～式(6).如目标式(3)所示，出行者以出行总耗时最短为目标；决策变量为当弧在最优换乘方案上时否则则决策变量为0-1变量，如约束式(6)所示；约束式(4)保证所选择的弧形成一条起始点间连通的路；两条换乘弧段不能直接相连，如约束式(5)所示.

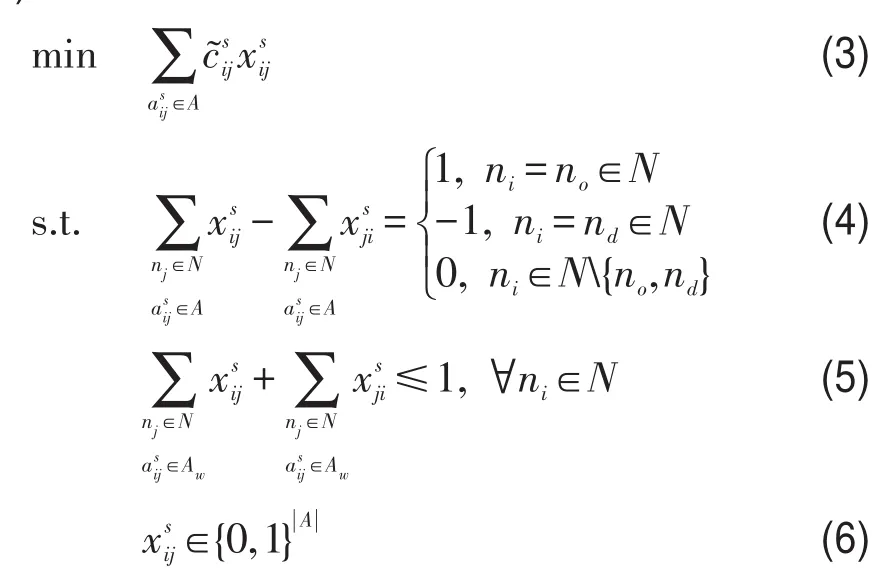
如果参数c～isj取其标称值cisj，则该问题不考虑不确定性，称之为标称问题.它是最短路问题的一个变种，简单修改Dijkstra算法即可在多项式时间内高效求解.但其计算结果很可能导致迟到，所以必须考虑不确定性.

如每个参数c～isj同时取到对应的最大值，将导致出行者提前太长时间出发，这样的求解结果不能令人满意.本文则借鉴Bertsimas和Sim的想法[7]，提出城市公交换乘鲁棒优化模型，设计目标函数式(7)，满足约束式(4)～式(6)及式(8)～式(9).其中，zisj为辅助变量，Γ={0,1,...,|A|}为控制保守 程度的参数，由出行者决定.如果 Γ=0，出行者很乐观，但理论上有50%的概率会迟到，问题退化为前述标称问题；如果 Γ=|A|，出行者很悲观，他不会迟到，但很可能提前太长时间到达目的地；Γ参数的设定正是根据出行者的保守程度，在可能迟到和提前太长时间到达目的地之间取一个折中.

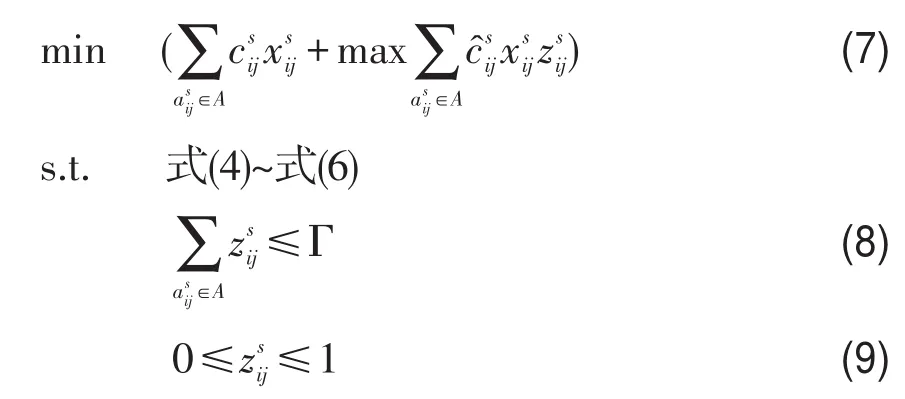
4 多项式时间精确算法

由于弧段消耗的时间为不确定值，Dijkstra算法不能求解.本节给出上述模型的多项式时间精确解法.

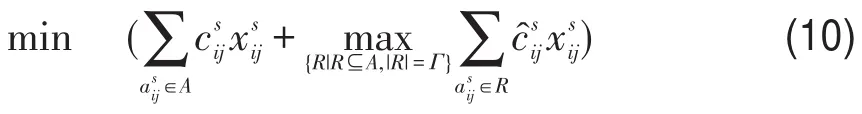
定理约束式(8)、式(9)连同目标式(7)等价于目标式(10).证明：观察目标函数式(7)，它对于变量线性，且式(8)中Γ为整数，则结合式(9)可知只在端点0或1处取得最优值；同时，通过反证法可证目标函数中的使得约束式(8)等价于因为如果总可增大使增大.证毕.

目标式(10)可直观理解为网络G中虽弧的耗时值是不确定的，但仅有Γ条弧会实现其最长耗时值，其它保持为标称值.本模型事实上是从风险分担的角度出发的，也就是说，真正耗时值比相应标称值大的弧段可能很多（如＞Γ），但不都会实现其最大偏离值，本模型则以Γ条弧耗时最大偏离值之和来代表，从而分担了风险.

证明：根据Bertsimas和Sim的论文[7]，可得到该性质.

根据该性质，欲求解上述鲁棒优化问题，可等价地求解|A|+1个确定性问题，再取最小值.每一个确定性问题是一个变种的最短路问题，可利用算法复杂度为O(n2)的Dijkstra算法求解.这样，该不确定性问题就可等价地由最初穷举式的求解个确定性问题变为求解最多|A|+1个确定性问题.相应地，求解算法也从非多项式时间缩减为多项式时间O((||A+1)n2).

本文默认读者熟悉Dijkstra算法，基于以上性质，下面给出求解该问题的算法步骤：

步骤1对于k=1,2,...,||A+1，分别利用Dijkstra算法求解目标式(12)满足约束式(4)～式(6)的优化问题，令Gk问题对应的最优解为向量xk.

步骤2求

步骤3最优目标函数值最优解

5 算例求解与分析

图2为一个不确定环境下公交网络示例，其物理结构如图1(a)所示.出行者设置起点为n20，终点为n21.他欲到终点见客户，故希望获得一套鲁棒的公交换乘方案.

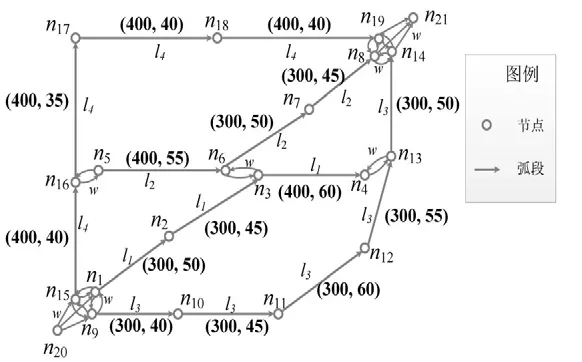
图2 不确定环境下公交网络示例Fig.2 A bus network example under uncertainty

每条公交弧段对应括号中的两个数中，第一个为通过该弧的期望耗时，第二个为最大偏差耗时，单位为s.线路1～4的期望发车间隔分别为480，360，360，300 s；最大偏差值分别为100，90，90，60 s.节点n1,n9,n15,n20两两间的距离均为0，因为它们在地理上是同一地点，只是被建模为多个节点；节点n8,n14,n19,n21同理两两间距离为0；节点对n5与n16，n3与n6，n4与n13间步行距离均为30 m，步行速度设定为1.5 m/s，则耗时均为20 s.

利用第4节所述方法对上述算例进行求解.随机生成1 000个Γ∈{1,2,...,|A|}，其平均求解时间为标称模型求解时间的8.64倍，与该算例对应的理论值9倍（可由上述性质计算）基本吻合.

对于Γ=0,1,...,|A|分别对该算例进行求解.计算可得，当Γ=0时最优换乘方案为出行耗时1640 s；Γ=1时，最优换乘方案为，耗时1950 s；Γ≥3时，最优换乘方案为当2 040，2 080，2 115 s.

此外，关心在给定不同的提前于最后期限出发时间的情况下，上述三套换乘方案究竟有多大的概率导致出行者迟到.假设所有的公交弧耗时和发车间隔时间均匀分布在给定区间，随机取10 000个场景，对于每个场景分别计算三种换乘方案的时间消耗，则统计可得迟到概率如表1所示.

表1 不同换乘方案及不同的提前于最后期限出发的时间所对应的迟到概率（单位：%）Table 1 late probabilities for different itineraries combined with different advanced departure time(in seconds)

对于以上结果，讨论如下：

(1)虽然出行者提前最后期限于1 640 s出发时，p1迟到概率小于p3，但仍然有约50%的迟到概率，出行者显然会提前更多的时间出发，而当出行者至少提前2 040 s出发时，选择p3基本上可保证不迟到.所以，一套鲁棒换乘方案并不是“在标称模型所求得的最优方案基础上提前一些时间出发即可”那么简单.另外，本文定量地计算出需要多“早”出发.

(2)Γ=0即不考虑不确定性时，最优方案为p1，这主要得益于该方案空间距离最短.但随着Γ逐渐增大，p2和p3依次成为最优换乘方案，这是因为p1比p2和p3多一次换乘，而一次换乘等待时间的不确定性远大于一条公交弧段耗时的不确定性.所以保守的出行者应该尽量少换乘，即使行驶距离更长.

(3)Γ=1时最优换乘方案为p2，这主要得益于其空间距离比p3短.而同样的换乘次数，当Γ≥2时，p3却优于p2，这是因为p3对应的公交线路行车时间的最大偏离值较小.所以保守的出行者应该尽量选择稳定性高的换乘方案，即使行驶距离更长.

6 研究结论

对于城市公交出行者需要在给定期限内到达终点的情况，如果按照传统的标称问题求解，其结果很可能导致出行者迟到；寻找一套鲁棒换乘方案也并不是“在标称模型所求得的最优方案基础上提前一些时间出发即可”那么简单.本文将不确定的公交行车时间和发车间隔时间给定为区间数，但是只有限定个数的参数能同时到达最坏值，随后给出了城市公交换乘鲁棒优化模型与多项式时间精确算法.通过对一个算例的求解和仿真分析展示了该模型的正确性和实用性，给出了求解结果的置信度，总结出换乘少和运行稳定的换乘方案更具有抗干扰的能力.

[1]樊晓春,张雪英,刘学军,等.一种公交换乘优化算法设计[J].地球信息科学学报,2009,11(2):157-160. [FAN X C,ZGANG X Y,LIU X J,et al.Design of an algo⁃rithm of public traffic transfer based on the least transfer [J].Geo-Information Science，2009,11(2):157-160.]

[2]Zografos K G,Androutsopoulos K N.Algorithms for itin⁃erary planning in multimodal transportation networks[J]. Intelligent Transportation Systems,IEEE Transactions on,2008,9(1):175-184.

[3]Yu G,Yang J.On the robust shortest path problem[J]. Computers&Operations Research,1998,25(6):457-468.

[4]Montemanni R,Gambardella L M.An exact algorithm for the robust shortest path problem with interval data [J].Computers&Operations Research,2004,31(10): 1667-1680.

[5]Catanzaro D,Labbé M,Salazar-Neumann M.Reduction approaches for robust shortest path problems[J].Comput⁃ers&Operations Rresearch,2011,38(11):1610-1619.

[6]Gabrel V,Murat C,Wu L.New models for the robust shortest path problem:complexity,resolution and gener⁃alization[M].Annals of Operations Research,2011:1-24.

[7]Bertsimas D,Sim M.Robust discrete optimization and network flows[J].Mathematical Programming,2003,98 (1-3):49-71.

A Risk-Pooling-Based Robust Model for Least-Time Itinerary Planning

ZNANG Yu1，TANG Jia-fu1,2
（1 State Key Lab of SyntheticAutomation of Process Industries,Northeastern University,Shenyang 110004 China;2 College of Management Science and Engineering,Dongbei University of Finance and Economics,Dalian 116025,Liaoning,China）

ract:This paper addresses the least-time itinerary planning problem for the urban public-transport travelers,especially those with deadlines imposed at their destinations.A risk-pooling-based robust model is used to solve the problem.Headway and travel time of each bus are uncertain,which are given in intervals in this paper.Based on the risk pooling concept,the set of combined uncertain travel times and headways are designated.This set could be adjusted flexibly by a parameter,which represents the conservativeness of each traveler.Subsequently,a robust model for the problem is proposed,as well as an exact polynomial time algorithm.Through an example and the associated simulation,the paper demonstrates that the solution of this model(compared with the solution of the deterministic model)is less likely to break the deadline.It is also concluded that an itinerary is more inclined to be a robust optimal solution with less transfer times or by more reliable bus lines.

rds:urban traffic;itinerary planning;robust optimization;bus traveler;risk pooling

1009-6744（2014）04-0107-00

U268.6

A

2013-12-12

2014-04-01录用日期：2014-04-11

国家创新研究群体科学基金（71021061）.

章宇（1989-），男，四川内江人，博士生. *

tangjiafu@dufe.edu.cn