有偏好的多属性灰色关联路径选择模型

郑建湖，伍雄斌，黄明芳，文子娟

（闽江学院交通学院，福州350108）

有偏好的多属性灰色关联路径选择模型

郑建湖＊，伍雄斌，黄明芳，文子娟

（闽江学院交通学院，福州350108）

路径选择模型是动态交通诱导的核心问题.针对出行者不同偏好及路径属性不完全确定条件下，提出了一种路径属性为区间值的有偏好路径选择模型.建立了以交通拥挤程度、行程时间、行程距离和行程时间可靠性为属性的路径选择指标体系，给定路径属性的区间值及出行者偏好值，计算每条路径客观信息与主观偏好的灰色关联系数.为了减少主观偏好与客观信息的偏差，构建了单目标最优化模型，得到路径属性的权重值，进而求得各路径主观偏好与客观信息的关联度，并根据关联度大小进行排序.最后以福州三坊七巷交通网络为例，给出路径选择实例.结果表明该方法简单有效.

智能交通；路径选择；灰色关联分析法；多属性决策；出行者偏好

1 引言

路径选择行为建模一直是交通管理领域的研究热点问题之一，更是动态路径诱导的核心问题.如何在交通网络的众多有效路径中，找出一条符合出行者意愿的“最优路径”，使出行者顺利地从起点到达终点，是路径选择行为建模的关键.传统的路径诱导一般只考虑行程距离或行程时间等某一指标，这与实际出行者路径选择行为不符.因为出行者在路径选择时考虑的因素众多，不同的出行者考虑的因素也不尽相同，主要受出行目的、个人喜好等出行者主观因素及路径行程时间、交通拥挤程度、行程距离等客观信息的影响.因此，路径选择行为是一种基于出行者偏好的多属性决策行为.

针对多属性路径选择行为，国内外学者进行了大量的研究工作，并取得一些富有成效的研究成果.文献[1]对路径选择模型作了全面的回顾及展望，同时指出路径选择模型在交通管理中的重要性.Lam等考虑了出发时刻、路径长度、停车位置、停车时长等多个因素对出行者路径选择行为的影响，建立了变分不等式路径选择模型，并利用遗传算法进行求解[2].Opasanon等假设路径各属性为离散的随机变量，提出了一个基于随机优势产生所有Pareto最优解的路径选择算法[3].Turan Arslan等以旅行时间、交通拥挤程度、安全性等路径属性，提出了一种基于AHP与模糊逻辑相结合的混合路径选择行为分析方法[4].Sitarz将路径多属性通过综合加权的方法合并为单属性，利用蚁群算法进行求解[5].Chen等建立多属性条件下的路径选择模型,并用蚁群算法进行求解[6].Gao等提出了路径选择策略的一个基本体系，并将涉及的各个属性变量进行分类，建立了一个具体的路径选择算法，但算法复杂性是指数型的[7].以上讨论的多属性路径选择模型均未考虑出行者的个人偏好，由于路径选择影响因素众多，出行者在出行过程中，往往会根据个人的喜好与习惯做出主观判断，选择符合个人意愿的出行路径.

目前，关于有偏好出行路径选择行为的研究成果较为少见.孙燕等以路径行驶时间、行驶距离、沿途景观等属性建立了基于灰色系统理论的最优路径选择方法，并分析了驾驶员不同偏好对路径选择结果的影响[8].陈京荣等建立了一个有偏好的交通网络路径选择模型，并分析了有、无偏好对路径选择行为的影响[9].由于实际的交通网络是动态变化的，系统给出各条路径属性值时往往只是某一区间值，而不同的出行者考虑的影响因素也不同，因此路径各属性的权重信息也不完全确定.本文在这些条件下，对有偏好的多属性路径选择问题进一步拓展，对路径各属性值为区间数，属性权重值也为区间数的情况下，利用灰色关联分析法,求得出行者主观偏好与路径客观信息之间的关联度，进而进行路径选择.

2 路径选择指标体系

综观以往的研究，影响出行者路径选择的因素可分为两大类：一类是出行者的主观因素，主要包括出行者的个人出行经验、个人出行喜好、个人经济水平等因素；另一类是路径的客观因素，主要有路径的行程距离、路径行程时间、路径交通拥挤程度、交叉口数量、沿途景观等.虽然影响出行者路径选择的影响因素众多，但路径选择行为的目标是一致的，通常都是以自己期望的最小费用为目的选择行使路径，但不同的出行者有不同的偏好，对路径属性值有不同的判断标准和心里接受范围.一般来说，早期道路交通畅通的时候，人们通常以行程距离或行程时间最小为性能指标来选择最佳路径.随着城市交通拥挤的日益严重，人们也常把交通拥挤程度作为路径选择的一个重要因素，因为它影响到出行者的舒适性和安全性.但由于交通系统的复杂性和不确定性，交通网络中路径的行程时间也是动态变化的，不同出行目的考虑的因素也不一样.Liu H X等研究表明，行程时间可靠性也是影响出行者路径选择的一个重要因素[10].大量的研究表明，行程时间可靠性是驾驶员路径选择的关键，驾驶员并不希望选择行程时间短但波动性大的路径，因为人们总是希望能在规定时间内到达目的地.因此本文选取行程时间、行程距离、交通拥挤程度、行程时间可靠性作为路径选择评价指标，能较好地反映出行者在实际出行中考虑的关键因素.

3 路径选择模型的建立

记某一交通网络为G=(V(G),E(G)),其中V(G)为网络的交叉口集，E(G)为网络的路段集.给定起点O到终点D有m条可行路径出行者选择某条路径是由路径的n个属性决定的，每个属性的属性值为区间数则原始决策矩阵为

为了消除不同量纲对出行路径选择决策的影响，对原始决策矩阵进行规范化处理[11]，把路径各属性值统一变换到[0，1]范围内.

对于效益型属性：

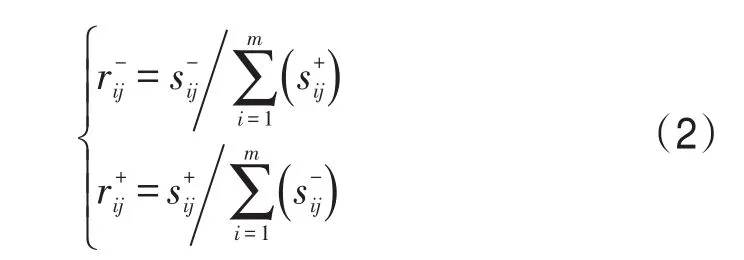
对于成本型属性：

规范处理后的决策矩阵记为

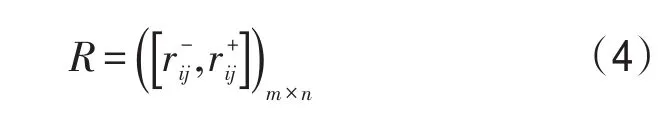
式中i=1，2，…，m，j=1，2，…，n，规范后的决策矩阵中的属性值表示出行者对路径选择的客观信息值.

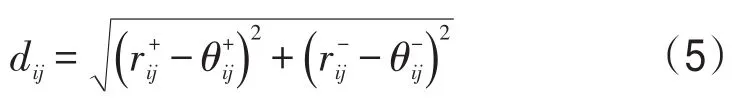
则出行者主观偏好值与客观偏好值的灰色关联系数ξij为[13]

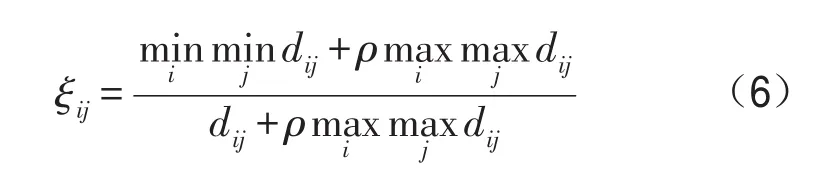
式中ρ为分辨系数，它有助于提高关联系数之间的差异显著性，一般取ρ=0.5效果较好.

由于出行者选择路径的影响因素众多，为了减少出行者的主观偏好与客观信息之间存在的偏差，路径属性权重向量w=() w1，w2，…，wn应使出行者的主观偏好与客观信息之间的偏差最小，为此建立如下单目标最优化模型：

根据式（7）最优化模型，求得路径各属性权重，进而计算各条路径客观信息对主观偏好的关联度ξi.关联度越大，表明出行者的主观偏好与路径客观信息越接近，从而该条路径越优.

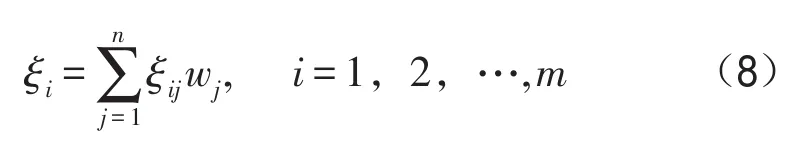
综上所述，区间数多属性条件下路径选择问题的计算步骤可归纳如下：

Step 1利用式（2）和式（3）对原始决策矩阵进行规范化处理；

Step 2依据出行者对各条路径的主观偏好，计算路径各属性值的客观信息与出行者主观偏好之间的区间数欧式距离dij；

Step 3依据式（6）求出行者主观偏好值与客观信息值的灰色关联系数ξij；

Step 4建立单目标最优化模型，使出行者的主观偏好与客观信息之间的偏差最小，从而求得路径各属性权重wj；

Step 5依据式（8）求各路径客观信息与主观偏好的关联度，并根据关联度大小进行排序，关联度越大表示该路径越优.

4 实例分析

本文选用福州市三坊七巷的区域交通网络作为实例，如图1所示.假设出行者从起点O到终点D，共有三条可选路径，即路径A：1→2→6→7；路径B:1→3→4→7；路径C：1→3→4→5→6→7.

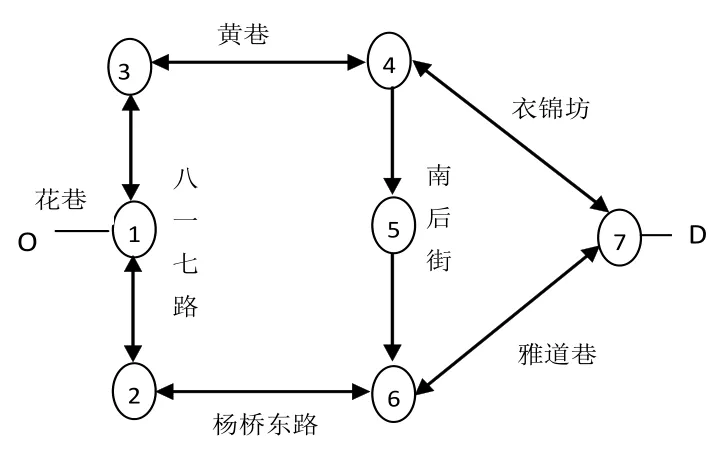
图1 交通网络Fig.1 Traffic network

由于不同出行者对路径各个属性指标值的感受不同，因此各个属性均采用区间数的表示方法，采用0-9表示出行者对路径各属性的赋值，从0-9表示各属性指标值从小到大，如交通拥挤程度为0表示最不拥挤，9表示交通拥挤最严重，其余类似.通过咨询有该区域出行经验的专家和随机调查三坊七巷周边道路的驾驶员，得到每个出行者给出的路径各属性的区间数，经平均处理后得出该交通网络各路径属性的原始区间数如表1所示.假设路径各属性的权重也为区间数：

并给定出行者对各条路径的主观偏好值为

在这个多属性路径决策中，属性类型分为成本型和效益型两类，其中交通拥挤程度A1,行程时间A2、行程距离A3为成本型属性，行程时间可靠性A4为效益型属性.规范化后的决策矩阵为

表1 路径各属性区间数Table 1 Interval value of each attribute

则路径各属性的客观信息与主观偏好之间的区间数欧式距离为

由式（6）计算各条路径客观信息对于主观偏好值的灰色关联系数为

由式（7）得到单目标最优化模型为解得路径各属性权重向量w=() 0.24,0.29,0.23,0.24.

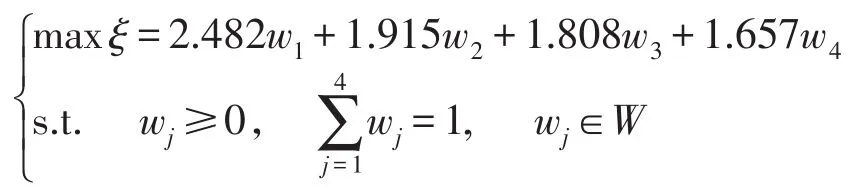
由式（8）求得各路径主观偏好与客观偏好的关联度 ξA=0.6950，ξB=0.7968，ξC=0.4727.

由此按照 ξi值的大小得到出行者对各路径选择的优先排序，即B≥A≥C，因此路径B最优.

由于路径各属性的指标值来自比较熟悉该区域交通网络的出行者，具有该区域交通网络的出行经验，其给出的路径属性值能较好地反映该路网的实际情况.这一实例路网处于福州市中心，东临八一七北路，西靠通湖路，北接杨桥路，南达吉庇巷、光禄坊，车流量相对密集，交通较易产生拥挤.利用本文所提出的多属性灰色关联路径选择模型，对福州三坊七巷的区域交通网络进行实证研究.三条路径的排序与实际情况是比较相符的，路径A虽然道路较宽，但距离较路径B长一些，且交叉口信号周期较长，而路径B虽然比路径A拥挤一些，但行程距离、行程时间比路径A短，行程时间可靠性比路径A好，因此路径B为最优路径，符合此路网实际情况.

5研究结论

在智能交通系统(ITS)得到广泛应用的城市交通中，出行者路径选择问题无疑是研究的热点与难点，最佳的路径选择有益于缩短出行者的行程时间，同时对城市交通拥挤也起到一定的缓解作用.针对路径选择问题的多属性特点，根据出行者路径选择影响因素的模糊性与不确定性，本文在路径属性值与权重值均为区间数的情况下，提出了一种基于灰色关联分析法的有偏好多属性路径选择模型.并以福州市三坊七巷的实际路网为例，采用专家打分的方法对路径各属性及权重赋值，利用本文提出的多属性路径选择模型进行实例分析，结果与实际交通情况相符.该方法提供的最优路径选择排序，为出行者快捷地到达目的地提供决策依据，从而为城市交通的智能导航提供了一些借鉴思路，但是交通网络是一个复杂的巨系统，

路径信息也是动态变化的.出行者的路径选择行为与路网的实时交通状态相互影响，路径选择行为影响着路网的交通流量，路网的交通流量又影响着驾驶员的路径选择行为，不同的出行目的考虑的因素也不尽相同，因此如何在不确定信息下为出行者提供及时高效的路径诱导还需进一步的研究.

[1]Carlo Giacomo Prato.Route choice modeling:past,pres⁃ent and future research directions[J].Journal of Choice Modeling,2009,2(1):65-100.

[2]Lam W H K,Li Zhichun,Huang Haijun,et al.Modeling time-dependent travel choice problems in road net⁃works with multiple user classes and multiple parking fa⁃cilities[J].Transportation Research Part B,2006,40(5): 368-395.

[3]Opasanon S,Miller-Hooks E.Multi-criteria adaptive paths in stochastic,time-varying networks[J].European Journal of Operational Research,2006,173:69-73.

[4]Turan Arslan C，Jotin Khisty.A rational approach to handling fuzzy perceptions in route choice[J].European Journal of Operational Research,2006,168:571-583.

[5]Sitarz S.Ant algorithms and simulated annealing for multi-criteria dynamic programming[J].Computer&Op⁃erations Research,2009,36:433-441.

[6]陈京荣,俞建宁,李引珍.基于蚁群算法的多属性路径选择模型[J].系统工程,2009,27(5):30-34.[CHEN J R,YU J N,LI Y Z.Model of choosing routes with multi-attributes based on colony algorithm[J].Systems Engineering,2009,27(5):30-34.]

[7]Gao Song,Chabini.Optimal routing policy problems in stochastic time-dependent networks[J].Transportation Research Part B,2006,40(2):93-122.

[8]孙燕,陈森发,亓霞,等.基于灰色系统理论的最优路径选择方法[J].土木工程学报,2003,36(1):94-98. [SUN Y,CHEN S F,QI X,et al.Optimal route selection method based on gray system theory[J].China Civil Engi⁃neering Journal,2003,36(1):94-98.]

[9]陈京荣,徐瑞华.有偏好的交通网络路径选择模型[J].交通运输工程学报,2012,12(2):100-104.[CHEN J R, XU R H.Route choice model with preferences in traffic network[J].Journal of Traffic and Transportation Engi⁃neering,2012,12(2):100-104.]

[10]Liu H X,Recker W,Chen A.Uncovering the contribu⁃tion of travel time reliability to dynamic route choice us⁃ing real-time loop data[J].Transportation Research Part A:Policy and Practice,2004,38(6):435-453.

[11]Goh C H,Tung Y C A,Cheng C H.A revised weighted sum decision model for robot selection[J].Computer& Industrial Engineering,1996,30(2):193-199.

[12]Jahanshahloo G R,Hosseinzade L,Izadikhah M.An algo⁃rithmic method to extend TOPSIS for decision-making problems with interval data[J].Applied Mathematics and Computation,2006,175(2):1375-1384.

[13]Zhang Jijun,Wu Desheng,Olson D L.The method of grey related analysis to multiple attribute decision mak⁃ing problems with interval numbers[J].Mathematical and Computer Modeling,2005,42:991-998.

Grey Relational Analysis for Multi-attributes Decision Making of Route Choice with Subjective Preference

ZHENG Jian-hu，WU Xiong-bin，HUANG Ming-fang，WEN Zi-juan
(Transportation Engineering Institute of Minjiang University,Fuzhou 350108,China)

ract:Route choice model is core problem of dynamic traffic guidance.With respect to the traveler’s different preference and incompletely specified route-attribute,a new model with Subjective Preference is proposed which take interval values as the characteristics of route multi-attributes.With the degree of traffic congestion,travel time,route distance and the reliability of travel time,an indicator system of route choice is presented.Then,giving the interval values of objective and subjective,the relational coefficients between subjective preference and objective values of every alternative route are obtained.In order to reduce the error between the subjective and the objective values,an optimal model is provided to get the attribute weights. Furthermore,all alternative routes are ranked according to the relational degree.In the end,a numerical example is given with the real network of 3 lanes and 7 alleys in Fuzhou,and the results show that the proposed method is simple and effective.

rds:intelligent transportation;route choice;grey relational analysis;multi-attributes;traveler’s preference

1009-6744（2014）02-0168-05

U491

A

2013-11-13

2014-02-16录用日期：2014-02-24

福建省自然科学基金项目（2012J01281）；闽江学院科技育苗项目（YKY13016）.

郑建湖（1975-），男，福建福州人，副教授，博士. *

zjianhu1028@163.com