基于聚类中值比较的WSNs故障检测算法*

张 成

(北京交通大学 电子信息工程学院,北京 100044)

基于聚类中值比较的WSNs故障检测算法*

张 成

(北京交通大学 电子信息工程学院,北京 100044)

无线传感器网络(WSNs)中的传感器件容易失效而导致测量数据不准确，因而，高效、实用的故障检测算法对于保证WSNs的感知质量非常重要。提出一种基于聚类中值比较(CBMC)的故障检测算法。不同于传统的中值比较的思想，该算法引入聚类方法对待检测节点的邻居节点测量数据进行分组，根据分组信息计算该节点状态。仿真实验表明:CBMC算法具有较高的故障检测率(DR)和较低的故障误检率(FPR)。

无线传感器网络； 聚类中值比较； 故障诊断； 故障检测； 故障容错

0 引 言

最近几年，随着无线传感器网络(WSNs)研究的深入，故障检测和容错逐渐成为研究热点[1～13]。Ruiz L B等人提出一个基于事件驱动的故障管理框架MANNA[1]。该框架是第一个比较完整的WSNs管理解决方案，详细分析WSNs故障管理的需求、目标、体系结构等,但是该框架采用集中式管理方式，能量消耗较大,对于能量有限的WSNs，该方案存在较大局限。Chessas S和Santi P在研究了Ad Hoc网络故障诊断[2]的基础上，提出了基于WSNDiag协议的故障定位算法[3]。这种方法可以很好地解决WSNs崩溃故障的诊断，但对于非崩溃型故障是不适用的，特别是对于传感器件的故障，适用性较差。Krishnamachari B等人基于WSNs测量的空间连续性假设和节点故障的独立性假设[4]，提出了随机决策算法、门限决策算法和最优门限决策算法(optimal threshold detection scheme，OTDS)等3种检测算法[5]。其中，故障检测效果最好的OTDS在本质上是一种多数表决策略。 Luo X W等人对上述方法做了进一步分析和改进，考虑如何解决噪音环境下测量错误和传感器故障并发状况下的故障检测问题，并提出确定最佳邻居数目的算法[6]。Ding M等人提出了本地诊断算法[7]，采用中值策略，通过邻居节点的读数来校验节点的状态。这种方法的特点是节省能耗、分布式本地检测，但算法的检测性能还需要进一步提高。Tian Q J等人和高建良等人各自独立地提出了基于加权中值的故障检测算法[8，9](weighted fault median detection scheme，WFMDS)。该算法在中值故障检测算法的基础上，降低疑似故障节点的分析权重，改进了检测效果。

本文提出一种基于聚类中值比较(clusting-based medium comparison,CBMC)的故障检测算法。该算法的创新性在于提出基于聚类的节点测量数据的组织方法，并根据聚类结果产生的组与组数确定节点的状态。基于聚类的非监督分类方法降低了故障检测策略对异常数值和数据偏度的敏感度，这在很大程度上提高了故障检测性能。

1 WSNs模型

WSNs中可能发生的故障有多种，按故障发生范围，可分为器件级、节点级、网络级故障[10,11]。后两类故障常导致节点间无法正常通信，可通过拓扑算法和路由算法发现，因此,本文不考虑这两类故障。在WSNs组成部件中，计算、存储、通信、电池等器件的故障检测和容错技术相对比较成熟，故障概率相对较小，而对于直接暴露于外界环境负责感知测量的低成本的传感器件则更容易出错。传感器件处于故障状态时，通常表现为测量数据错误或偏移,这使WSNs监测结果出现重大偏差，甚至无法使用。本文以传感器件故障作为研究对象。

采用图G=(V，E)作为WSNs模型，其中,V为所有节点集合，E由节点间距离在节点通信范围内的可相互通信的节点对组成。设WSNs所有节点具有相同的通信半径，节点状态可分为正常态和故障态。当节点故障时，相比于正常时测量值会偏高或偏低。

为简化研究，忽略无关细节，采用与现有研究类似的假设前提：WSNs密集部署，处于事件区域边界的节点可忽略；监测对象的测量值具有空间连续性，节点与邻居节点在正常态时具有近似测量值[4]；各节点传感故障的发生具有独立性；节点处于故障态时感知的测量值比其处于正常态时偏高或偏低，其差异明显可区分。

2 WSNs故障检测算法

2.1 问题定义

设WSNs中任一节点vi，其感知区域的真实值为γi，节点的测量值为M(vi)，节点故障概率为pi，求节点状态判决函数D(vi)。理想的D(vi)函数，在vi处于正常态时返回True，在vi处于故障态时返回False。设与vi在通信距离内的可相互通信的所有节点为邻居节点，用N(vi)表示，N(vi)={vj|(vi,vj)∈E}。邻居节点数量|N(vi)| 用n表示。N(vi)构成vi所在的“社区”。设邻居节点vj∈N(vi)，1≤j≤n的真实值为γij，节点测量值M(vj)=xij。对于所有vj∈N(vi)，M(vj)组成节点vi的社区测量值，用C(vi)表示。C(vi)={M(vj)|∀vj∈N)vi)}={xi1,xi2,…,xin}，其中设xi1,xi2,…,xin为n个邻居节点读数按照从低到高升序排列。

为节省能量，WSNs采用本地判决策略，基本原理是：在密集部署的WSNs中，目标节点所感知区域的真实值与其各个邻居节点的测量值相近,因此,可由节点所在社区的状态近似确定节点状态。通过一定策略和算法，分析目标节点vi的所有邻居N(vi)的测量值C(vi)，从而形成目标节点所在区域测量值的社区参考值R(vi)。注意，社区测量值C(vi)是一组值，社区参考值R(vi)是一个值。根据C(vi)计算R(vi)时采用的策略通常包括均值策略、中值策略、加权中值策略、多数表决策略等。

2.2 CBMC算法

CBMC算法基本思想如下：目标节点vi通过将自身测量值M(vi)与其社区参考值R(vi)进行比较，以获取对自身测量值是否准确的判断，进而确定节点自身状态是否正常。如果两者差异在某一门限α之内，则认为目标节点vi状态正常。与传统的均值检测、中值检测、多数表决等策略不同，本文提出一种新的CBMC的检测策略。通过聚类算法对社区测量值M(vi)分析后产生m组数据(异常值或高或低于正常值，因而,1≤m≤3)，需要从中寻找可以代表正常状态的组，取其均值用以计算R(vi)。

CBMC算法的输入包括：WSNs的模型G=(V，E)、待检测节点vi、节点状态差异门限α;算法输出为D(vi)=TrueorFalse。

CBMC算法具体步骤如下：

1)在WSNs中，任选一待检测节点vi，获得测量值为M(vi)，邻居节点测量值的集合为C(vi)。

2)采用聚类算法Cluster(M(vi))，进行分组，形成由低到高的S1,S2,…,Sm等m个组，1≤m≤3。

对m的数值进行判断：

m=1：R(vi)=mean(Sm)；∥mean取中值;

m=2：将M(vi)按顺序插入C(vi)，重新调用聚类算法Cluster(M(vi))分组，形成由低到高的S1,S2,…,Sm′等m′个组，1≤m′≤3。

①若m′为1，则R(i)=mean(Sm′)；

②若m′为2，并且|Sm′/2|>|S(m′/2+1)|, 则R(i)=mean(Sm′/2);否则,R(i)=mean(S(m′/2+1));

③若m′为3，则R(i)=mean(S(m′+1)/2),m=3:R(i)=mean(S(m+1)/2).

3)节点状态判断：通过节点vi将自身测量值M(vi)与R(vi)比较来求解D(vi)：如果|M(vi)-R(vi)|/M(vi)≤α，则D(vi)=Ture，vi为正常节点；否则,D(vi)=False，vi为故障节点。

Cluster(M(vi))算法描述如下：

1)将M(vi)中的数据从低到高排序，不妨设顺序为：xi1,xi2,…,xin；

2)设θj=(xi,(j+1)-xij)/xij，根据斜率θj的高低判断数据分组，得到θ1,θ2,…,θn-1。

3)从θ1到θn-1遍历，如果θj≥α，则θj为组边界节点(新组的开始)。按照组边界节点的划分形成分组S1,S2,…,Sm。

4)如果m>3，则α=1.1α，跳转至步骤(3)；

5)输出分组信息：S1,S2,…,Sm。

在聚类算法Cluster(M(vi))的第4步中，由于已经分析得出1≤m≤3,如果出现m>3，说明算法中的α门限值设置过低，有必要进行少量上调，可以设置为1.1α。Cluster(M(vi))输出的不同的组数m代表的意义不同：当m=1，则这一组数据可能都是正常的，或偏高故障的，或偏低故障的；当m=2，则这2组的数目可能是正常+偏高，或正常+偏低,或偏高+偏低；当m=3，则这些数据中包括正常、偏高、偏低各种情况，而居中的那组数据很可能是正常数据。

2.3 参数分析

CBMC算法中涉及节点状态差异门限 。该参数是用来区分正常态下的测量值与故障态下的测量值(包括故障态偏高测量值和故障态偏低测量值)。该值过大与过小都会对算法造成影响，过大，则无法区分正常态下的测量值与故障态下的测量值;过小，则可能造成误判，即把同处正常态(或故障态)的测量值，错误地分开。

设正常态、故障态偏高、故障态偏低等情况的测量值分别为随机变量ηn,ηh,ηl，则

Δαhn=(min(ηh)-max(ηn))/max(ηn)，

Δαnl=(min(ηn)-max(ηl))/min(ηn)，

Δαh=(max(ηh)-min(ηh))/min(ηh)，

Δαn=(max(ηn)-min(ηn))/min(ηn)，

Δαl=(max(ηl)-min(ηl))/min(ηl),

于是有

max(Δαn,Δαh,Δαl)≤α≤min(Δαhn,Δαnl).

(1)

理想的α应满足式(1)。在应用中，考虑到随机变量中ηn,ηh,ηl可能存在某些小概率极端值，可能没有满足式(1)的解。因此,在进行max，min运算时，必要时需要对随机变量ηn,ηh,ηl的取样进行处理，以避免极端值的影响，即剔除发生概率非常小的极端样本。在本文的仿真实验中，α设为0.4。

2.4 能耗分析

由于WSNs的主要能耗来自于通信开销，因而主要分析算法的通信开销。对于社区测量值C(vi)的监听，采用共享的广播信道，CBMC与OTDS,WMFDS算法等一样，都需要接收社区测量值的通信开销，开销没有区别。

然而在实际部署时，没有必要实时地每次都去获取临近节点的节点状态。邻居节点之间节点状态消息的传送频率，与节点故障发生的速率有关，即节点经过多久才会发生故障。考虑到可以每隔一段时间节点依次交替地传送最新的节点状态，所以,CBMC算法的额外通信开销是很小的。

3 仿真结果和分析

3.1 仿真实验

为了验证和比较CBMC算法的性能，采用文献[12]的实验环境和参数并通过Matlab加以实现。该实验环境具体包括如下2个模块：1)WSN—DEPLOY—NODE模块:输入参数为节点个数、部署类型(随机部署或网格部署)、检测区域、节点故障率。该模块根据节点故障概率随机生成故障节点；包括正常节点和故障节点的所有节点，周期性进行环境监测，所得读数设置到节点读数属性。设节点vi所在区域的真实值为γi=100，当节点处于正常状态时，其测量值为M(vi)=γi+εn，当节点处于测量值偏高的故障状态时，设其测量值为M(vi)=γ+Δ+εh；当节点处于测量值偏低的故障状态时，设其测量值为M(vi)=γi-Δ+εl。其中，Δ=50，εn,εh,εl分别服从正态分布N(μ,δ)的测量噪声μ=0，δ=20。实验中WSNs节点数为32×32=1 024，采用网格方式部署。2)WSN—FIND—FAUT模块:支持的算法包括MFDS基于中值的故障检测算法、WMFDS基于加权中值的故障检测算法、MEAN基于均值的故障检测算法、OTDS基于多数表决的故障检测算法、基于CBMC的故障检测算法。

设WSNsG=(V,E)中，正常态节点的集合为VN，故障节点的集合VF，引入如下度量指标：

1)节点故障检测率(detection rate，DR)

2)节点故障误检率(false positive rate，FPR)

3.2 结果分析

下面给出WSNs通信半径r=1.5(邻居节点为4个节点的场景一)和r=2(邻居节点为8个节点的场景二)两类场景下的仿真结果。

场景一下的DR如图1所示。CBMC算法的DR要高于OTDS算法，低于MEAN，MFDS,WMFDS算法。FPR如图2所示,CBMC算法的FPR要明显低于MFDS，WMFDS，MEAN，OTDS算法。可见在场景一下，CBMC算法具有较高的DR和相当低的FPR。当DR达到一定程度后，FPR就格外重要，因而，CBMC算法具有明显优越性。这在一定程度上说明了基于聚类数据分组的故障检测策略的有效性。

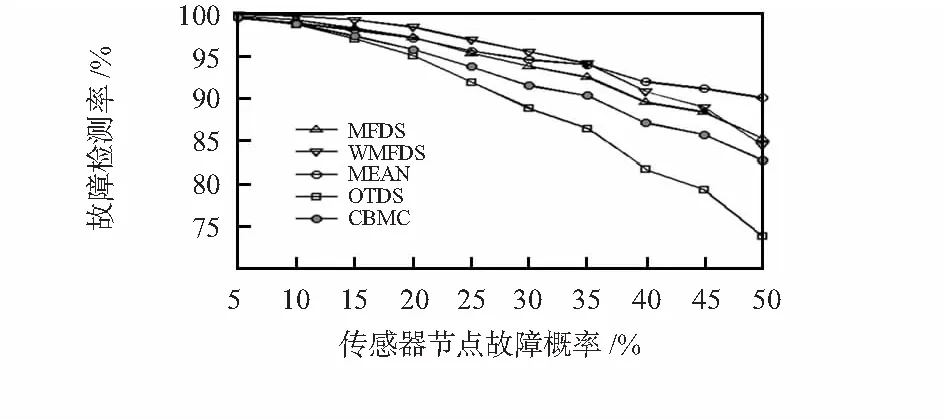
图1 4个邻居节点的DRsFig 1 DRs in 4-neighbour nodes

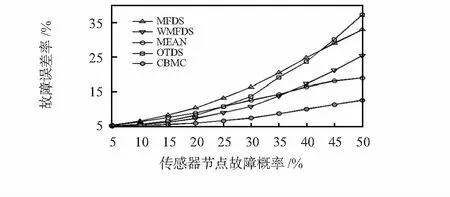
图2 4个邻居节点的FPRsFig 2 FPRs in 4-neighbour nodes

场景二下的DR如图3所示。CBMC算法的DR要明显优于OTDS，MEAN，MFDS算法，在节点故障率为15 %～35 %时，CBMC算法的性能与WMFDS算法略低或基本相当。在节点DR超过35 %时，CBMC算法的DR则要明显优于WMFDS算法。FPR如图4所示。CBMC算法的FPR要明显低于MFDS,WMFDS,MEAN,OTDS算法。CBMC算法在邻居节点增多的情况下，表现出更好的故障检测性能。较多的邻居节点虽然可以增大故障的检测效果，却是以增加通信开销和能耗为代价的。具体应用时，需综合考虑检测性能与能耗，选择合适的邻居数目。

图3 8个邻居节点的DRsFig 3 DRs in 8-neighbour nodes

图4 8个邻居节点的FPRsFig 4 FPRs in 8-neighbour nodes

4 结 论

本文提出一种新的WSNs故障检测的CBMC算法。该算法采用聚类的非监督式分组机制，可以有效划分和聚合测量数据，进而评估节点所处状态。该机制可以显著提高算法性能，即使在节点故障概率较大的情况下，算法也具有非常理想的DR和FPR。WSNs实际部署环境中，故障的发生具有多样性和复杂性。

[1] Ruiz L B,Nogueira J M,Loureiro A A F.MANNA:A management architecture for wireless sensor networks[J].IEEE Communications Magazine,2003,41(2):116-125.

[2] Chessas S,Santi P.Comparison-based system-level fault diagnosis in Ad Hoc networks[C]∥The 20th Symposium on Reliable Distributed Systems(SRDS),New Orleans,USA,2001:257-266.

[3] Chessas S,Santi P.Crash faults identification in wireless sensor networks[J].Computer Communications,2002,25(14):1273-1282.

[4] Vuran M C,Akan O B,Akyildiz I F.Spatio-temporal correlation:Theory and application for wireless sensor networks[J].The International Journal of Computer and Telecommunications Networking,2004,45(3):245-259.

[5] Krishnamachari B,Iyengar S.Distributed Bayesian algorithms for fault-tolerant event region detection in wireless sensor network-s[J].IEEE Transactions on Computers,2004,53(3):241-250.

[6] Luo X W,Dong M,Huang Y L.On distributed fault-tolerant detection in wireless sensor networks[J].IEEE Transactions on Computers,2006,55(1):58-70.

[7] Ding M,Chen D,Xing K,et al.Localized fault-tolerant event boundary detection in sensor networks[C]∥IEEE INFOCOM 2005,Miami,USA,2005:902-913.

[8] Tian Q J,Edward J Coyle.Optimal distributed detection in clustered wireless sensor network:The weighted median [C]∥IEEE INFOCOM 2007,Anchorage,Alaska,USA,2007:1-12.

[9] 高建良,徐勇军,李晓维.基于加权中值的分布式传感器网络故障检测[J].软件学报,2007,18(5):1208-1217.

[10] Akbari A,Beikmahdavi N,Khosrozadeh A,et al.A survey cluster-based and cellular approach to fault detection and recovery in wireless sensor networks[J].World Applied Sciences Journal,2010,8(1):76-85.

[11] 刘 凯,彭 力.分簇式无线传感器网络节点故障诊断算法研究[J].传感器与微系统,2011,30(4):37-41.

Fault detection algorithm for WSNs clustering-based medium comparison*

ZHANG Cheng

(School of Electronic and Information Engineering,Beijing Jiaotong University,Beijing 100044,China)

The sensors in WSNs are prone to failure and results in inaccurate measurements,efficient and practical fault detection algorithms is very important to guarantee sensing quality of WSNs.A fault detection algorithm with clustering-based medium comparison(CBMC)is proposed.Different from traditional medium comparison idea,CBMC introduces clustering approach to determine the status by grouping and computing the measurements of neighbor nodes.Simulation results show that the algorithm achieves a high fault detection rate(DR) and a low false positive rate(FPR).

wireless sensor networks(WSNs); clustering medium comparison; fault diagnosis; fault detection; fault tolerant

2013—09—30

国家自然科学基金资助项目(60833002); 北京市自然科学基金资助项目(4091003)

TN 393

A

1000—9787(2014)04—0135—04

张 成(1976-),男,辽宁盘锦人,博士,研究领域为无线传感器网络、通信网络、故障诊断。