参数不确定永磁同步电机混沌系统的单输入状态反馈控制*

唐传胜，戴跃洪，杨红兵

( 电子科技大学 机械电子工程学院， 成都 611731)

参数不确定永磁同步电机混沌系统的单输入状态反馈控制*

唐传胜，戴跃洪，杨红兵

( 电子科技大学 机械电子工程学院， 成都 611731)

针对含有参数不确定的永磁同步电机混沌系统，基于串接系统理论，提出了一种新型的鲁棒状态反馈控制方法。该方法首先将永磁同步电机混沌系统看作由两个子系统组成，即电气子系统和机械子系统。其次，通过对电气子系统设计状态反馈控制器来实现闭环系统的全局渐进稳定。该控制器仅通过控制交轴电压即可实现整个系统的稳定控制，结构简单，具有一定的可实现性。基于Lyapunov稳定理论证明了系统的全局渐进稳定性。仿真结果证实了该方法的有效性。

永磁同步电机；混沌控制；级联系统理论；反馈控制

0 引言

自20世纪90年代混沌现象被发现存在于电机驱动中以来，关于电机驱动中的混沌现象的分析与控制得到广泛关注。混沌现象广泛存在于感应电机、永磁同步电机、直流电机、开关磁阻电机等伺服系统中，国内外学者对其已进行了一定的研究[1-3]。

永磁同步电机当参数处于特定区域时将出现混沌运动[4-5]，这将严重影响电机传动系统的稳定性能，因此有必要对其进行抑制或消除。针对此问题，国内外学者提出了各种控制方法。李忠等[6]人提出纳入轨道和强迁徙控制方法，该方法要求控制目标不允许在收敛系统的任一轨道或状态，并且需要系统轨道处于吸引域中才能施加控制，因而有一定的实现难度；李洁等[7]利用状态延时反馈来实现系统的混沌控制，然而该方法难于确定控制的周期目标轨道与延时时间的关系；又有学者提出诸如状态反馈控制[8-9]、动态面控制[10]、无源控制[11]等，均依赖于系统的数学模型，当系统参数发生变化时，无法保证系统的动态性能，甚至可能导致失控；文献[12]提出了滑模控制，该方法要求系统参数不确定性满足一定的匹配条件，且控制器存在固有的抖振现象；文献[13]提出的自适应控制则需要引入参数自适应机制，必然增加系统的开支，影响系统的响应性能；李和吴等人[14-15]分别将模糊控制应用于PMSM混沌系统，提出了一种模糊控制方法，模糊控制则是建立在系统模型T-S模糊化的基础之上，文献[14]提出的模糊反馈控制系统稳定的时间较长，响应性能有待提高，文献[15]将模糊控制与鲁棒最优控制相结合，提出了模糊最优保代价控制，随其具有较强的鲁棒性，但设计过程过于复杂。

如何设计出一种结构简单且具有抗参数扰动能力的控制器，是本文研究的出发点。文献[16]将串接系统理论应用于混沌系统的同步控制，成功实现了驱动系统与相应系统的全局渐进同步。文献[17]将其推广到解决混沌系统的抑制问题，针对统一混沌系统，提出了一种统一的混沌控制与同步方法。然而，文献[16]和[17]没有考虑到系统中不确定性的影响。实际上，不确定性广泛存在于各种实际系统之中，研究具有不确定性的混沌系统控制与同步问题，更符合实际情况。本文针对含有参数不确定性的PMSM混沌系统，基于串接系统理论，提出一种鲁棒反馈混沌控制策略。通过仿真结果验证了所提出的控制策略的快速响应能力和鲁棒性。

1 理论基础及PMSM混沌模型

1.1 理论基础

串接系统稳定性理论已经在非线性微分几何控制理论中得到比较完善的发展，下面给出串接系统的定义及其稳定性理论的一个重要定理[18]。

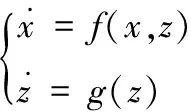
(1)

式中，x∈Rn，z∈Rm为系统的状态；f(x,z)∈Rn×m和g(z)∈Rn×m均是局部Lipschitz的，且满足f(0,0)=0，g(0)=0，这类系统被称为串接系统。

由引理可知，对于混沌系统，由于其状态均有界，因此只要满足引理中的条件①即可保证系统是全局渐进稳定的。

1.2PMSM混沌模型

经过变换后的永磁同步电动机无量纲数学模型[5]为：

(2)

式中，vd、vq和id、iq分别为变换后d轴、q轴的电压和电流；w、TL为变换后的速度和负载，γ、σ为电机参数。

本文仅研究vd=vq=TL=0时电机的混沌现象，该情况相当于电机在运行一段时间之后突然断电，系统在某一参数下呈现的动态特性。由文献[5]的理论分析可知：当γ=20，σ=5.46，初始状态(id,iq,w)=(0.01,0.01,0.01)时，将出现如图1所示的混沌现象(图中的id、iq、w均为标幺值)。

图1 PMSM中的混沌吸引子

考虑系统参数不确定性时，系统(2)可表示为：

(3)

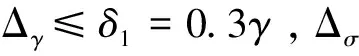
(4)

由机械子系统可知，系统参数σ+Δσ恒为正。当系统的状态iq趋近于零，则机械子系统将全局渐进指数稳定。根据串接系统引理，只要能够设计控制器u，使系统的电气子系统全局渐进稳定，那么整个系统将全局渐进稳定。

因此，我们的控制目标是：设计状态反馈控制u，是受控的参数不确定系统(4)快速镇定道期望的平衡点S0(0,0,0)。

2 控制器设计

针对受控不确定系统(4)，控制器的设计如下所述。

定理：对于不确定性系统(4)，如果采用如下形式的控制器：

(5)

其中，k和L均为为反馈系数且均为正实数，且满足L≥(1+δ1)γ；则系统(4)在平衡点(id,iq,w)=(0,0,0)是全局渐进稳定的。

证明：对于系统(4)中的电气子系统，把控制器u代入可得：

(6)

故平衡点(id,iq)=(0,0)是电气子系统全局渐进稳定的。

若状态(id,iq)达到其平衡点(id,iq)=(0,0)所需的时间为T1，则当t>T1时，(id,iq)≡(0,0)。将(id,iq)=(0,0)代入(4)中的机械子系统，可得：

(7)

显然平衡点w=0亦是响应子系统全局渐进稳定的，故引理1中的条件①得到满足；又系统(3)是混沌系统，因此其各个状态是有界的，条件②亦满足，从而由引理可知，系统(4)在平衡点(id,iq,w)=(0,0,0)是全局渐进稳定的，定理得证。

3 仿真与分析

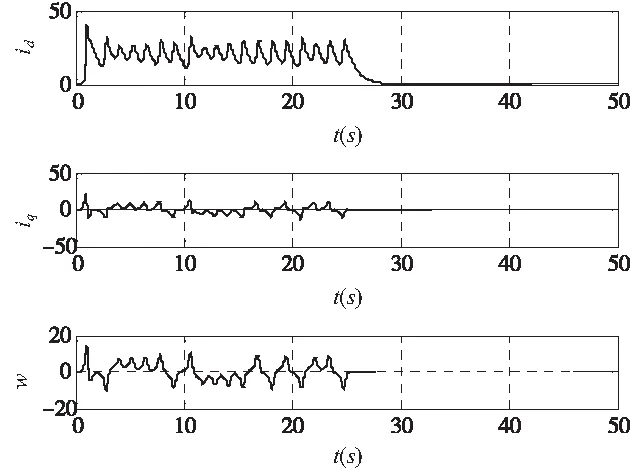
本部分主要是通过仿真实验来验证本文方案的有效性。仿真中均采用四阶Runge-Kutta法，采样时间Ts=0.01s,初始条件(id0,iq0,w0)=(0.01,0.01,0.01)，γ=20，σ=5.46。下面对含有参数不确定性和不含参数不确定性两种情况分别进行仿真研究。

(a)状态轨迹

仿真结果分析：由图2a可知，系统不含参数不确定性时，电流id、iq和速度w都能趋近于平衡点(0,0,0)，然而id的趋近速度明显低于iq和w，这是由于三者均是以指数形式趋近于平衡点，但w和iq对应的系数分别为σ=5.46和k+1=2均大于id对应的系数1，因此状态iq和w明显比id的响应速度快。图2b为控制器输出，从图中可以看出控制器输出光滑，且能够快速稳定到某一常值。

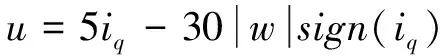
(a)状态轨迹

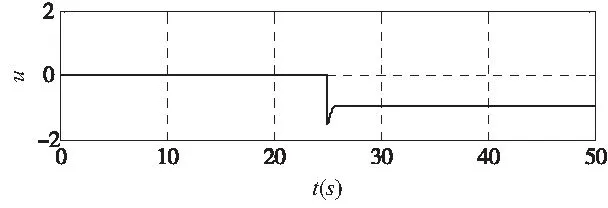
(b)控制输入

(a)状态轨迹

(b)控制输入

仿真结果分析：由图3、图4可知，系统无论存在参数正摄动还是负摄动，其各个状态电流id、iq和速度w均能趋近于系统的平衡点(0,0,0)，然而id的趋近速度仍明显低于iq和w，原因同上。与不含参数不确定性时的最大区别在于：由于系统参数不确定的存在，致使系统的状态变化范围增大，控制器的输出也随之变化，系统达到平衡时控制器输出保持恒定，即相当于给系统施加恒定的电压。

总之，无论系统是否存在参数不确定性，本文的方案都能有效的使系统的状态趋近于其平衡点，控制过程平稳光滑，具有很好的控制效果。

4 结论

本文研究了含有参数不确定性的PMSM混沌系统的控制问题。基于串接系统理论，将PMSM混沌系统分解为电气子系统和机械子系统，通过电气子系统设计简单的鲁棒反馈控制器，来实现整个系统的渐进稳定。基于Lyapunov稳定理论，证明了系统的全局渐进稳定性；并通过仿真实验，验证了采用本方案的控制系统不仅在无参数不确定性时具有较好快速响应能力，而且存在不确定性时也能很好的满足系统性能的要求，具有一定的研究价值。

[1] 邹国堂，王政，程明. 混沌电机驱动及其应用[M]. 北京:科学出版社, 2009.

[2]HematiN.StrangeattractorsinbrushlessDCmotors[J].IEEETransactionsonCircuitsandSystems-Ⅰ:FundamentalTheoryandApplications. 1994, 41(1): 40-45.

[3] 张波, 李忠, 毛宗源, 等. 一类永磁同步电动机混沌模型与霍夫分叉[J]. 中国电机工程学报, 2001, 21(9):13-17.

[4] 张波，李忠，毛宗源，等. 电机传动系统的不规则运动和混沌现象初探[J]. 中国电机工程学报, 2001, 21(7): 40-45.

[5]LiZ,ParkJB,JooYH,ZhangB,ChenGR.Bifurcationsandchaosinapermanentmagnetsynchronousmotor[J].IEEETransactionsonCircuitsandSystems-Ⅰ:FundamentalTheoryandApplications, 2002, 49(3): 383-387.

[6] 李忠，张波，毛宗源. 永磁同步电动机系统的纳入轨道和强迫迁徙控制[J].控制理论与应用,2002, 19(1):53-56.

[7] 李洁, 任海鹏. 永磁同步电动机中混沌运动的部分解耦控制[J]. 控制理论与应用, 2005, 22(4):637-640.

[8] 任海鹏，刘丁，李洁. 永磁同步电动机中混沌运动的延时反馈控制[J]. 中国电机工程学报, 2003, 23(6): 175-178.

[9] 韦笃取, 罗晓曙. 非均匀气隙永磁同步电机混沌的状态反馈控制[J]. 广西师范大学学报: 自然科学版, 2006, 24(1): 13-17.

[10]WeiDQ,LuoXS,WangBH,FangJQ.Robustadaptivedynamicsurfacecontrolofchaosinpermanentmagnetsynchronousmotor[J].PhysicLetterA, 2007, 363: 71-77.

[11] 吴忠强，谭拂晓. 永磁同步电动机混沌系统的无源化控制[J]. 中国电机工程学报, 2006, 26(18): 159-163.

[12] 韩建群, 郑萍. 永磁同步电动机中混沌运动的滑膜控制[J]. 系统工程与电子技术, 2009, 31(3): 723-725.

[13] 韦笃取, 张波, 邱东元, 等. 基于LaSalle不变集定理自适应控制永磁同步电动机的混沌运动[J]. 物理学报, 2009,58(9): 6026-6029.

[14] 李东, 张小洪, 杨丹, 等. 参数不确定永磁同步电机混沌的模糊控制[J]. 物理学报, 2009, 58(3): 1430-1440.

[15] 吴忠强. 非线性系统的最优模糊保代价控制及其在永磁同步电动机混沌系统中的应用[J]. 中国电机工程学报, 2003, 23(9): 152-157.

[16]WangH,HanZZ,MoZ.Synchronizationofhyperchaoticsystemsvialinearcontrol[J].CommumNonlinearSciNumerSimulat, 2010(1): 1910-1920.

[17]WangH,HanZZ,ZhangW,XieQY.Chaoscontrolandsynchronizationofunifiedchaoticsystemsvialinearcontrol[J].Journalofsoundandvibration, 2009, 320: 365-372.

[18]SundarapandianV.Globalasymptoticstabilityofnonlinearcascadesystems[J].AppliedMathematicsLetters, 2002, 15: 275-277.

(编辑 赵蓉)

Single Input State Feedback Control of Chaos in Permanent Magnet Synchronous Motor with Uncertain Parameters

TANG Chuan-sheng，DAI Yue-hong，YANG Hong-bing

(School of Mechatronics Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

This paper concerned with the problem of controlling chaos in permanent magnet synchronous motor (PMSM) with parametric uncertainties. Based on cascade-connected system theory (CCST), a novel robust state feedback control scheme is proposed. First，PMSM chaotic systems can be regarded as two subsystems：electrical subsystem and mechanical subsystem. Then, a state feedback controller is designed for electrical subsystem to make the closed system asymptotically stable. Only by controlling the cross-axis voltage, it can guarantee the whole system global asymptotically stability. Moreover, the presented controller has a simple structure to realize. The stability of the closed-loop system is demonstrated via Lyapunov stability theory. Simulation results verify the effectiveness of the proposed method.

PMSM; chaos control; cascade-connected system theory; feedback control

1001-2265(2014)04-0049-04

10.13462/j.cnki.mmtamt.2014.04.013

2013-08-02

国家重大科技攻关项目(2009ZX04001)

唐传胜 (1982—)，男，河南南阳人，电子科技大学博士研究生，研究方向为伺服系统控制、非线性系统分析与控制，(E-mail)tcs111@163.com。

TH164;TG65

A