区间软RSL-代数
许宏伟, 刘卫锋, 张理涛
(郑州航空工业管理学院 数理系 河南 郑州 450015)
区间软RSL-代数
许宏伟, 刘卫锋, 张理涛
(郑州航空工业管理学院 数理系 河南 郑州 450015)
将区间软集应用于RSL-代数,定义了区间软RSL-代数、区间软RSL-子代数、区间软RSL-代数的软同态等概念,讨论了它们的基本性质,推广了相关文献中软RSL-代数的结果.
软集; 区间软集; RSL-代数; 软RSL-代数; 区间软RSL-代数
0 引言
文[1]中提出了软集的概念,为研究不确定性问题提供了一种新的方法.由于软集与模糊集、粗糙集等理论具有较强的互补性,因此软集理论受到了许多学者的关注和研究.在文[1]基础上,文[2-4]定义了软集的各种运算和软相等概念;文[6-8]将文[5]提出的区间集应用于软集,提出了区间软集的概念;文[9-14]分别提出了软群、软环、软半环、软Quantale、软坡、软格等概念,并研究了它们的性质;文[15-17]分别研究了软BCK/BCI代数、软BL代数、软RSL-代数.但是,目前没有发现将区间软集应用于代数结构之中的报道,为此本文尝试将区间软集应用于RSL-代数,提出了区间软RSL-代数、区间软RSL-子代数和区间软RSL-代数的软同态等概念,并对它们的一些基本性质进行了探讨.本文推广了文[17]中软RSL-代数的相关结果.
1 相关概念
定义1[18-19]代数结构(L,∨,∧,*,+,⊗,→,0,1)称为RSL-代数,如果(L,∨,∧,*,+,0,1)为正则双Stone-代数,(L,∨,∧,⊗,→,0,1)为IMTL-代数.
为方便起见,以后用L,L1,L2表示RSL-代数.
定义2[17]设(F,A)是RSL-代数L上的软集,若∀x∈A,F(x)均为L的子代数,则称(F,A)是L上的一个软RSL-代数.
定义3[1]设X是论域,P(X)是其幂集,E是指标集,A⊆E,F:A→P(X)是一个映射,则称(F,A)是X上的一个软集.

定义5[6-8]设X是论域,E是指标集,A⊆E,F:A→I(P(X))是一个映射,称(F,A)是X上的一个区间软集,其中I(P(X))表示X上的所有区间集之集合.
I(P(X))上的偏序集定义为[Al,Au],[Bl,Bu]∈I(P(X)),[Al,Au]≤[Bl,Bu]⟺Al⊆Bl,Au⊆Bu.
定义6[8]设(F1,A1),(F2,A2)是X上的区间软集,则定义如下运算:

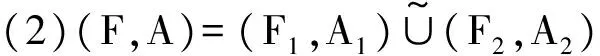
(3)(F,A)=(F1,A1)∩ε(F2,A2),其中A=A1∩A2,∀x∈A,F(x)=F1(x)∩F2(x).
(4)(F,A)=(F1,A1)∧(F2,A2),其中A=A1×A2,∀(x,y)∈A1×A2,F(x,y)=F1(x)∩F2(y).
2 区间软RSL-代数
定义7 设(F,A)是RSL-代数L上的区间软集,若∀x∈A,F(x)=[Al,Au],且Al,Au为L的RSL-子代数,则称(F,A)是L上的一个区间软RSL-代数.
若∀x∈A,F(x)=[Al,Au],其中Al=Au,则区间软RSL-代数退化为软RSL-代数,故而区间软RSL-代数是软RSL-代数的推广.
下面在文[17]中RSL-代数实例基础上,说明区间软RSL-代数是存在的.
例1 设L={0,a,b,c,d,e,f,1},定义L的运算*,+,⊗,→和序关系如图1和表1~3,则(L,∨,∧,*,+,⊗,→,0,1)是一个RSL-代数.

图1 RSL代数L

0abcdef1∗1fedcba0+1fedcba0

表2 L上的→运算Tab.2 →operation on L

表3 L上的⊗运算Tab.3 ⊗ operation on L
令A={x,y,z},设(F,A)是L上的区间软集,其中
F(x)=[{0,1},{0,a,f,1}],F(y)=[{0,b,e,1},L],F(z)=[{0,c,d,1},L].
可以验证(F,A)是L上的区间软RSL-代数.



推论1 设(F1,A1),(F2,A2)是L上的区间软RSL-代数,若A1∩A2≠∅,则(F1,A1)∩ε(F2,A2)是L上的区间软RSL-代数.


定理4 设(F1,A1),(F2,A2)是L上的区间软RSL-代数,则(F1,A1)∧(F2,A2)是L上的区间软RSL-代数.

现将上述结论推广到任意指标集.
定理5 设(Fi,Ai)(i∈I,I为指标集)是L上的区间软RSL-代数,则
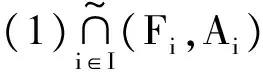

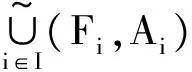

3 区间软RSL-子代数
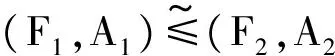

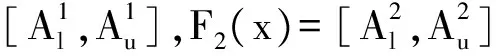



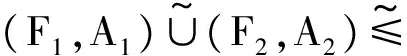




定义9 设(F,A)是L上的区间软RSL-代数.若∀x∈A,F(x)=[{0},{0}]={0},其中0为RSL-代数L的最小元,则称(F,A)为平凡的.若∀x∈A,F(x)=[L,L]=L,则称(F,A)为完整的.
定义10 设f:L1→L2为集合L1到L2的同态映射,(F,A)是L1上的区间软集,定义L2上的区间软集如
f(F):A→I(P(L2)),
f(F)(x)=f(F(x))=f[Al,Au]=[f(Al),f(Au)],∀x∈A,其中Al,Au∈I(P(L1)).
定理9 设f:L1→L2为L1到L2的同态映射,则
(1)若(F,A)是L1上的区间软RSL-代数,且∀x∈A,有F(x)=kerf,则(f(F),A)是L2上的平凡区间软RSL-代数.
(2)若f为满射,且(F,A)是L1上的完整区间软RSL-代数,则(f(F),A)是L2上的完整区间软RSL-代数.
证明 (1)已知∀x∈A,F(x)=kerf,于是,∀x∈A,有f(F)(x)=f(F(x))={02}=[{02},{02}],其中02为L2中的最小元,因此(f(F),A)是L2上的平凡区间软RSL-代数.
(2)由题设可知,f(L1)=L2,且∀x∈A,有F(x)=[L1,L1]=L1.于是,∀x∈A,f(F)(x)=f(F(x))=f(L1)=L2=[L2,L2],故(f(F),A)是L2上的完整区间软RSL-代数.
定理10 设f:L1→L2为L1到L2的同态映射.若(F,A)是L1上的区间软RSL-代数,则(f(F),A)是L2上的区间软RSL-代数.
证明 由于(F,A)是L1上的区间软RSL-代数,故∀x∈A,F(x)=[Al,Au],其中Al,Au是L1的子代数,又f为同态映射,所以f(F)(x)=f(F(x))=[f(Al),f(Au)],其中f(Al),f(Au)是L2的子代数.故(f(F),A)是L2上的区间软RSL-代数.


4 区间软同态
定义11 设(F1,A1),(F2,A2)分别是L1,L2上的区间软RSL-代数,f:L1→L2,g:A1→A2是两个映射.如果f为同态映射,且∀x∈A1,f(F1(x))=F2(g(x)),则称(f,g)为从(F1,A1)到(F2,A2)的区间软同态.
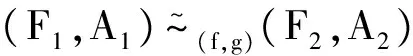
定理12 设(F1,A1),(F2,A2)分别是L1,L2上的区间软集,如果(F1,A1)为L1上的区间软RSL-代数,且(F1,A1)与(F2,A2)区间软同态(构),则(F2,A2)为L2上的区间软RSL-代数.

[1] Molodtsov D. Soft set theory—first results[J].Computers and Mathematics with Applications,1999,37(4):19-31.
[2] Maji P K, Biswas R, Roy A R. Soft set theory[J].Computers and Mathematics with Applications,2003,45(4): 555-562.
[3] Ali M I, Feng F, Liu X, et al. On some new operations in soft set theory[J]. Computers and Mathematics with Applications,2009,57(9):1547-1553.
[4] Qin K, Hong Z. On soft equality[J]. Journal of Computational and Applied Mathematics,2010,234(5):1347-1355.
[5] Yao Y Y. Interval set algebra for qualitative knowledge representation[C]//Proceedings of the 5th International Conference on Computing and Information. Ontario,1993.
[6] 付清.模糊软集及其在决策中的应用[D].宁波:宁波大学,2012.
[7] 张小红,裴道武,代建华.模糊数学与Rough集理论[M].北京:清华大学出版社,2013:34-35.
[8] Qin K Y, Meng D, Pei Z,et al. Combination of interval set and soft set[J]. International Journal of Computational Intelligence Systems, 2013, 6(2): 370-380.
[9] Aktas H, Cagman N. Soft sets and soft groups[J].Information Sciences,2007,177(3):2726-2735.
[10] Acar H, Koyuncu F, Tanay B. Soft sets and soft rings[J].Computers and Mathematics with Applications, 2010,59(11):3458-3463.
[11] Feng F, Jun Y B, Zhao X Z. Soft semirings[J].Computers and Mathematics with Applications, 2008, 56(10): 2621-2628.
[12] 肖旗梅,李庆国.软Quantale[J].计算机工程与应用,2012,48(6):21-23.
[13] 廖祖华,芮明力.软坡[J].计算机工程与应用,2012,48(2):30-32.
[14] 邵迎超,朱振国,秦克云.软集与软格[J].计算机工程与应用,2013,49(3):10-14.
[15] Jun Y B. Soft BCK/BCI algebras[J].Computers and Mathematics with Applications,2008,56(5):1408-1413.
[16] Zhan J, Jun Y B. Soft BL-algebras based on fuzzy sets[J].Computers and Mathematics with Applications, 2010,59(6):2037-2046.
[17] 邵迎超,秦克云.软集与软RSL-代数[J].计算机工程与应用,2011,47(27):15-18.
[18] 张小红.模糊逻辑及其代数分析[M].北京:科学出版社,2008.
[19] Duentsch I, Winter M. Rough relation algebras revisited[J].Fundamenta Informaticae, 2006,74(2):283-300.
Interval Soft RSL-algebras
XU Hong-wei, LIU Wei-feng, ZHANG Li-tao
(DepartmentofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China)
The notion of interval soft sets was applied to RSL-algebras. The concepts of interval soft RSL-algebras, interval soft RSL-subalgebras and soft homomorphism between interval soft RSL-algebras were defined and some basic properties were discussed. The results of soft RSL-algebras in related reference were generalized.
soft sets; interval soft sets; RSL-algebras; soft RSL-algebras; interval soft RSL-algebras
2013-03-19
国家自然科学基金数学天元基金资助项目,编号11226337;河南省教育厅科学技术研究重点项目,编号12B110027.
许宏伟(1957-),男,副教授,硕士,主要从事应用数学研究,E-mail:xhwzzia@163.com.
O 153
A
1671-6841(2014)01-0037-05
10.3969/j.issn/1671-6841.2014.01.009

