基于Vague集记分函数的一种构造方法
王万军
(兰州文理学院 信息工程学院 甘肃 兰州 730000)
基于Vague集记分函数的一种构造方法
王万军
(兰州文理学院 信息工程学院 甘肃 兰州 730000)
在分析已有Vague集记分函数的基础上,构造了一种新的Vague集记分函数,该记分函数能有效地刻画不同风险偏好关系,克服了传统记分函数的缺陷与不足.讨论了新构造记分函数的涵义及构造准则.最后,通过实例分析比较了该记分函数的可行性和有效性.
Vague集; 记分函数; 构造方法
0 引言
自从Zadeh于1965年提出Fuzzy集[1]以来,Fuzzy集已被成功应用到社会诸多领域.Fuzzy集是通过定义在[0,1]上的一个单值隶属函数来刻画模糊问题,但实际上Fuzzy集无法表示支持(肯定)、反对(否定)和犹豫(不确定)的证据.Gau和Buehrer于1993年推广了Fuzzy集,提出了同时能考虑隶属与非隶属2个方面信息的Vague集[2].Vague集定义了一个[0,1]区间上真隶属函数tA(x)和假隶属函数fA(x)来刻画信息的模糊性,Vague集克服了Fuzzy集的不足与缺陷,在信息处理、工业控制、决策分析及模式识别等领域得到广泛应用.但作为Vague集关键问题之一的记分函数研究,目前虽然一些学者进行了相关研究[3-11],但仍然存在许多问题.
本文针对目前Vague集记分函数相关文献及资料,结合不同决策者风险偏好情况,构造了一种带偏好风险决策的Vague集记分函数.通过实例比较分析,发现该方法是一种可行有效的记分函数.
1 已有Vague集记分函数不足及分析
已有文献中具有代表性Vague集记分函数,主要有如下几种:
(1)Chen与Tan的记分函数[3]
Chen与Tan于1994年首次提出了Vague集的记分函数SC(x)=tx-fx.SC(x)只考虑了支持证据tx与反对证据fx,该记分函数容易造成信息丢失,甚至结果的错误.
为了弥补Chen等人方法的不足,文献[4]提出用精度函数H(x)=tx+fx来判断SC(x)相同时决策信息优劣.
(2)李凡等人的记分函数[5]

李凡等人的记分函数只考虑了2种极端(悲观决策与乐观决策),没有考虑中立状态,有不足之处.
(3)刘华文的记分函数[6]
该记分函数将未知度πx进行二次分配,给支持度tx,反对度fx与犹豫度(1-tx-fx)πx3部分进行构造新的记分函数,即SL(x)=tx+(1-tx-fx)tx.SL(x)记分函数的最大不足是:对任意Vague值tx=0,则恒有SL(x)=0,显然这是不合理的.
(4)周珍等人的记分函数[7]
该记分函数为SZ(x)=tx-fx+(α-β)πx,其中参数α,β∈[0,1],α+β∈[0,1].该记分函数的缺点是参数α,β的选择比较难掌握,由于α,β选择不当导致结果不合理.
(5)Ye J的记分函数[9]
Ye J将记分函数定义为SY(x)=tx-fx+μπx,其中参数μ∈[-1,1].该记分函数缺点与SZ(x)记分函数一样,参数μ选择不恰当会导致结果的不合理或不正确.
(6)王伟平的记分函数[10]
该记分函数定义为
SME(x)记分函数根据决策者中立、厌恶与追求心态构造了一种分段的记分函数,虽然该方法能较好地反映决策者偏好心态,但该记分函数在信息决策时容易造成信息偏好极端化,即当支持证据占优势时,采用追求心态决策时未确知信息πx全部激进支持证据;当反对证据占优势时,采用厌恶心态决策时,未确知信息πx全部追随反对证据.从理论上来说是不合理的.
2 Vague集及记分函数
2.1 Vague集
定义1[2]设U是一个论域,∀x∈U,对U上的一个Vague集描述用一个真隶属函数tA(x)和一个假隶属函数fA(x)来表示.即tA(x):U→[0,1],fA(x):U→[0,1],其中tA(x)+fA(x)∈[0,1].
tA(x)描述了支持证据的隶属度下界,fA(x)描述了反对证据的隶属度下界.
定义2 称[tA(x),fA(x)]是x在Vague集A上的Vague值,πA(x)=1-fA(x)-tA(x)是x在Vague集A上的未知度或犹豫度.
πA(x)反映了x相对A的未知信息量,πA(x)越大,未知信息量越多,当πA(x)=0时,Vague集退化为Fuzzy集.相反1-πA(x)反映了x相对A的确知信息量,1-πA(x)值越大,确知信息量就越多.
2.2 Vague集记分函数
Vague集中记分函数S(x)是用来衡量决策方案对于决策属性要求满足程度的一种衡量标准,是由Chen等人[3]于1994年在讨论Vague集的多准则模糊决策问题时首次提出的.记分函数是Vague集多属性决策的关键和核心,它是Vague集中进行模糊不确定信息集结处理的直接集中与体现.因此,Vague集中记分函数构造的优劣直接影响了Vague集决策的优劣,甚至影响决策结果的正确与否.
3 本文的构造方法
3.1 记分函数涵义分析
为有效构造记分函数,应该将Vague值x=[tx,fx]中tx,fx与πx所包含的信息全面考察分析.其实在Vague值中,确定的信息有2部分:一部分为tx-fx,给出了支持证据与反对证据的偏势∂Δ(优势)[12],∂Δ值越大,S(x)越大;反之,∂Δ值越小,S(x)越小.另一部分为犹豫度πx以外的1-πx,给出了未确知度以外的已确知信息,1-πx越大,已确知信息越多;反之,1-πx越小,已确知信息越少.
在Vague记分函数构造中应包含这2部分信息,但决策者在记分函数构造中经常会出现悲观、中立或乐观等偏好心态,因此在记分函数S(x)构造中还要考虑决策者决策偏好情况及πx在决策偏好时趋向于偏好的程度.为了能够构造有效、合理、准确的Vague记分函数S(x),则S(x)应该满足如下的准则:
准则1:(tx-fx)≥(ty-fy),则S(x)≥S(y);反之亦然.
准则2:乐观决策中,当tx≻fx时,有ΔS(x)≻ΔS(y).
准则3:悲观决策中,当txfx时,有ΔS(x)ΔS(y).
准则4:中立决策中,有ΔS(x)≈ΔS(y).
3.2 本文记分函数
在分析前述Vague记分函数基础上,本文构造了如下记分函数.为表达方便,先定义几个概念.
定义4 对Vague值x=[tx,fx],称H(x)=1-πx为Vague值x的精确度或已确知度.
定义5 对Vague值x=[tx,fx],称∂Δ(x)=tx-fx为Vague值x的偏势或优势.
其实H(x)和∂Δ(x)在Vague集中类似于统计学中的方差和均值概念[13].∂Δ(x)越大,且H(x)越小,则构造记分函数结果越优.
定义6 对Vague值x=[tx,fx],定义记分函数为
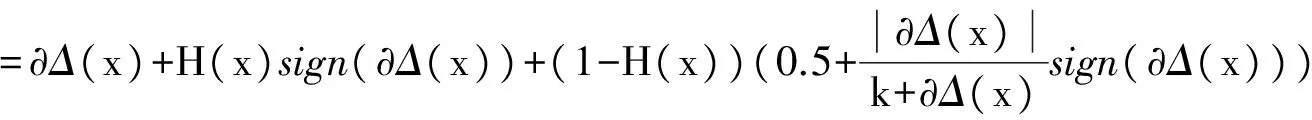
其中k是一个校正参数(k≥1),起到对记分函数结果误差校正作用.在实际计算中,为了计算方便,通常取k=1.
对定义6,其实由3部分组成:
第1部分:∂Δ(x)为偏势部分,与决策偏好无关.
第2部分:H(x)为精确度或已确知度部分.这部分与决策偏好相关,通过函数sign(x)进行不同决策偏好趋向处理.
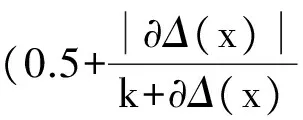
显然定义6记分函数包含了Vague值中tx,fx与πx全部信息在不同决策心态下偏好趋向的总值,同时该记分函数体现决策时少数服从多数的原则和心理学决策中“马太效应”[10].因此定义6记分函数具有适用性和可行性.
从定义6 易知,该记分函数SW(x)满足准则1到准则4的要求.
4 结果比较分析
为便于比较本文构造的记分函数有效性、合理性和可行性,采用文献[10]为例进行分析,结果见表1所示.

表1 本文记分函数与已有相关文献结果比较Tab.1 The comparison results of this paper score function with the existing literatures
从表1可知:
SC(x)记分函数与SZ(x)记分函数没有分辨率,不能区分[0.4,0.6],[0.5,0.5],而SL(x)与SME(x)记分函数虽然能分辨,但其缺点前面已经分析,并且SME(x)记分函数中[0.6,0.8]优于[0.7,0.7]的结论明显有误.本文SW(x)记分函数具有较好的分辨率,它能反映出实际客观和直觉模糊的要求,符合人类思维认知规律.因此SW(x)记分函数是可行的、有效的,并有较好分辨率.
5 结论
本文在分析已有Vague集记分函数的同时,指出了现有记分函数的不足与缺陷,讨论并构造了Vague集记分函数相关准则及涵义,在此基础上,给出了一种新的Vague集记分函数.最后通过实例比较分析了该方法的可行性和有效性.
[1] Zadeh L A. Fuzzy sets[J].Information and Control,1965,8(3):338-357.
[2] Gau W L,Buehrer D J. Vague sets[J].IEEE Transactions on Systems, Man and Cybernetics, 1993,23(2):610-614.
[3] Chen S M, Tan J M. Handling multi-criteria fuzzy decision-making problems based on Vague set theory[J]. Fuzzy Sets and Systems, 1994,67(2):163-172.
[4] Hong D H, Choi C H. Multi-criteria fuzzy decision-making problems based on Vague set theory[J]. Fuzzy Sets and Systems, 2000,114(1):103-113.
[5] 李凡,卢安,蔡立晶.基于Vague集的多目标模糊决策方法[J].华中科技大学学报:自然科学版,2001,29(7):1-3.
[6] 刘华文.多目标模糊决策的Vague集方法[J].系统工程理论与实践,2004,24(5):103-109.
[7] 周珍,吴祈宗,兰晓亭.基于记分函数的区间值Vague集的相似度量[J].小型微型计算机系统,2006,27(6):1001-1012.
[8] 王爱领.基于改进的Vague-Topsis方法的公租房轮候排序评价研究[J].郑州大学学报:理学版,2013,45(3):115-119.
[9] Ye J. Improved method of multi-criteria fuzzy decision-making based on Vague sets[J]. Fuzzy Sets and Systems, 2007,39(2):164-169.
[10]王伟平.基于Vague集的语言型多准则决策方法[M].北京:经济科学出版社,2013:66-68.
[11]虎晓红,钱旭,兰洋.基于Vague融合的自动图像标注方法[J].郑州大学学报:理学版,2010,42(1):41-44.
[12]王万军,李恒杰,胡建军,等.基于Vague值转化Fuzzy值的一种新方法[J].计算机工程与应用,2012,48(36):134-136.
[13]徐泽水.直觉模糊信息集成理论及应用[M].北京:科学出版社,2008:2-5.
A Construction Method Based on Score Function for Vague Sets
WANG Wan-jun
(InformationEngineeringCollege,LanzhouUniversityofArtsandScience,Lanzhou730000,China)
Based on present score function for Vague sets, a new score function was constructed for Vague sets. The method could effectively describe the different risk preference relation, and overcome the defects and shortcomings of the traditional score function. The meaning and criterion of the new structure score function were discussed. Finally, an example was given to analyze the feasibility and effectiveness of the method.
Vague sets; score function; construction method
2013-08-27
甘肃省高等学校研究生导师科研项目,编号1215-04;甘肃省教育厅科研项目,编号1113-01;兰州文理学院科研能力提升计划骨干项目,编号2012GGTS01.
王万军(1974-),男,副教授,主要从事计算机智能信息处理与信息决策分析技术研究,E-mail: wangwanjun1@163.com.
TP 301
A
1671-6841(2014)01-0033-04
10.3969/j.issn/1671-6841.2014.01.008

